Hans Walser, [20100607a]

Schließungsfiguren mit Sternen

1 Beispiele

1.1 Stern mit fünf Spitzen

Wir beginnen mit einem beliebigen Stern mit fünf Spitzen. Dieser kann durchaus in einem Quadratraster liegen, braucht also nicht regelmäßig zu sein.

Stern mit fünf Spitzen

Nun spiegeln wir fortlaufend an jeweils der folgenden Spitze gemäß Figur. Es ergibt sich eine Schließungsfigur mit der Periodenlänge 10.

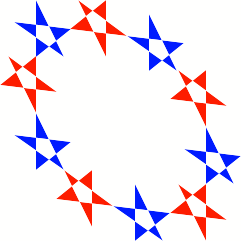
Schließungsfigur

1.2 Stern mit sieben Spitzen

Analog können wir etwa mit einem Stern mit sieben Spitzen verfahren.

Stern mit sieben Spitzen

Es ergibt sich eine Schließungsfigur der Periodenlänge 14.

Schließungsfigur

2 Beweis

2.1 Bezeichnungen

Wir beginnen mit n Punkten und spiegeln diese am Punkt . Die Bildpunkte seien ; es ist also . Nun spiegeln wir die Punkte an und erhalten . Wir fahren entsprechend weiter, also .

Die Abbildung zeigt die Beschriftungssituation der Punkte für .

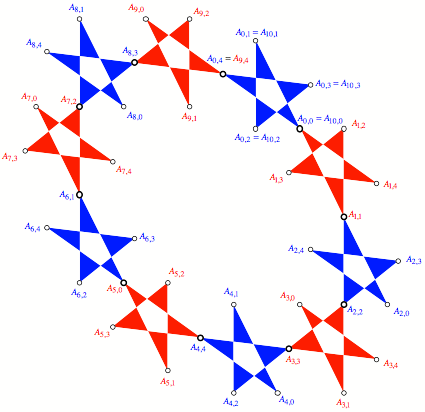
Beschriftungen

2.2 Vektoren

Ferner sei . Als Folge der Punktspiegelungen ist .

Wir untersuchen nun das Polygon:

Für den zugehörigen Vektorzug erhalten wir die Einzelvektoren:

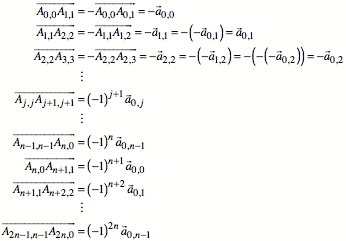
Somit ist:

2.3 Fallunterscheidung

Nun ist eine Fallunterscheidung bezüglich der Parität von n erforderlich.

2.3.1 Ungerade Eckenzahl

Für ungerades n gilt:

Wir haben eine Schließungsfigur der Periodenlänge .

2.3.2 Gerade Eckenzahl

Für gerades n haben wir:

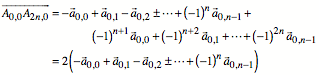
Wir haben eine Schließungsfigur genau dann, wenn:

Dann ist aber bereits:

Die Schließungsfigur hat die Periodenlänge n.

3 Bemerkungen und Beispiele

3.1 Ungerade Eckenzahl

3.1.1 Überlappungen

Wir haben bei ungeradem n immer eine Schließungsfigur der Periodenlänge . Als Basis ist aber nicht eine Sternfigur erforderlich. Es genügt ein Polygon mit n Ecken. Allerdings kann es dabei zu Überlappungen kommen, so dass die Schließungseigenschaft schlecht einsehbar ist. Die Figur zeigt die Situation mit einem konvexen Fünfeck als Basisfigur.

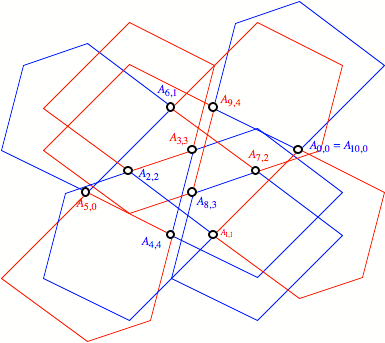
Überlappungen

3.1.2 Punktsymmetrie

Für ungrades n sind die Schließungsfiguren als Ganzes punktsymmetrisch.

Um dies zu beweisen, brauchen wir einen Hilfssatz über die Reduktion von Zusammensetzungen von Punktspiegelungen: Die Zusammensetzung dreier Punktspiegelungen lässt sich als eine einzige Punktspiegelung darstellen: . Dabei ist D die Ergänzung der drei Punkte A, B, C zum Parallelogramm. Daraus folgt, dass sich eine Zusammensetzung von ungerade vielen Punktspiegelungen als eine einzige Spiegelung darstellen lässt. Wir können also schreiben:

Die Punkte werden also mit der Punktspiegelung auf die Punkte abgebildet. Insbesondere ist . Die Ergänzung der Punkte zum Parallelogramm ergibt wiederum den Punkt M. Aus

folgt:

Es werden mit der Punktspiegelung also die Punkte auf die Punkte abgebildet und allgemein die Punkte auf die Punkte . Daher ist M das Symmetriezentrum der Gesamtfigur.

3.2 Gerade Eckenzahl

3.2.1 Bandornament

Aus dem Beweis geht für gerades n hervor:

Wenn also (Regelfall) ist, bilden die Punkte eine äquidistante Punktefolge auf einer Geraden. Durch Fortsetzen unseres Spiegelungsprozesses erhalten wir ein Bandornament. Die Figur zeigt ein Beispiel für .

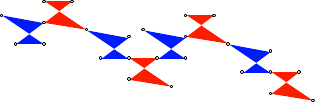
Bandornament

3.2.2 Schließungsfiguren

Eine Schließungsfigur gibt es für gerades n genau dann, wenn:

Da die Vektoren sich zum Basispolygon schließen, gilt auch:

Addition und Subtraktion dieser beiden Gleichungen liefert:

Geometrisch heißt das, dass das Basispolygon sich alternierend aus Vektoren zusammensetzt, welche je ihrerseits ein geschlossenes Polygon bilden. Wir können also aus den Seitenvektoren zweier Polygone mit je Ecken durch alternierende Zusammensetzung das Basispolygon für die Schließungsfigur konstruieren.

3.2.2.1 Parallelogramm

Für haben wir die Bedingung . Das Basispolygon ist ein Parallelogramm. Es ist alternierend aus den Seitenvektoren zweier geschlossener „Zweiecke“ zusammengesetzt.

Schließungsfigur mit Parallelogramm

3.2.2.2 Sechseck

Wir setzen das Sechseck alternierend aus den Seitenvektoren zweier Dreiecke zusammen.

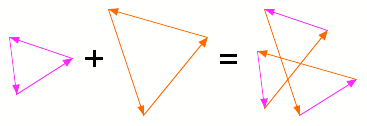
Konstruktion des Sechseckes aus zwei Dreiecken

Mit diesem Sechseck ergibt sich eine Schließungsfigur mit der Periodenlänge sechs.

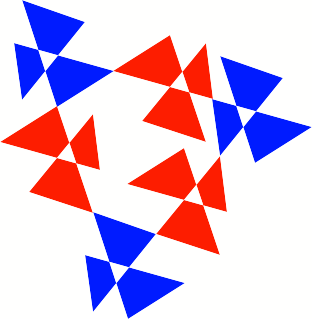
Schließungsfigur mit Periodenlänge sechs

3.2.2.3 Achteck

Wir setzen das Achteck aus zwei Vierecken zusammen.

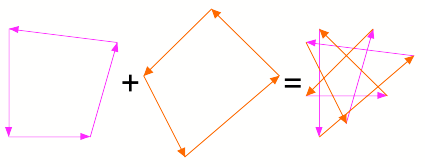
Konstruktion des Achteckes aus zwei Vierecken

Wir erhalten eine Schließungsfigur mit der Periodenlänge acht.

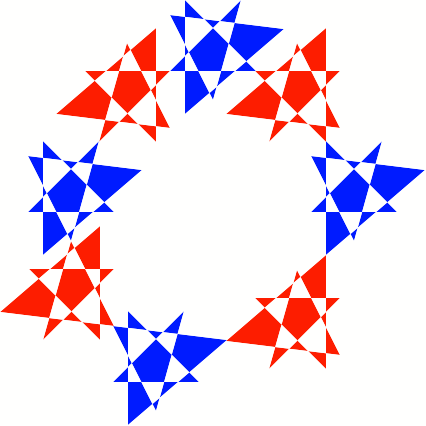
Schließungsfigur mit Periodenlänge acht