Hans Walser, [20221017]

Satz von Stoll

Anregung: Thomas Jahre, Aufgabe 61-726

1 Worum geht

Ein Satz über spezielle Punkte im Viereck. CAS-Beweis

2 Der Satz von Stoll

Im Viereck sind der Diagonalenschnittpunkt G, der Eckenschwerpunkt E und der Flächenschwerpunkt F kollinear (Abb. 1). Es ist GE = 3EF.

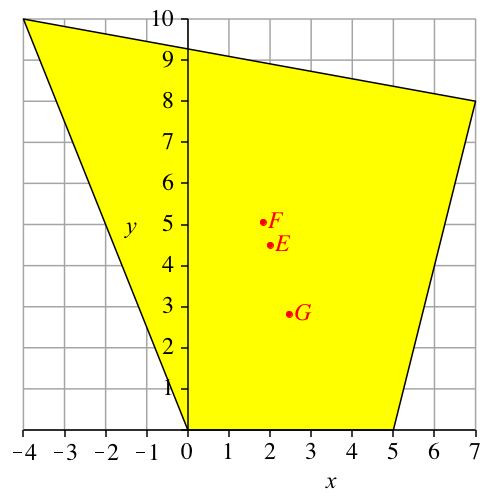
Abb. 1: Der Satz von Stoll

3 Beweis

Rechnerischer Beweis mit CAS.

Das Viereck ABCD habe die Ecken A[xA, yA], B[xB, yB], C[xC, yC], D[xD, yD].

3.1 Schnittpunkt zweier Geraden

Die Gerade AB wird mit der Geraden BC geschnitten.

Maple-Programm

Geradenschnittpunkt := proc(A, B, C, D) local GlgSys, Sol, x, y, Schnittpunkt:

GlgSys := {x*A[1] + (1-x)*B[1] = y*C[1] + (1-y)*D[1], x*A[2] + (1-x)*B[2] = y*C[2] + (1-y)*D[2]}:

Sol := solve(GlgSys, [x,y]):

assign(Sol):

x := x:

y := y:

Schnittpunkt := [x*A[1] + (1-x)*B[1], x*A[2] + (1-x)*B[2]]:

end:

3.2 Diagonalenschnittpunkt

Programm

Diagonalenschnittpunkt := proc(A, B, C, D) local G:

G := Geradenschnittpunkt (A, C, B, D):

end proc:

Output

G := [(((yC - yD)*xB + xD*(yB - yC))*xA - ((yA - yD)*xB - xD*(yA - yB))*xC)/((yB - yD)*xA + (-yA + yC)*xB + (-yB + yD)*xC + xD*(yA - yC)), (((-xC + xD)*yB - yD*(xB - xC))*yA + ((xA - xD)*yB - yD*(xA - xB))*yC)/((-xB + xD)*yA + (xA - xC)*yB + (xB - xD)*yC - yD*(xA - xC))]

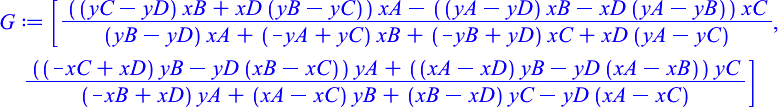
3.3 Eckenschwerpunkt

Programm

Eckenschwerpunkt := proc(A, B, C, D) local E:

E := 1/4*(A + B + C + D):

end proc:

Output

E := [xD/4 + xC/4 + xB/4 + xA/4, yD/4 + yC/4 + yB/4 + yA/4]

3.4 Flächenschwerpunkt

Das Vorgehen ist folgendes.

Die Schwerpunkte der Dreiecke ABD und BCD werden durch eine Gerade verbunden.

Die Schwerpunkte der Dreiecke ABC und ACD werden durch eine Gerade verbunden.

Der Schnittpunkt der beiden Geraden ist der Flächenschwerpunkt.

Programm

Flaechenschwerpunkt := proc(A, B, C, D) local ABC, ABD, ACD, BCD , Flaechenschwerpunkt :

ABC := 1/3*(A + B + C):

ABD := 1/3*(A + B + D):

ACD := 1/3*(A + C + D):

BCD := 1/3*(B + C + D):

Flaechenschwerpunkt := Geradenschnittpunkt (ABD, BCD, ABC, ACD):

end proc:

Output

F := [((yB - yD)*xA^2 + ((-yA + yB)*xB + xD*(yA - yD))*xA + (-yA + yC)*xB^2 - xC*(yB - yC)*xB + (-yB + yD)*xC^2 - xD*(yC - yD)*xC + xD^2*(yA - yC))/((3*yB - 3*yD)*xA + (-3*yA + 3*yC)*xB + (-3*yB + 3*yD)*xC + 3*xD*(yA - yC)), ((-xB + xD)*yA^2 + ((xA - xB)*yB - yD*(xA - xD))*yA + (xA - xC)*yB^2 + yC*(xB - xC)*yB + (xB - xD)*yC^2 + yD*(xC - xD)*yC - yD^2*(xA - xC))/((-3*xB + 3*xD)*yA + (3*xA - 3*xC)*yB + (3*xB - 3*xD)*yC - 3*yD*(xA - xC))]

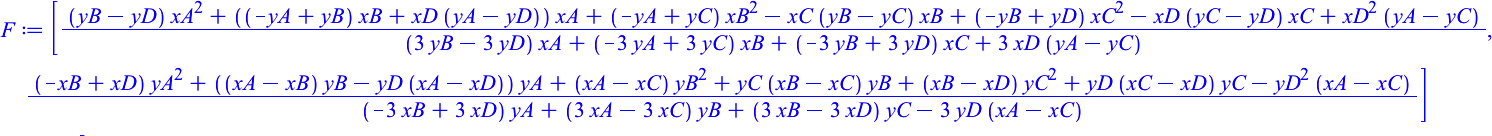
Die Formel ist recht kompliziert.

3.5 Beweis des Satzes von Stoll

Wir haben zu zeigen: GE = 3EF. Dies ist äquivalent mit (E – G) – 3*(F – E) = 0 (Nullvektor).

Programm

Beweis := (E - G) - 3*(F - E);

Output

Beweis := [-3*((yB - yD)*xA^2 + ((-yA + yB)*xB + xD*(yA - yD))*xA + (-yA + yC)*xB^2 - xC*(yB - yC)*xB + (-yB + yD)*xC^2 - xD*(yC - yD)*xC + xD^2*(yA - yC))/((3*yB - 3*yD)*xA + (-3*yA + 3*yC)*xB + (-3*yB + 3*yD)*xC + 3*xD*(yA - yC)) - (((yC - yD)*xB + xD*(yB - yC))*xA - ((yA - yD)*xB - xD*(yA - yB))*xC)/((yB - yD)*xA + (-yA + yC)*xB + (-yB + yD)*xC + xD*(yA - yC)) + xD + xC + xB + xA, -3*((-xB + xD)*yA^2 + ((xA - xB)*yB - yD*(xA - xD))*yA + (xA - xC)*yB^2 + yC*(xB - xC)*yB + (xB - xD)*yC^2 + yD*(xC - xD)*yC - yD^2*(xA - xC))/((-3*xB + 3*xD)*yA + (3*xA - 3*xC)*yB + (3*xB - 3*xD)*yC - 3*yD*(xA - xC)) - (((-xC + xD)*yB - yD*(xB - xC))*yA + ((xA - xD)*yB - yD*(xA - xB))*yC)/((-xB + xD)*yA + (xA - xC)*yB + (xB - xD)*yC - yD*(xA - xC)) + yD + yC + yB + yA]

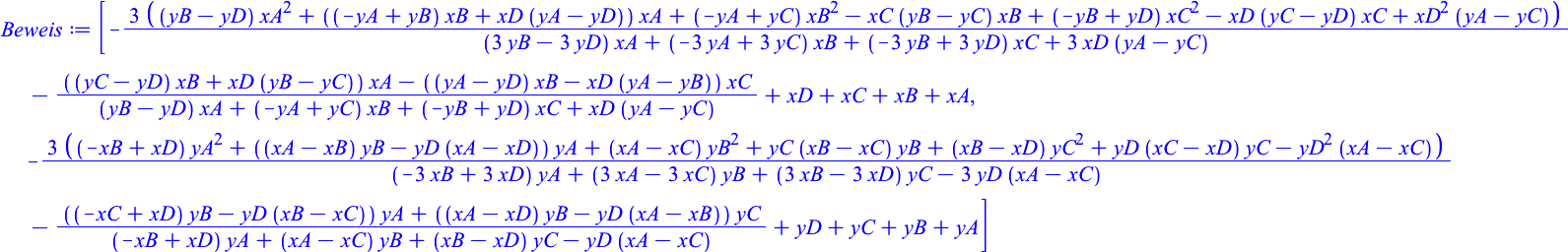
Das sollte der Nullvektor sein. — Eine Frage von Termumformungen.

Programm

Beweis := simplify((E - G) - 3*(F - E));

Output

Beweis := [0, 0]

Schön. Damit ist der Satz von Stoll bewiesen.

4 Nochmals das Beispiel

Beispiel der Abbildung 1 mit exakten und numerischen Koordinatenangaben gemäß den obigen Formeln.

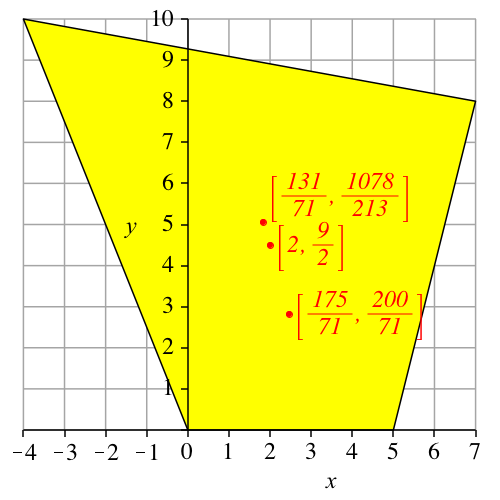
Abb. 2: Exakte Koordinaten

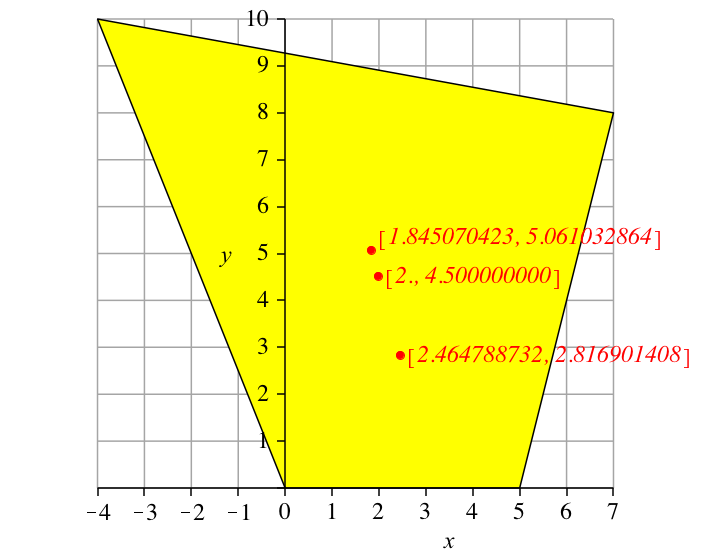
Abb. 3: Gerundete Dezimalwerte

Literatur

Fritsch, Rudolf (2012): Zum Flächenschwerpunkt für Vierecke. Der mathematische und natur-wissenschaftliche Unterricht 65, 2012, S. 464–465.

Fritsch, Rudolf und Pickert, Günter (2014): Schwerpunkte von Vierecken. Die Wurzel, Heft 2 / 2014, 35-41.

Kirsch, A. (1987): Bemerkungen zum Vierecksschwerpunkt. Didaktik der Mathematik, 15, 34-36.

Kratz, Johannes (1994): „Das Schwerpunktsviereck“ – Eine Ergänzung zum Beitrag von Karl Seebach über Viereckschwerpunkte. Didaktik der Mathematik 22, 1994, S. 316–317.

Pickert, Günter (2013): Zu: Zum Flächenschwerpunkt für Vierecke. Der mathematische und naturwissenschaftliche Unterricht 66, 2013, Seiten 51–52.

Seebach, K. (1983/84): Über Schwerpunkte von Dreiecken, Vierecken und Tetraedern. Teil 1: Didaktik der Mathematik 11, 1983, 270-282. Teil 2: Didaktik der Mathematik 12, 1984, 36-44.

Seebach, K. (1994): Nochmals Viereckschwerpunkte. Didaktik der Mathematik, 22, 309-315.

Seebach, Karl (1983): Über Schwerpunkte von Dreiecken, Vierecken und Tetraedern, Teil 1. Didaktik der Mathematik 11, 1983, S. 270–282.

Seebach, Karl (1994): Nochmals: Viereckschwerpunkte. Didaktik der Mathematik 22, 1994, S. 309–315.

Stoll, E. (1880): Ueber den Schwerpunkt des Vierecks. In: Archiv Math. Phys. (Grunerts Archiv) 65 (1880), S. 445 f.

Walser, H. (2012): Schwerpunkt. Mathematikinformation, 57, 14-22. ISSN 1612-9156.

Walser, Hans (2014): Flächenschwerpunkte. MNU, Der mathematische und naturwissenschaftliche Unterricht. 67. Dezember 2014, S. 466-467.