Hans Walser, [20210620]

Rotationskörpervolumina

1 Worum geht es?

Volumina einiger Rotationskörper im Umfeld der Einheitskugel.

Eine Fleißarbeit

2 Beispiele

2.1 Einheitskugel

Abb. 2.1: Einheitskugel

Beim Achsenschnitt sehen wir in die Kugel hinein. Die Schnittebene ist die x,z-Ebene.

Abb. 2.1: Einheitskugel, Achsenschnitt

(2.1)

2.2 Zylinder

Boden und Deckel sind nicht gezeichnet, um den Blick auf die innenliegende Einheitskugel freizulassen.

Abb. 2.2: Zylinder

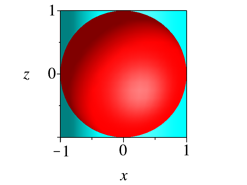
Abb. 2.2: Zylinder, Achsenschnitt

(2.2)

2.3 Kegel

2.3.1 Standardkegel

Die Meridiankurve ist eine Gerade.

Abb. 2.3.1: Standardkegel

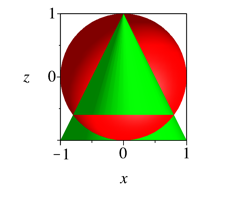
Abb. 2.3.1: Standardkegel, Achsenschnitt

(2.3.1)

2.3.2 Doppelkegel

Abb. 2.3.2: Doppelkegel

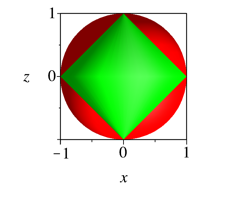
Abb. 2.3.2: Doppelkegel, Achsenschnitt

(2.3.2)

2.3.3 Tordierter Doppelkegel

Abb. 2.3.3a: Tordierter Doppelkegel

Der Begriff Achsenschnitt ist beim tordierten Doppelkegel nicht anwendbar.

Abb. 2.3.3b: Tordierter Doppelkegel

(2.3.3)

Wir haben bei allen Kegeln dasselbe Volumen.

2.4 Paraboloide

2.4.1 Standard-Rotationsparaboloid

Die Meridiankurve ist eine stehende Parabel.

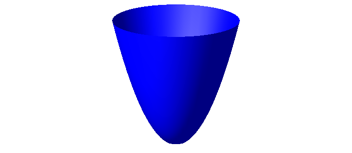
Abb. 2.4.1: Rotationsparaboloid

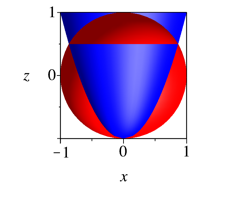
Abb. 2.4.1: Rotationsparaboloid, Achsenschnitt

(2.4.1)

2.4.2 Doppelparaboloid

Die Meridiankurve setzt sich aus einer stehenden nach oben offenen Parabel und einer stehenden nach unten offenen Parabel zusammen.

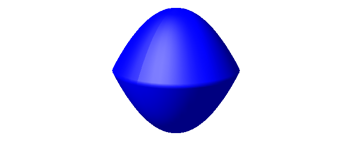
Abb. 2.2.4: Doppelparaboloid

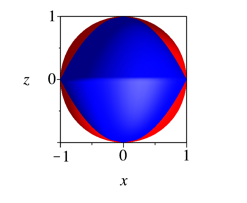
Abb. 2.4.2: Doppelparaboloid, Achsenschnitt

(2.4.2)

2.4.3 Parabelspindel

Die Meridiankurve ist eine liegende Parabel.

Abb. 2.4.3: Parabelspindel

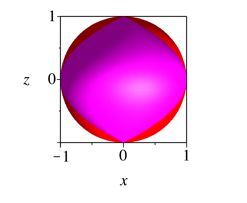
Abb. 2.4.3: Parabelspindel, Achsenschnitt

(2.4.3)

2.5 Kosinus-Flächen

2.5.1 Kosinusspindel

Die Meridiankurve ist eine gestauchte und um 90° gedrehte Kosinuskurve.

Abb. 2.5.1a: Kosinusspindel gestaucht

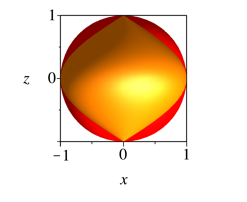
Abb. 2.5.1a: Kosinusspindel gestaucht, Achsenschnitt

(2.5.1a)

Bei der ungestauchten Parabel haben wir eine um 90° gedrehte Kosinuskurve als Meridian.

Abb. 2.5.1b: Kosinusspindel ungestaucht

Die Einheitskugel ist Schmiegungskugel am Äquator. Daher das unscharfe Bild.

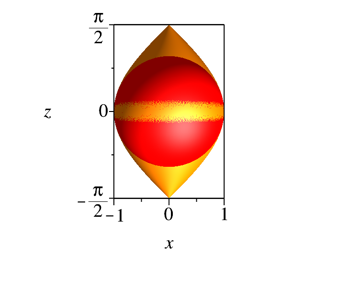
Abb. 2.5.1b: Kosinusspindel ungestaucht, Achsenschnitt

(2.5.1b)

2.5.2 Kosinusscheibe

Die Meridiankurve setzt sich aus in der Längsrichtung gestauchten Kosinuskurven zusammen.

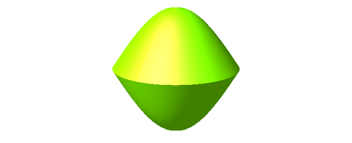
Abb.2.5.2a: Kosinusscheibe gestaucht

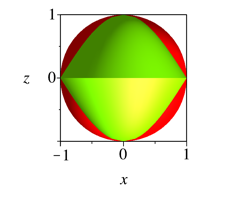
Abb. 2.5.2a: Kosinusscheibe gestaucht, Achsenschnitt

(2.5.2a)

Bei der ungestauchten Kosinusscheibe setzt sich die Meridiankurve aus gewöhnlichen Kosinuskurven zusammen.

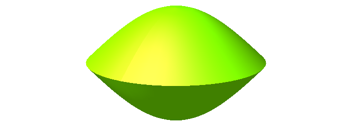
Abb. 2.5.2b: Kosinusscheibe ungestaucht

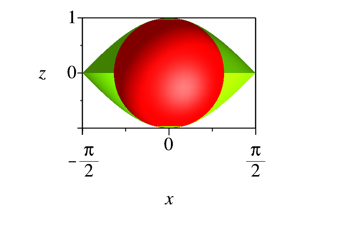
Abb. 2.5.2b: Kosinusscheibe ungestaucht, Achsenschnitt

(2.5.2b)

2.6 Rotationshyperboloid

Die Meridiankurve ist eine gleichseitige Hyperbel. Der Kehlkreis ist der Einheitskreis.

Abb. 2.6a: Rotationshyperboloid

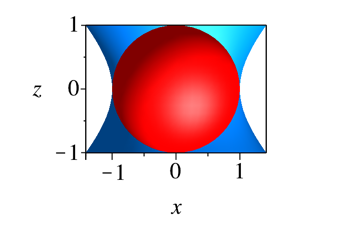
Abb. 2.6a: Rotationshyperboloid, Achsenschnitt

(2.6a)

Beim gestauchten Hyperboloid sind die Kreise auf den Niveaus ±1 Einheitskreise.

Abb. 2.6b: Hyperboloid gestaucht

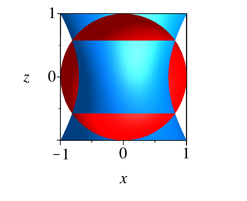
Abb. 2.6b: Hyperboloid gestaucht, Achsenschnitt

(2.6b)