Hans Walser, [20141216]
Ršsselsprung-Metrik
1 Worum geht es?
Wir definieren den Abstand zweier Felder im Schachbrett durch die minimale Anzahl von Ršsselsprźngen mit denen das zweite Feld vom ersten Feld aus erreicht werden kann.
Die Abbildung 1.1 zeigt den ăEinheitskreisŇ.
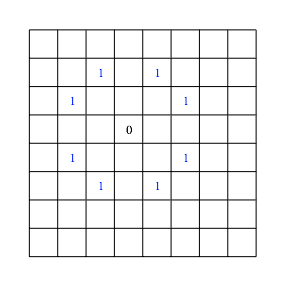
Abb. 1.1: Einheitskreis
In der Abbildung 1.2 sind auch die Felder markiert, welche vom Ursprungsfeld aus in zwei Ršsselsprźngen erreicht werden kšnnen. Wir sehen, dass die Welt des Schachbrettes bereits zu klein ist.

Abb. 1.2: Abstand 2
2 Codierte Darstellung
Wir verzichten im Folgenden auf das Zeichnen des Schachbrettes und codieren die Felder farblich nach dem Abstand vom Ursprungsfeld. Dazu schreiben wir den Abstand im Dualsystem und codieren entsprechend im RGB-System (Tab. 1).
|
Abstand |
Dualzahl |
RGB |
Farbe |
|
|
0 |
000 |
RGB(0,0,0) |
schwarz |
|
|
1 |
001 |
RGB(0,0,1) |
blau |
|
|
2 |
010 |
RGB(0,1,0) |
grźn |
|
|
3 |
011 |
RGB(0,1,1) |
zyan |
|
|
4 |
100 |
RGB(1,0,0) |
rot |
|
|
5 |
101 |
RGB(1,0,1) |
magenta |
|
|
6 |
110 |
RGB(1,1,0) |
gelb |
|
|
7 |
111 |
RGB(1,1,1) |
wei§ |
|
Tab. 1: Farbcodierung
Die Abbildungen 2 zeigen der Reihe nach die Codierungen fźr die AbstŠnde 0 bis 6.
![]()
Abb. 2.0: Ursprungsfeld

Abb. 2.1: Einheitskreis

Abb. 2.2: Abstand 2
Die ă†bereck-FelderŇ haben also den Abstand 2.

Abb. 2.3: Abstand 3
Benachbarte Felder haben den Abstand 3.

Abb. 2.4: Abstand 4

Abb. 2.5: Abstand 5

Abb. 2.6: Abstand 6
3 Minimalwege
Wir zŠhlen nun die kźrzesten Wege zwischen zwei Feldern mit gegebenem Abstand.
Fźr den Abstand 1 gibt es nur einen Minimalweg (Abb. 3.1).
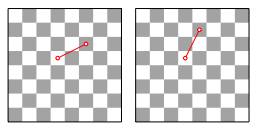
Abb. 3.1: Minimalweg
Die Abbildung 3.2 zeigt modulo die Symmetriegruppe des Quadrates alle mšglichen Beispiele fźr den Abstand 2. Wir haben einen oder zwei Wege. Als Figuren kommen Strecke, Rhombus und Quadrat vor.
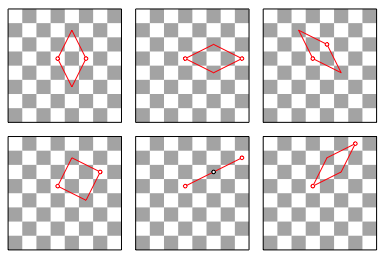
Abb. 3.2: Minimalwege bei Abstand 2
Die Abbildung 3.3 zeigt modulo die Symmetriegruppe des Quadrates alle mšglichen Beispiele fźr den Abstand 3. Die Anzahlen der Minimalwege sind 1, 3, 6, 9 oder 12.Als Figuren erscheinen Strecke, Zusammensetzung zweier Rhomben oder Quadrate, und Wźrfel sowie Kombinationen davon.

Abb. 3.3: Minimalwege bei Abstand 3
Die Abbildung 3.4 zeigt einige Beispiele fźr den Abstand 4. Die Strecke der LŠnge 4 hat nicht Platz im Schachbrett. Im letzten Beispiel sehen wir einen vierdimensionalen Wźrfel. Der Autor ist nicht sicher, ob alle Beispiele vollstŠndig sind.
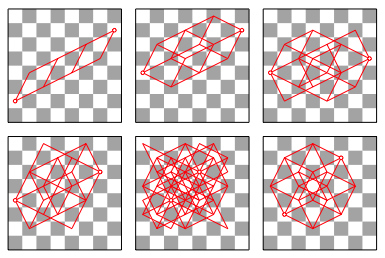
Abb. 3.4: Einige Beispiele zum Abstand 4