Hans Walser, [20161017]
Reflexion an Kugel
Idee und Anregung: W. K., F.
1 Worum geht es?
Im Innenhof eines Wiener Hotels sind reflektierende Kugeln aufgehngt (Abb. 1).

Abb. 1: Reflektierende Kugeln
Die Abbildung 2 zeigt das Spiegelbild des Innenhofes auf der Kugel in der Bildmitte der Abbildung 1.

Abb. 2: Spiegelbild des Innenhofes
Welchen Anteil des Innenhofes sehen wir im Spiegelbild?
2 Analyse
Wir schneiden die Kugel mit der Ebene durch einen beliebigen Raumpunkt P, den Kugelmittelpunkt M und den Okularpunkt O (Abb. 3).
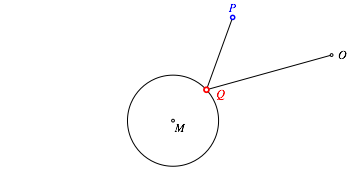
Abb. 3: Ebener Schnitt
Die Konstruktion des Reflexionspunktes Q auf der Kugeloberflche ist ein Thema fr sich. Ich habe mit einer Einschiebe-Lsung gearbeitet.
Die Abbildung 4 zeigt in grau den nicht einsehbaren Raum. Dies ist ein Kegelstumpf.
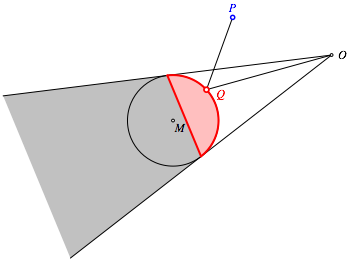
Abb. 4: Nicht einsehbarer Raum
Der Reflexionspunkt liegt auf einer Kugelkalotte (rot), welche den Kegelstumpf oben abschlie§t.
Allerdings sehen wir vom Okularpunkt O aus das Spiegelbild des Rumpunktes P eher auf einer Kreisscheibe, welche die Kugelkalotte unten abschlie§t (Punkt R). Das Spiegelbild des einsehbaren Raumes ist also auf dieser Kreisscheibe sichtbar (Abb. 5).
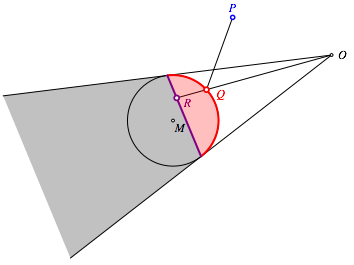
Abb. 5: Kreisfrmiger Bildschirm
3 Der Trick von Newton
Wenn wir die Kugel verkleinern, wird auch der nicht einsehbare Raum kleiner. Allerdings wird dann auch die Kreisscheibe kleiner. Wir sehen mehr von der Welt auf einem kleineren Bildschirm.
Aber wir knnen ja den Bildschirm als Artefakt entsprechend vergr§ern. Dies ist der Trick von Newton: Wir lassen den Kugelradius r gegen null gehen und vergr§ern den kleiner werdenden Bildschirm mit dem Faktor 1/r. Damit bleibt er in handlicher Gr§e. Der nicht einsehbare Raum geht bei diesem Verfahren auch gegen null. Das war ja der Sinn der bung.
Im Grenzfall haben wir das ganze Universum auf einer Kreisscheibe. Die Kugelkalotte wird zur Halbkugel, die Kreisscheibe zu einer Gro§kreisscheibe.
4 Beispiele
4.1 Wrfel und Wrfelgitter
Wir setzen die infinitesimal kleine reflektierende Kugel in die Wrfelmitte. Der Okularpunkt O sei senkrecht oberhalb. In der Abbildung 6 sind je vier parallele Wrfelkanten in gleicher Farbe gezeichnet.
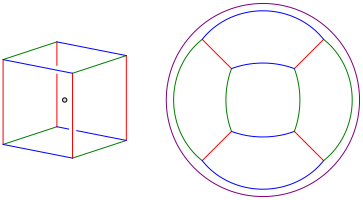
Abb. 6: Bild des Wrfels
Die Abbildung 7 zeigt die Situation mit einem 3×3×3-Wrfelgitter.
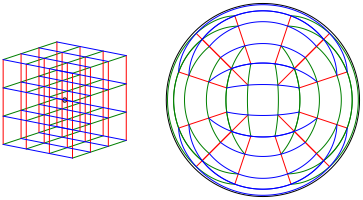
Abb. 7: Wrfelgitter
4.2 Kartografie
Wir denken uns die Erdkugel transparent mit unserer infinitesimal kleinen reflektierenden Kugel im Erdmittelpunkt. Der Okularpunkt sei im Nordpol oder irgendwo auf der oberen Erdachse. Dann sehen wir die Erde im Spiegel gem§ Abbildung 8. Bei dieser Spiegelprojektion wird doppelt gespiegelt: Zunchst sehen wir die Erde von innen spiegelbildlich, und dann wir an der infinitesimalen Kugel ein zweites Mal gespiegelt. Daher entspricht die Orientierung der Karte unseren Gewohnheiten, der Sicht von au§en.
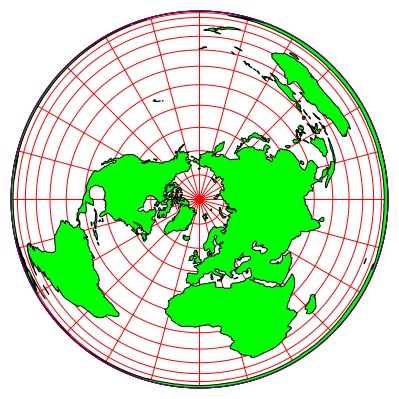
Abb. 8: Spiegelbild der Erdkugel
Diese Erdkugeldarstellung ist ein so genannte Azimutalkarte und flchenverhltnistreu (Azimuthal Equal Area). Die Flchenverhltnisse sind auf der Karte gleich gro§ wie in Wirklichkeit.
Wir sehen die ganze Erdkugel. Am u§ersten Rand ist die Antarktis erkennbar.
Die Abbildung 9 zeigt die Situation mit dem Okularpunkt im Punkt mit den geografischen Koordinaten (0¡N / 0¡E).
Die Lage der beiden Pole ist symmetrisch.
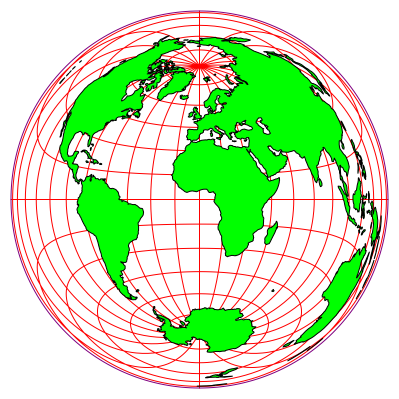
Abb. 9: Okular bei (0¡N / 0¡E)
Die Abbildung 10 schlie§lich zeigt die Situation mit dem Okular in Feldmeilen.
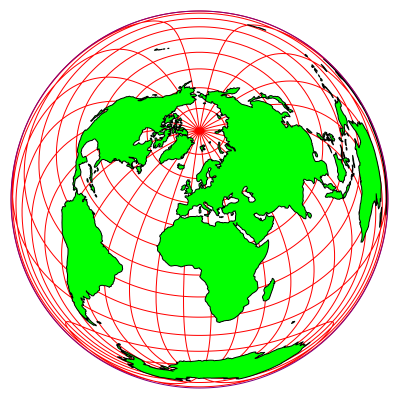
Abb. 10: Okular in Feldmeilen
5 Formeln
Der Raumpunkt P habe die kartesischen Koordinaten (x, y, z). Die infinitesimal kleine reflektierende Kugel sei im Koordinatenursprung und der Okularpunkt auf der positiven z-Achse.
Fr die
Bildschirm-Kreisscheibe verwenden wir die kartesischen Koordinaten ![]() .
.
In dieser Disposition gelten die Abbildungsgleichungen:
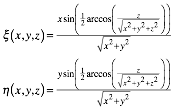 (1)
(1)
Websites
Kartenprojektionen (17.10.2016):
http://swai.ethz.ch/swaie/MapProjector/MapProjector.de.html