1 Worum geht es?

Spiralförmige Unterteilung eines beliebigen Rechtecks in rechtwinkligen Dreiecken.

2 Beispiele

Mit vier rechtwinkligen Dreiecken mit dem Kathetenverhältnis 2:1 können wir ein Goldenes Rechteck (Abb. 1a) auslegen (Walser 2013a, S. 53). Die blauen und die roten Dreiecke sind unterschiedlich orientiert. Im Innern bleibt ein Loch, das ebenfalls das Seitenverhältnis des Goldenen Schnittes hat.

Mit vier rechtwinklig-gleichschenkligen Dreiecken ergibt sich das sogenannte Silberne Rechteck (Abb. 1b) (Walser 2013a, S. 116, Walser 2013b, S. 63-71). Das Loch im Innern ist ebenfalls ein silbernes Rechteck.

Mit vier Dreiecken im Seitenverhältnis 3:4:5 ergibt sich ein Rechteck im Seitenverhältnis 2:1. Es handelt sich hier um pythagoreische Dreiecke. Das Loch im Innern hat ebenfalls das Seitenverhältnis 2:1.

Abb. 1: Beispiele

Wir können nun die Löcher im Innern mit entsprechenden Figuren füllen. Durch Iteration entstehen eckige logarithmische Spiralen (Abb. 2).

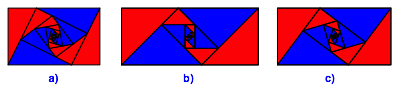
Abb. 2: Eckige logarithmische Spiralen

Man beachte, dass die blauen Spiralen anders aufgebaut sind als die roten.

3 Beliebige rechtwinklige Dreiecke

Wir können mit beliebigen rechtwinkligen Dreiecken ein Rechteck auslegen. Das Loch in der Mitte ist ähnlich zum Außenrechteck. Wir können daher mit Spiralen unterteilen.

Diese Unterteilung funktioniert auch bei „langen“ Rechtecken (Abb. 3). Die Spiralen sind allerdings kaum mehr zu erkennen.

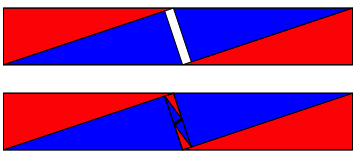
Abb. 3: „Langes“ Rechteck

4 Umkehrung

Die Frage ist, wie wir umgekehrt zu einem gegebenen Rechteck die vier passenden rechtwinkligen Dreiecke finden. Dazu Verfahren wir wie folgt.

Abb. 4: Ausgehend vom Rechteck

Wir zeichnen eine Diagonale und dazu die Mittelsenkrechte (Abb. 4a). Der Schnittpunkt der Mittelsenkrechten mit einer Rechteckseite ist eine der gesuchten Dreiecksecken. Die beiden anderen Dreiecksecken sind die anliegenden Eckpunkte des Rechteckes. Damit haben wir genügend Information, um die vier Dreiecke zu zeichnen (Abb. 4b). Schließlich können wir unterteilen (Abb. 4c). Die blauen und die roten Dreiecke sind unterschiedlich orientiert.

5 Quadrat

Das Verfahren funktioniert bei einem Quadrat nicht. Wir erhalten als Grenzlage ein rechtwinkliges Dreieck, das nur aus einer Strecke besteht.

Bei einem Quadrat sind andere Unterteilungen gebräuchlich (Abb. 5). Es werden ebenfalls rechtwinklige Dreiecke verwendet, diese sind aber alle gleich orientiert. Wir haben es wiederum mit eckigen logarithmischen Spiralen zu tun.

Die drei Beispiele der Abbildung 5 unterscheiden sich nur in der „Auflösung“. Je gröber die rechtwinkligen Dreiecke, umso weniger sind die Spiralen erkennbar.

Abb. 5: Unterteilungen des Quadrates

Literatur

Walser, H. (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.

Walser, H. (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.

Websites

Hans Walser: Pythagoreische Dreiecke

http://www.walser-h-m.ch/hans/Miniaturen_Uebersicht/index.html