Hans Walser, [20190203]

Rationale Seitenverhältnisse

1 Worum geht es?

Wir untersuchen gleichschenklige Dreiecke mit rationalen Seitenverhältnissen. Durch Vervielfachung der Basiswinkel erhalten wir wiederum ein gleichschenkliges Dreieck mit rationalen Seitenverhältnissen.

2 Beispiel

Wir beginnen mit dem Dreieck mit dem Seitenverhältnis 5:5:9 (Abb. 1.1).

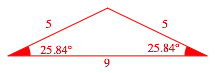
Abb. 1.1: Seitenverhältnis 5:5:9

Für die Basiswinkel erhalten wir:

(1)

Nun das Dreieck mit dem Seitenverhältnis 25:25:31 (Abb. 1.2).

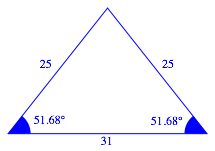
Abb. 1.2: Seitenverhältnis 25:25:31

Für die Basiswinkel erhalten wir:

(2)

Dies ist exakt das Doppelte von (1). Um dies einzusehen verwenden wir das Additionstheorem:

(3)

Es ist dann:

(4)

Nun weiter mit dem Seitenverhältnis 125:125:54 (Abb. 1.3). Der Basiswinkel (1) hat sich nun verdreifacht.

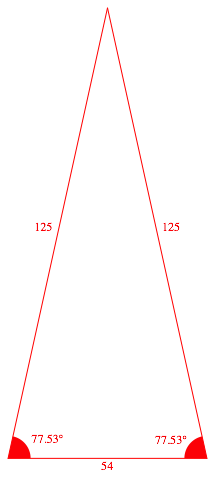
Abb.1.3: Seitenverhältnis 125:125:54

Beim Vervierfachen des Seitenwinkels entsteht ein stumpfer Winkel (Abb. 1.4). Mit einem stumpfen Basiswinkel können wir eigentlich kein gleichschenkliges Dreieck bauen. Mit einer Orientierungsumkehr geht es trotzdem (Abb. 1.4). Für die Basislänge verwenden wir die negative ganze Zahl –289.

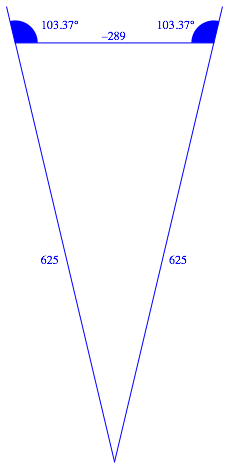
Abb. 1.4: Seitenverhältnis 625:625:–289

Es ist analog zu den obigen Beispielen:

(5)

Und noch ein weiteres Beispiel (Abb. 1.5).

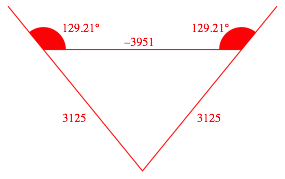
Abb. 1.5: Seitenverhältnis 3125:3125:–3951

Die Abbildung 2 zeigt die Überlagerung der fünf Beispiele auf standardisierter Basis. Wir sehen die lineare Zunahme der Basiswinkel.

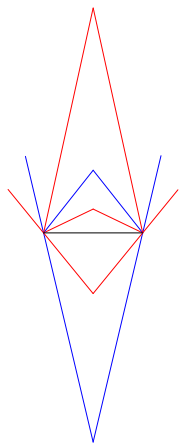
Abb. 2: Überlagerung

3 Formales

Für die Basiswinkel gilt:

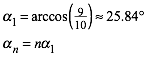(6)

Für die Schenkellängen arbeiten wir mit Potenzen von 5.

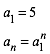(7)

Für die Basislängen arbeiten wir mit der Formel:

(8)

Erstaunlich ist natürlich, dass das „aufgeht“, das heißt immer eine ganze Zahl liefert.

Die Tabelle 1 liefert die ersten Werte.

n
1	5	9
2	25	31
3	125	54
4	625	–289
5	3125	–3951
6	15625	–28334
7	78125	–156231
8	390625	–697729
9	1953125	–2373786
10	9765625	–3920849
11	48828125	24057009
12	244140625	314534306
13	1220703125	2229383529
14	6103515625	12201094111
15	30517578125	54075258774

Tab. 1: Erste Werte

Bemerkung: die Folge ist eine verallgemeinerte Fibonacci- oder Lucas-Folge mit der Rekursion:

(9)

Über Fibonacci-Folgen siehe Walser 2012.

Ein weiteres Beispiel wird in [1] besprochen.

4 Allgemein

Wir beginnen mit einem gleichschenkligen Dreieck der Schenkellänge und der Basislänge . Dieses Dreieck hat den Basiswinkel:

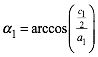(10)

Der Kosinus des Basiswinkels ist also rational. Dann ist auch der Kosinus des n-fachen des Basiswinkels rational. Um dies einzusehen, verwenden wir die Formel von de Moivre:

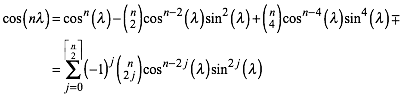(11)

Wegen

(12)

ist mit rationalem Kosinus auch das Quadrat des Sinus rational (der Sinus selber in der Regel nicht).

Da in (11) nur gerade Potenzen des Sinus vorkommen, ist bleibt alles rational. Ein gleichschenkliges Dreieck mit dem Basiswinkel hat also ein rationales Seitenverhältnis. Durch Erweitern mit (Nenner des Bruches in (10) beachten!) erhält man ganzen Zahlen.

Somit Formelsatz:

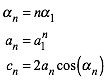(13)

Auf Grund einiger Beispiele vermute ich, dass die Folge die Rekursion hat:

(14)

Für den Beweis konstruieren wir die (verallgemeinerte) Formel von Binet für die Folge mit der Rekursion (14). Diese Formel hat die Form:

(15)

Dabei sind und die Lösungen der quadratischen Gleichung:

(16)

Die Koeffizienten p und q ergeben sich aus den Startwerten der Folge. Die Gleichung (16) hat die Lösungen:

(17)

Wegen ist der Radikand in (17) negativ. Wir haben also zwei konjugiert komplexe Lösungen:

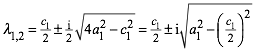(18)

Abb.3: Im Startdreieck

Aus der Abbildung 3 sehen wir, dass wir (18) in der Form schreiben können:

(19)

Damit ergibt sich aus (15):

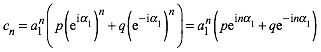(20)

Für p = q = 1 fällt der Imaginärteil in (20) weg und es bleibt übrig:

(21)

Dies entspricht dem Formelsatz (13).

Weblinks

[1] Hans Walser: Wurzel-2-Dreieck:

www.walser-h-m.ch/hans/Miniaturen/W/Wurzel-2-Dreieck/Wurzel-2-Dreieck.htm

Literatur

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.