Hans Walser, [20230306]

Quadratspirale

1 Worum geht es?

Aus Quadraten aufgebaute eckige logarithmische Spiralen.

2 Konstruktionsvorgang

Wir beginnen mit einem Quadrat (Abb. 1).

Abb. 1: Startquadrat

Diesem Quadrat setzen wir übereck ein zweites, mit dem Faktor f gestrecktes Quadrat an (Abb. 2 mit f = 0.7).

Abb. 2: Quadrat ansetzen

Entsprechend können wir ein weiteres Quadrat ansetzen (Abb. 3).

Abb. 3: Weiteres Quadrat ansetzen

3 Spirale

Iteration führt zu einer eckigen logarithmischen Spirale (Abb. 4 und 5).

Abb. 4: Spirale

Abb. 5: Spirale

4 Variation des Streckfaktors

Für f = 1 ergibt sich eine geschlossene Kreuzfigur (Abb. 6).

Abb. 6: Schließungsfigur

Für f = 0.9 überlappt sich die Spirale (Abb. 7).

Abb. 7: Selbstüberlappung

In der Abbildung 8 variiert der Streckfaktor f zwischen 0.4 und 1. Die Abbildung ist so organisiert, dass das Zentrum der Spiralen invariant bleibt. Man kann den Mauszeiger dort drauf tun, um das zu kontrollieren.

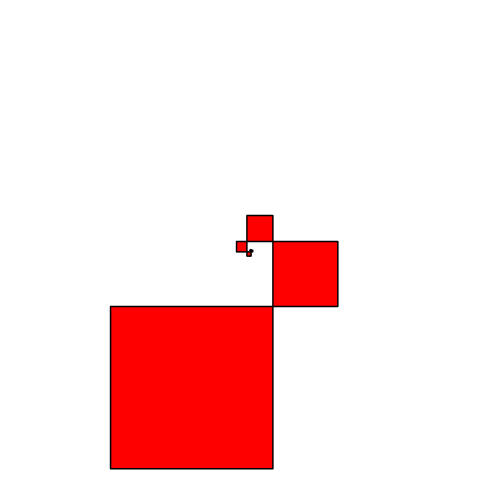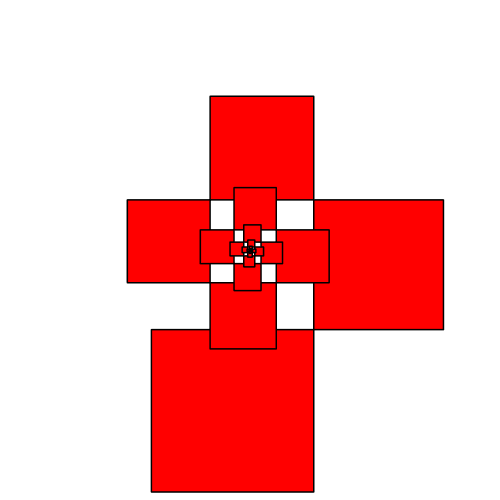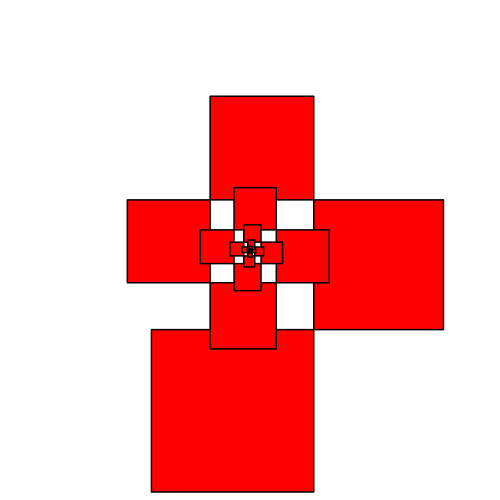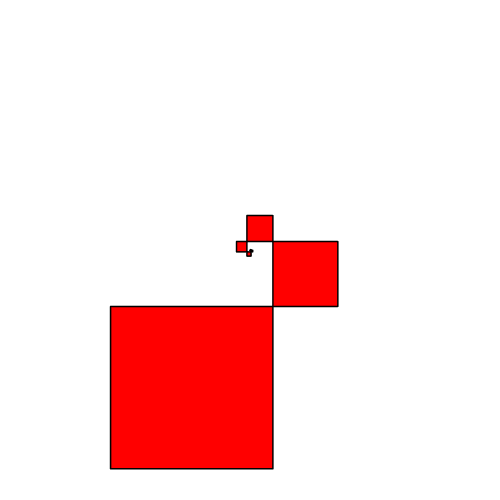
Abb. 8: Variation des Streckfaktors

5 Grenzfall

Für welchen Wert des Streckfaktors f ergibt sich weder eine Selbstüberlappung (Abb. 7) noch einen Zwischenraum (Abb. 5)?

Die Abbildungen 9 und 10 zeigen diesen Grenzfall.

Abb. 9: Grenzfall

Abb. 10: Grenzfall

Zur Berechnung des Streckfaktors f für diesen Grenzfall orientieren wir uns an der Abbildung 11.

Abb. 11: Berechnung des Streckfaktors

Wir lesen die Bedingung ab:

Wegen f ≠ 0 kann diese Bedingung vereinfacht werden zu:

Diese kubische Gleichung für f hat die reelle Lösung:

Dies ist der gesuchte Streckfaktor.

6 Mehrere Runden

6.1 Zwei Runden

In der Spirale der Abbildungen 12 und 13 sitzt das Quadrat erst nach zwei Runden auf dem Startquadrat auf.

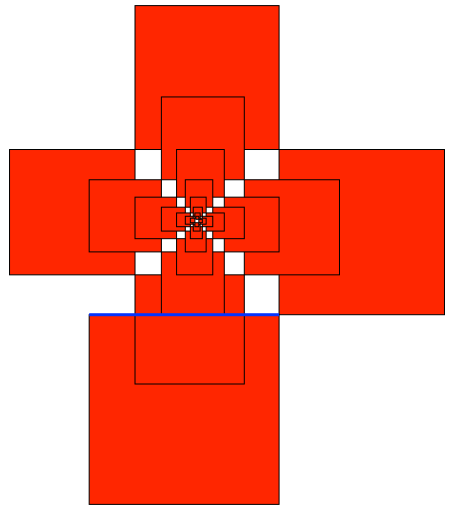
Abb. 12. Zwei Runden

Abb. 13: Zwei Runden

Der zugehörige Streckfaktor f ist die reelle Lösung der Gleichung:

Der numerische Wert ist f ≈ 0.8709940283.

6.2 Drei Runden

Wir arbeiten mit der reellen Lösung der Gleichung:

Der numerische Wert ist f ≈ 0.9123013893 (Abb. 14 und 15).

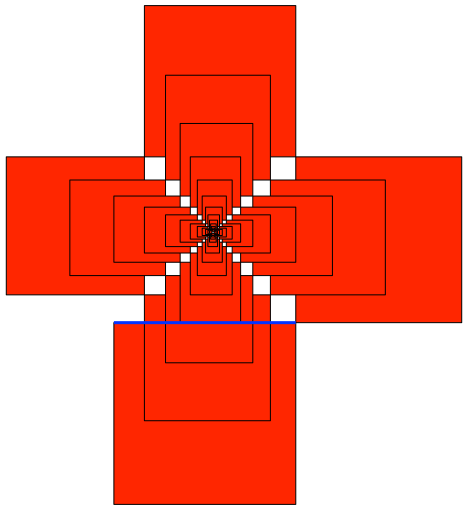
Abb. 14: Drei Runden

Abb. 15: Drei Runden

Literatur

Walser, Hans (2022): Spiralen, Schraubenlinien und spiralartige Figuren. Mathematische Spielereien in zwei und drei Dimensionen. Springer Spektrum. ISBN 978-3-662-65131-5 und ISBN 978-3-662-65132-2 (eBook).