Hans Walser, [20160501]

Quadrate ansetzen

1 Worum geht es?

Einem regelmäßigen n-Eck setzen wir Quadrate an und iterieren den Prozess. Die Quadratflächen bilden eine Folge, die mit der Fibonacci-Folge verwandt ist.

Mitteilung von Resultaten.

2 Zweieck als Basis

Wir setzen einer Strecke zunächst zwei rote Quadrate an, anschließend zwei grüne und dann zwei blaue (Abb.1).

Abb. 1: Start mit einer Strecke

Weiter setzen wir zwei zyan, zwei magenta und zwei goldgelbe Quadrate an (Abb. 2).

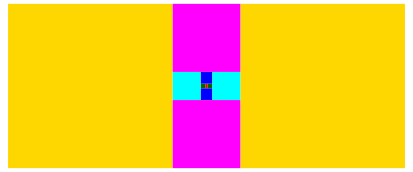
Abb. 2: Weitere Quadratpaare

Die Startstrecke habe die Länge 1.

Mit f₁ bezeichnen wir den Flächeninhalt eines roten Quadrates, mit f₂, f₃, f₄, ... den Flächeninhalt eines grünen, blauen, zyan, ... Quadrates.

Wir erhalten (Tab. 1):

n	1	2	3	4	5	6
fn	1	4	25	144	841	4900
fn = an^2	1^2	2^2	5^2	12^2	29^2	70^2

Tab. 1: Quadratflächen

Es sind alles Quadratzahlen.

Es gilt die Rekursion:

(1)

Für den Koeffizienten 5 in (1) gilt:

(2)

Für die Quadratwurzeln gilt die Rekursion:

(3)

Die Tabelle 2 gibt weitere Werte.

n	fn	fn+1/fn	an	an+1/an
1	1	4	1	2
2	4	6.250000000	2	2.500000000
3	25	5.760000000	5	2.400000000
4	144	5.840277778	12	2.416666667
5	841	5.826397146	29	2.413793103
6	4900	5.828775510	70	2.414285714
7	28561	5.828367354	169	2.414201183
8	166464	5.828437380	408	2.414215686
9	970225	5.828425365	985	2.414213198
10	5654884	5.828427427	2378	2.414213625
11	32959081	5.828427073	5741	2.414213552
12	192099600	5.828427134	13860	2.414213564
13	1119638521	5.828427123	33461	2.414213562
14	6525731524	5.828427125	80782	2.414213562
15	38034750625	5.828427125	195025	2.414213562
16	221682772224	5.828427125	470832	2.414213562
17	1292061882721	5.828427125	1136689	2.414213562
18	7530688524100	5.828427125	2744210	2.414213562
19	43892069261881	5.828427125	6625109	2.414213562
20	255821727047184	5.828427125	15994428	2.414213562

Tab. 2: Weitere Werte

Es gelten folgende Grenzwerte:

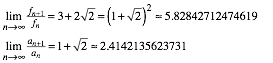(4)

Aus dem zweiten Grenzwert folgt, dass sich die Umrissrechtecke der Abbildungen 1 und 2 einem Rechteck mit dem Seitenverhältnis annähern. Dieses Grenzrechtreck wird als Silbernes Rechteck bezeichnet (Walser 2013a, S. 116), (Walser 2013b, S. 63f).

3 Dreieck als Basis

Wir starten mit einem gleichseitigen Dreieck der Seitenlänge 1 (Abb. 3 und 4).

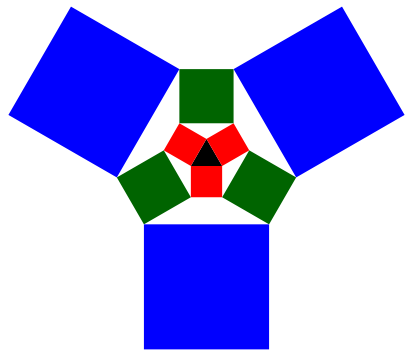
Abb. 3: Start mit einem gleichseitigen Dreieck

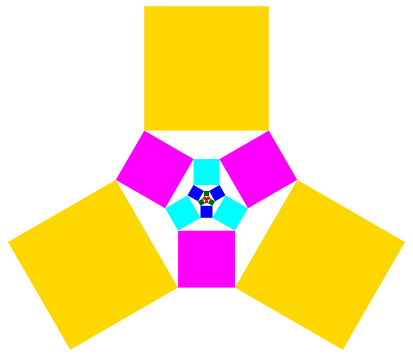
Abb. 4: Weitere Quadrate

Wir erhalten entsprechend (Tab. 3):

n	1	2	3	4	5	6
fn	1	3	16	75	361	1728
Bemerkungen	1^2		4^2		19^2	12^3

Tab. 3: Quadratflächen

Es gilt die Rekursion:

(5)

Für den Koeffizienten 4 in (5) gilt:

(6)

Tabelle 4 gibt weitere Werte.

n	fn	fn+1/fn	Bemerkungen
1	1	3	1^2
2	3	5.333333333
3	16	4.687500000	4^2
4	75	4.813333333
5	361	4.786703601	19^2
6	1728	4.792245370	12^3
7	8281	4.791088033	91^2
8	39675	4.791329553
9	190096	4.791279143	436^2
10	910803	4.791289664
11	4363921	4.791287468	2089^2
12	20908800	4.791287927
13	100180081	4.791287831	10009^2
14	479991603	4.791287851
15	2299777936	4.791287847	47956^2
16	11018898075	4.791287848
17	52794712441	4.791287847	229771^2
18	252954664128	4.791287847
19	1211978608201	4.791287847	1100899^2
20	5806938376875	4.791287847

Tab. 4: Weitere Werte

Jede zweite Zahl ist eine Quadratzahl. Die Kubikzahl 1728 = 12³ ist singulär.

Wir haben den Grenzwert:

(7)

Die Folge b_n der ganzzahligen Wurzeln

1,4,19, 91, 436, ... (8)

hat die Rekursion

(9)

Die Quotienten-Folge der Folge b_n hat ebenfalls den Grenzwert (7).

Und nun das Überraschende: Wir können auch mit einem beliebigen Dreieck starten (Abb. 5 und 6).

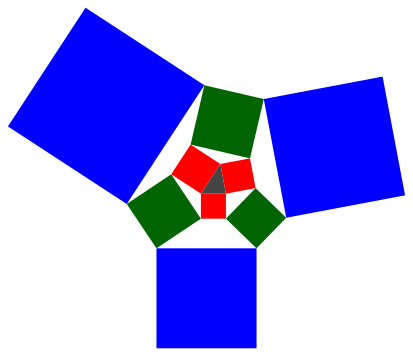
Abb. 5: Start mit einem beliebigen Dreieck

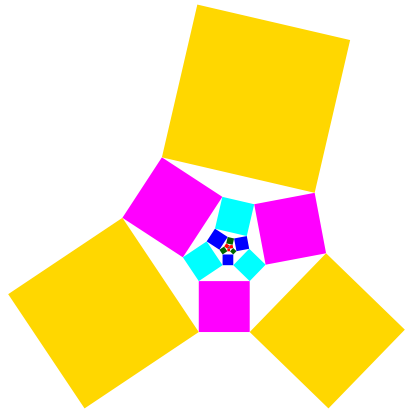
Abb. 6: Weitere Quadrate

Die Quadrate derselben Farbe sind nicht mehr gleich groß. Daher ersetzen wir die einzelnen Quadratflächen durch die Summen der Quadratflächen gleicher Farbe. So sei s₁ die Flächensumme der drei roten Quadrate, s₂, s₃, s₄, ... die Flächensummen der grünen, blauen, zyan, ... Quadrate.

Die Maßzahlen sind jetzt nicht mehr „schön“, aber es gilt für die Folge s_n nach wie vor die Rekursion entsprechend zu (5):

(10)

Ich habe keinen Beweis für diesen Sachverhalt.

4 Quadrat als Basis

Wir starten mit einem Quadrat der Seitenlänge 1. Die Abbildung 7 zeigt die Situation.

Abb. 7: Start mit einem Quadrat

Wir erhalten entsprechend (Tab. 5):

n	1	2	3	4	5	6
fn	1	2	9	32	121	450
Bemerkungen	1^2		3^2		11^2

Tab. 5: Quadratflächen

Es gilt die Rekursion:

(11)

Für den Koeffizienten 3 in (11) gilt:

(12)

Tabelle 6 gibt weitere Werte.

n	fn	fn+1/fn	Bemerkungen
1	1	2	1^2
2	2	4.500000000
3	9	3.555555556	3^2
4	32	3.781250000
5	121	3.719008264	11^2
6	450	3.735555556
7	1681	3.731112433	41^2
8	6272	3.732302296
9	23409	3.731983425	153^2
10	87362	3.732068863
11	326041	3.732045970	571^2
12	1216800	3.732052104
13	4541161	3.732050460	2131^2
14	16947842	3.732050901
15	63250209	3.732050783	7953^2
16	236052992	3.732050814
17	880961761	3.732050806	29681^2
18	3287794050	3.732050808
19	12270214441	3.732050807	110771^2
20	45793063712	3.732050808

Tab. 6: Weitere Werte

Jede zweite Zahl ist eine Quadratzahl.

Wir haben für die Quotienten-Folge den Grenzwert:

(13)

Die Folge b_n der ganzzahligen Wurzeln

1, 3, 11, 41, 153, ... (14)

hat die Rekursion

(15)

Die Quotienten-Folge der Folge b_n hat ebenfalls den Grenzwert (13).

Leider ist es so, dass entsprechendes für ein beliebiges Viereck als Startfigur nicht gilt.

5 Fünfeck als Basis

Wir starten mit einem regelmäßigen Fünfeck der Seitenlänge 1. Die Abbildung 8 zeigt die Situation.

Abb. 8: Start mit einem regelmäßigen Fünfeck

Für die Quadratflächen erhalten wir (Tab. 7):

n	1	2	3	4	5	6
fn	1
fn	1
fn	1	1.381966	5.673762	15.806504	49.783299	150.558920

Tab. 7: Quadratflächen

Die Zahlen sind unschön, erinnern aber an den Goldenen Schnitt.

Es gilt die Rekursion:

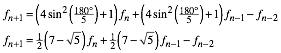(16)

Tabelle 8 gibt weitere Werte.

n	fn	fn+1/fn
1	1	1.381966012
2	1.381966012	4.105572810
3	5.673762082	2.785894840
4	15.80650451	3.149545107
5	49.78329894	3.024285726
6	150.5589204	3.064593260
7	461.4018527	3.051323818
8	1407.886463	3.055659975
9	4302.022314	3.054239569
10	13139.40678	3.054704486

Tab. 8: Weitere Werte

Wir haben für die Quotienten-Folge den Grenzwert:

(17)

6 Sechseck als Basis

Wir starten mit einem regelmäßigen Sechseck der Seitenlänge 1. Die Abbildung 9 zeigt die Situation. Vgl. (Walser, 2012, S. 28-30).

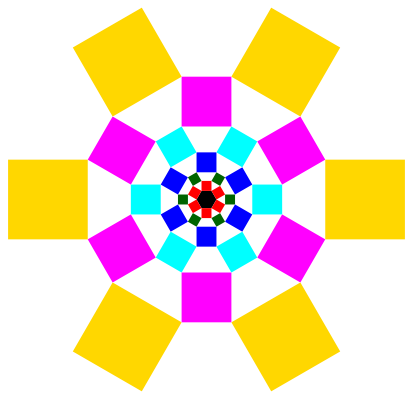
Abb. 9: Start mit einem regelmäßigen Sechseck

Wir erhalten (Tab. 9):

n	1	2	3	4	5	6
fn	1	1	4	9	25	64
Bemerkungen	1^2	1^2	2^2	3^2	5^2	8^2

Tab. 9: Quadratflächen

Wir erhalten die Quadrate der Fibonacci-Zahlen.

Es gilt die Rekursion:

(18)

Für den Koeffizienten 2 in (18) gilt:

(19)

Die Tabelle 10 gibt weitere Werte.

n	fn	fn+1/fn
1	1	1
2	1	4
3	4	2.250000000
4	9	2.777777778
5	25	2.560000000
6	64	2.640625000
7	169	2.609467456
8	441	2.621315193
9	1156	2.616782007
10	3025	2.618512397
11	7921	2.617851281
12	20736	2.618103781
13	54289	2.618007331
14	142129	2.618044171
15	372100	2.618030099
16	974169	2.618035474
17	2550409	2.618033421
18	6677056	2.618034205
19	17480761	2.618033906
20	45765225	2.618034020

Tab. 10: Weitere Werte

Wir haben für die Quotienten-Folge den Grenzwert:

(20)

Der Grenzwert ist das Quadrat des Goldenen Schnittes.

7 Siebeneck als Basis

Wir starten mit einem regelmäßigen Siebeneck der Seitenlänge 1 (Abb. 10).

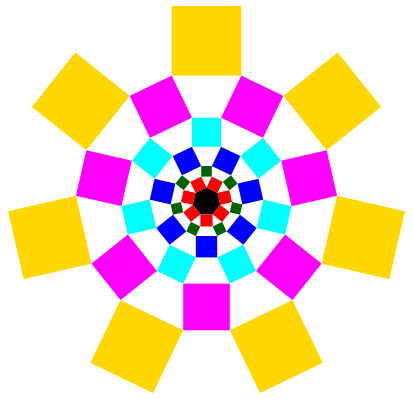
Abb. 10: Start mit einem regelmäßigen Siebeneck

Wir erhalten (Tab. 11):

n	1	2	3	4	5	6
fn	1
fn	1	0.75302	3.07308	5.70723	14.63905	32.59437

Tab. 11: Quadratflächen

Es gilt die Rekursion:

(21)

Die Tabelle 12 gibt weitere Werte.

n	fn	fn+1/fn
1	1	0.7530203968
2	0.7530203968	4.081005675
3	3.073080512	1.857170000
4	5.707232935	2.564999245
5	14.63904817	2.226535830
6	32.59436527	2.365252509
7	77.09390424	2.304290169
8	177.6467256	2.330305573
9	413.9711547	2.319060871
10	960.0243067	2.323894644

Tab.12: Weitere Werte

Wir haben für die Quotientenfolge den Grenzwert:

(22)

8 Zusammenfassung

Für ein regelmäßiges k-Eck als Startfigur ergibt sich die Rekursion:

(23)

Für den Grenzwert der Quotienten-Folge erhalten wir:

(24)

Die Tabelle 13 gibt die Grenzwerte.

Eckenzahl k
2	5.828427124
3	4.791287848
4	3.732050808
5	3.054589814
6	2.618033988
7	2.322438488
8	2.112388720
9	1.956898374
10	1.837852792
11	1.744146651
12	1.668669260
13	1.606690570
14	1.554958131
15	1.511170296
16	1.473656957
17	1.441179400
18	1.412800982
19	1.387801235
20	1.365617499

Tab. 13: Grenzwerte der Quotienten-Folgen

Literatur

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.

Walser, Hans (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Edition am Gutenbergplatz, Leipzig. ISBN 978-3-937219-85-1.

Walser, Hans (2013b): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.