Hans Walser, [20190313a]

Quadrat und Quadrate

1 Worum geht es?

Zu einem Quadrat finden wir vier weitere Quadrate, deren alternierende Flächensumme null ergibt.

2 Disposition

Wir zeichnen ein Quadrat und dazu ein beliebiger Punkt (Abb. 1). Dieser Punkt kann innerhalb oder außerhalb des Quadrates liegen. Er muss nicht auf die Symmetrien des Quadrates abgestimmt sein.

Abb. 1: Quadrat und Punkt

Nun passen wir ein erstes Quadrat so ein, dass eine Ecke auf dem beliebigen Punkt und die diametrale Ecke auf einem Eckpunkt des gezeichneten Quadrates liegen (Abb. 2).

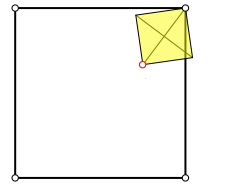
Abb. 2: Erstes Quadrat einpassen

Analog passen wir die drei restlichen Quadrate ein (Abb. 3).

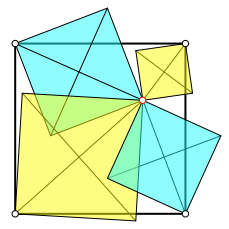
Abb. 3: Die restlichen drei Quadrate einpassen

Die Quadrate überschneiden sich teilweise.

Wir färben die Quadrate alternierend gelb und blau.

3 Ein Flächensatz

Die Summe der gelben Quadratflächen ist gleich groß wie die Summe der blauen Quadratflächen.

Dies kann auch so formuliert werden: die alternierende Flächensumme ist null.

4 Beweis

Für den Beweis führen wir ein Koordinatensystem ein gemäß Abbildung 4. Das Startquadrat hat darin die Seitenlänge 2.

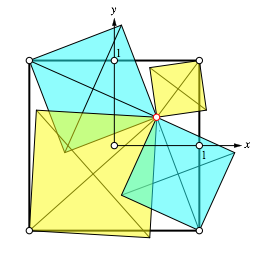
Abb. 4: Koordinatensystem

Der beliebig gewählte Punkt habe die Koordinaten .

Der Flächeninhalt eines eingepassten Quadrates ist gleich der Hälfte des Quadrates seiner Diagonalenlänge.

Das erste eingepasste Quadrat hat nach Pythagoras folgendes Quadrat der Diagonalenlänge:

(1)

(2) gibt die vollständige Liste:

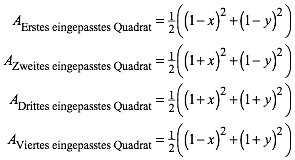(2)

Wir sehen, dass die alternierende Summe verschwindet. Dies war zu zeigen.

Bemerkung 1: Diese Studie entstand als Nebenresultat von [1].

Bemerkung 2: Wie steht es im Raum?

Weblink

[1] Hans Walser: Kreisscharen

http://www.walser-h-m.ch/hans/Miniaturen/K/Kreisscharen2/Kreisscharen2.htm