Hans Walser, [20200804]

Pythagoreische 60°- und 120°-Dreiecke

1 Worum geht es?

Wir fragen nach Dreiecken mit einem Winkel oder und ganzzahligen Seitenlängen.

Dies in Analogie zu den rechtwinkligen pythagoreischen Dreiecken.

2 Winkel 60°

Aus dem Kosinus-Satz ergibt sich:

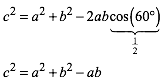(1)

2.1 Parametrisierungen

Ich habe zwei Parametrisierungen gefunden.

2.1.1 Erste Parametrisierung

Es sei u > v ≥ 0, u, v teilerfremd und u – v nicht durch 3 teilbar. Mit

(2)

ist (1) erfüllt. Nachweis durch Nachrechnen.

2.1.2 Zweite Parametrisierung

Es sei u > v ≥ 0, u, v teilerfremd und u – v nicht durch 3 teilbar. Mit

(3)

ist (1) ebenfalls erfüllt. Nachweis durch Nachrechnen.

Die beiden Parametrisierungen unterscheiden sich nur in a. Es ist . Während (3) eine Formelsymmetrie aufweist, ist (2) asymmetrisch. Dafür ist (2) näher an den ebenfalls asymmetrischen Formeln für rechtwinklige pythagoreische Dreiecke. Ich sehe da nicht durch.

Ich weiß nicht, ob man mit (2) und (3) alle pythagoreischen 60°-Dreiecke erhält.

2.2 Tabelle

Die Tabelle 1 gibt die ersten Beispiele.

u	v	a1	a2	b	c
1	0	1	0	1	1
2	1	3	5	8	7
3	1	8	7	15	13
3	2	5	16	21	19
4	3	7	33	40	37
5	1	24	11	35	31
5	3	16	39	55	49
5	4	9	56	65	61
6	1	35	13	48	43
6	5	11	85	96	91
7	2	45	32	77	67
7	3	40	51	91	79
7	5	24	95	119	109
7	6	13	120	133	127
8	1	63	17	80	73
8	3	55	57	112	97
8	7	15	161	176	169
9	1	80	19	99	91
9	2	77	40	117	103
9	4	65	88	153	133
9	5	56	115	171	151
9	7	32	175	207	193
9	8	17	208	225	217
10	3	91	69	160	139
10	9	19	261	280	271

Tab. 1: Pythagoreische 60°-Dreiecke

Die Abbildung 1 zeigt die beiden Lösungen a₁ = 3, b =8, c = 7 und a₂ =5, b =8, c = 7.

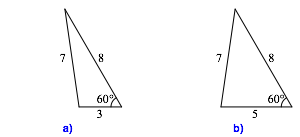
Abb. 1: Die beiden Lösungen

Wenn man die eine Lösung spiegelt, ergänzen sie sich zum gleichseitigen Dreieck (Abb. 2).

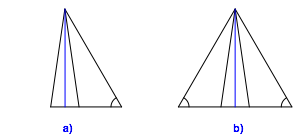
Abb. 2: Ergänzung zum gleichseitigen Dreieck

Die Abbildung 3 zeigt ein Lochstreifenmodell dazu. Es zählen die Zwischenräume zwischen den Löchern, nicht die Löcher (Zaunpfahlproblem).

Abb. 3: Lochstreifenmodell

3 Winkel 120°

3.1 Parametrisierung

Es sei u > v ≥ 0, u, v teilerfremd und u – v nicht durch 3 teilbar. Mit

(4)

ergeben sich solche Dreiecke.

Ich weiß nicht ob man mit (4) alle pythagoreischen 120°-Dreiecke erhält.

3.2 Tabelle

Die Tabelle 2 gibt die ersten Beispiele.

u	v	a	b	c
2	1	3	5	7
3	1	8	7	13
3	2	5	16	19
4	3	7	33	37
5	1	24	11	31
5	3	16	39	49
5	4	9	56	61
6	1	35	13	43
6	5	11	85	91
7	2	45	32	67
7	3	40	51	79
7	5	24	95	109
7	6	13	120	127
8	1	63	17	73
8	3	55	57	97
8	7	15	161	169
9	1	80	19	91
9	2	77	40	103
9	4	65	88	133
9	5	56	115	151
9	7	32	175	193
9	8	17	208	217
10	3	91	69	139
10	9	19	261	271

Tab. 2: Pythagoreische 120°-Dreiecke

In den beiden Tabellen 1und 2 sind (bis auf das gleichseitige Dreieck zuoberst) die beiden Spalten für c identisch. Die a- und die b-Spalte der Tabelle 2 entsprechen den a₁- und a₂-Spalten der Tabelle 1.

Der Hintergrund liegt darin, dass man aus einem 60°-Dreieck durch Abschneiden eines gleichseitigen Dreiecks ein 120°-Dreieck erhält (Abb. 4).

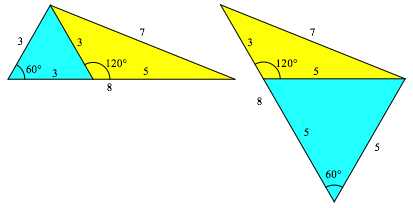
Abb. 4: Abschneiden eines gleichseitigen Dreiecks

Die Abbildungen 5 und 6 zeigen die Überlagerung der beiden Möglichkeiten.

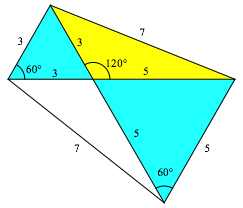
Abb. 5: Überlagerung

Abb. 6: Lochstreifenmodell