Hans Walser, [20080316a]

Polygone im Raum

Anregung: Chr. W., B.

1 Worum es geht

Wir untersuchen die Winkelsumme von geschlossenen räumlichen Polygonen. Diese Winkelsumme ist kleiner oder gleich der Winkelsumme des ebenen Polygons gleicher Eckenzahl, mit Gleichheit genau im Fall eines ebenen Polygons. Die Überlegungen benützen die Richtungsänderungen der Seitenvektoren, also die Außenwinkel.

2 Beispiele

In einem ebenen Fünfeck ist die Winkelsumme . Die linke Figur zeigt ein nicht ebenes räumliches Fünfeck mit fünf rechten Winkeln, also der Winkelsumme 450°. Im Fünfeck der rechten Figur sind zwei rechte Winkel, zwei Winkel von 45° und ein Winkel von 60°, zusammen 330°.

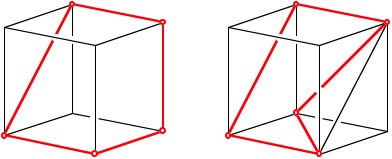
Räumliche Fünfecke

3 Das sphärische Außenwinkelbild

Wir zeichnen zu einem ebenen Polygon die Richtungsänderungen der Seitenvektoren als Außenwinkelsektoren ein. Durch Zusammensetzen dieser Außenwinkelsektoren erhalten wir eine Kreisscheibe. Die Summe der Außenwinkel ist 2π.

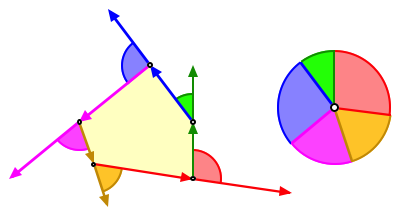
Zusammensetzung der Außenwinkel

Wird der Radius der Winkelsektoren gleich 1 gewählt, sind die Winkelbogen die Außenwinkel im Bogenmaß und die Kreisscheibe der Einheitskreis.

Da sich Innen- und Außenwinkel je auf π ergänzen, ergibt sich für ein ebenes Polygon mit n Ecken die Innenwinkelsumme .

Für ein räumliches Polygon führt das entsprechende Vorgehen auf eine Figur in der Einheitskugel, das sphärische Außenwinkelbild. Dieses sphärische Außenwinkelbild hat folgende Eigenschaften:

Auf der Oberfläche der Einheitskugel ergibt sich ein Polygon, das aus Großkreisbogen zusammengesetzt ist. Die Längen dieser Großkreisbogen entsprechen den Außenwinkeln. Die Richtung vom Kugelmittelpunkt zu einem Eckpunkt dieses Großkreisbogen-Polygons ist gleich der Richtung des entsprechenden Seitenvektors des räumlichen Polygons.

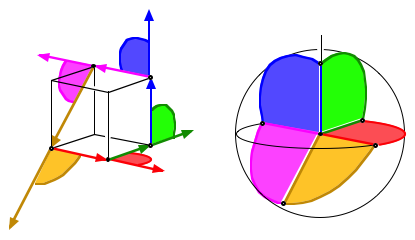
Sphärisches Außenwinkelbild

4 Die Außenwinkelsumme

Es gilt:

In einem geschlossenen räumlichen Polygon ist die Außenwinkelsumme größer oder gleich , mit Gleichheit genau beim ebenen Polygon.

Der Beweis geht indirekt mit einer Fallunterscheidung.

Fall 1: Die Gesamtlänge des sphärischen Außenwinkelbildes sei kleiner als .

Eine geschlossene Kurve auf der Oberfläche der Einheitskugel, deren Gesamtlänge kleiner als ist, verläuft vollständig in einer Halbsphäre. Durch Drehen der Situation können wir erreichen, dass dies die obere (nördliche) Halbsphäre ist.

Dies gilt insbesondere auch für das sphärische Außenwinkelbild. Nun sind die Richtungen vom Kugelmittelpunkt zu den Ecken des sphärischen Außenwinkelbildes die Richtungen der Seitenvektoren des ursprünglichen räumlichen Polygons. Diese Richtungen weisen alle nach oben, das räumliche Polygon schraubt sich also in die Höhe und kann nicht geschlossen sein.

Fall 2: Die Gesamtlänge des sphärischen Außenwinkelbildes sei gleich .

Sonderfall 2.1: Das sphärische Außenwinkelbild ist ein Großkreis. Dann liegen alle Seitenvektoren des räumlichen Polygons in einer Ebene, das Polygon ist eben.

Sonderfall 2.2: Das sphärische Außenwinkelbild besteht aus zwei halben Großkreisen (Figur).

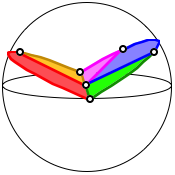
Zwei halbe Kreisscheiben

In diesem Sonderfall sind zwei Seitenvektoren horizontal, alle übrigen weisen nach oben. Das räumliche Polygon ist nicht geschlossen.

In den übrigen Fällen liegt das sphärische Außenwinkelbild auf einer Halbsphäre; das Polygon ist nicht geschlossen.

Die Außenwinkelsumme ist somit , mit Gleichheit genau beim ebenen Polygon. Die Innenwinkelsumme eines Polygons mit n Ecken ist daher kleiner , mit Gleichheit genau beim ebenen Polygon.

5 Spezielle räumliche Polygone

5.1 Gleichseitiges Polygon

In einem gleichseitigen räumlichen Polygon sind alle Seitenvektoren gleich lang und können auf die Länge 1 normiert werden. Im sphärischen Außenwinkelbild sind sie dann direkt die Vektoren vom Kugelzentrum zu den Ecken des sphärischen Außenwinkelbildes. In einem geschlossenen gleichseitigen Polygon ist die Summe der Seitenvektoren null; der Schwerpunkt der Ecken des sphärischen Außenwinkelbildes ist also der Kugelmittelpunkt.

5.2 Gleichwinkliges Polygon

Die Innenwinkel und damit auch die Außenwinkel sind gleich. Das sphärisches Außenwinkelbild ist ein gleichseitiges Großkreisbogen-Polygon.

In einem gleichwinkligen Polygon mit n Ecken ist der Außenwinkel , der Innenwinkel , mit Gleichheit genau beim ebenen gleichwinkligen Polygon.

5.3 Gleichseitig-gleichwinkliges Polygon

Das zugehörige Außenwinkelbild ist ein gleichseitiges Großkreisbogen-Polygon mit dem Eckenschwerpunkt im Kugelmittelpunkt.

5.3.1 Gleichseitig-gleichwinkliges Fünfeck

Nach einem Satz von B. L. van der Waerden ist ein gleichseitig-gleichwinkliges Fünfeck eben, also das reguläre ebene Pentagon (vgl. [van der Waerden 1970], [Lüssy/Trost 1970], [Irminger 1970]).

5.3.2 Gleichseitig-gleichwinkliges Polygon gerader Eckenzahl

Das einfachste Beispiel eines nicht ebenen gleichseitig-gleichwinkligen Polygons gerader Eckenzahl sind die Mantelkanten eines geraden Antiprismas mit einem regulären n-Eck als Deck- und Grundfläche. Deck- und Grundfläche können in der Höhe beliebig auseinander gezogen werden. Dadurch wird der Innenwinkel beliebig klein. Das Polygon hat eine n-teilige Drehsymmetrie. Die Figur zeigt ein Beispiel für .

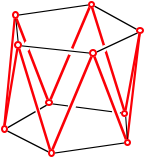
Gleichseitig-gleichwinkliges Zehneck

5.3.3 Gleichseitig-gleichwinkliges Polygon mit nicht primer Eckenzahl

Die Eckenzahl sei mn.

Wir denken uns eine Girlande aus mn gleich langen Strecken, welche in n Abschnitte zu je m Strecken unterteilt ist. Die Strecken sollen and den Enden gelenkig verbunden sein. Die Figur zeigt die ebene Situation für und , also für .

Girlande

Diese Girlande denken wir uns nun als sphärisches Außenwinkelbild auf der Einheitskugel. Statt Strecken nehmen wir jetzt gleich lange Großkreisbogen. Die Gesamtlänge soll etwas größer als 2π sein. Die n Aufhängepunkte denken wir uns gleichmäßig auf einem nördlichen Breitenkreis verteilt; der erste und der letzte Aufhängepunkt sind zu identifizieren. Der Schwerpunkt der mn Girlanden-Ecken liegt aus Symmetriegründen auf der Kugelachse.

Nun bewegen wir den Aufhänge-Breitenkreis nach oben oder unten, bis der Schwerpunkt der Girlanden-Ecken auf den Kugelmittelpunkt zu liegen kommt. Dann können wir die Vektoren vom Kugelmittelpunkt zu den Girlanden-Ecken der Reihe nach zu einem räumlichen Polygon zusammensetzen. Dieses ist geschlossen, gleichseitig und gleichwinklig, aber nicht eben. Es hat eine n-teilige Drehsymmetrie.

5.3.4 Offene Frage

Die Frage ist offen, ob es für eine Primzahl größer als 5 ein nicht ebenes gleichseitig-gleichwinkliges Polygon gibt. Die Überlegungen von van der Waerden lassen sich nicht auf beliebige Primzahlen übertragen. Der Grund liegt darin, dass es im gleichseitig-gleichwinkligen Fünfeck nur einen Typ von Diagonalen gibt, alle diese Diagonalen sind gleich lang.

Literatur

[Irminger 1970] Irminger, H.: Zu einem Satz über räumliche Fünfecke. Elemente der Mathematik. Band 25, 1970, S. 135-136

[Lüssy/Trost 1970] Lüssy, W. und E. Trost: Zu einem Satz über räumliche Fünfecke. Elemente der Mathematik. Band 25, Heft 4, 10. Juli 1970, S. 82-83

[van der Waerden 1970] Van der Waerden, B. L.: Ein Satz über räumliche Fünfecke. Elemente der Mathematik. Band 25, Heft 4, 10. Juli 1970, S. 73-78