Hans Walser, [20140111]
Regular
polygon in the square
We inscribe a regular polygon in the square such that one side of the polygon is parallel to a diagonal of the square. Figure 1 depicts the situation for n = 11.
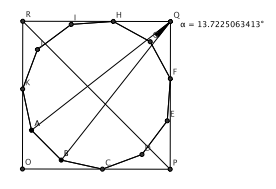
Fig. 1: Eleven-gon in the square
The
angle 
is
close to 150ˇ/11 = 13.6364ˇ.
One
may think that for 
we get the limit:
ThatŐs not right. To see this, we consider the special case of regular n-gons where n is a multiple of 8 (Fig. 2 for n = 24).
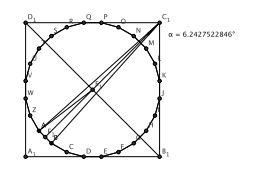
Fig. 2: 24-gon in the square
In
this special case itŐs easy to inscribe the polygon in the square. For the
angle 
we have in this special case:
Table 1 gives some examples.
|
n |
|
|
|
8 |
19.47122064ˇ |
155.7697651ˇ |
|
16 |
9.420172938ˇ |
150.7227670ˇ |
|
24 |
6.242752283ˇ |
149.8260548ˇ |
|
32 |
4.672340688ˇ |
149.5149020ˇ |
|
40 |
3.734283802ˇ |
149.3713521ˇ |
|
48 |
3.110281217ˇ |
149.2934984ˇ |
|
56 |
2.665117811ˇ |
149.2465974ˇ |
|
64 |
2.331502714ˇ |
149.2161737ˇ |
|
72 |
2.072157264ˇ |
149.1953230ˇ |
|
80 |
1.864755156ˇ |
149.1804125ˇ |
|
88 |
1.695106618ˇ |
149.1693824ˇ |
|
96 |
1.553760358ˇ |
149.1609944ˇ |
|
104 |
1.434177567ˇ |
149.1544670ˇ |
|
112 |
1.331690076ˇ |
149.1492885ˇ |
|
120 |
1.242875923ˇ |
149.1451108ˇ |
|
128 |
1.165169469ˇ |
149.1416920ˇ |
|
136 |
1.096609254ˇ |
149.1388586ˇ |
|
144 |
1.035670029ˇ |
149.1364842ˇ |
|
152 |
0.9811478612ˇ |
149.1344749ˇ |
|
160 |
0.9320797475ˇ |
149.1327596ˇ |
|
1000 |
0.1491172888ˇ |
149.1172888ˇ |
|
1000000 |
0.0001491168825ˇ |
149.1168825ˇ |
Tab. 1: Examples
We
see, that the limit of 
seems not
to be 150ˇ.
In fact, the limit is in our case:
We can prove this using the rule of Bernoulli – de lŐH™pital:
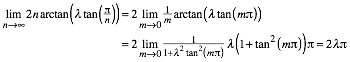
In our
case we have 
.