Hans Walser, [20150808]

Polardarstellung eines regelmŠ§igen Vielecks

1     Problemstellung

Ein regelmŠ§iges n-Eck soll in Polarkoordinaten dargestellt werden, also: . Dabei ist t der Polarwinkel,  der Polarabstand.

Gesucht ist die Funktion  in AbhŠngigkeit der Eckenzahl n.

2     Lšsung

Die Funktion

 

lšst das Problem. FŸr n = 7 ergibt sich die Figur der Abbildung 1. Es ist zusŠtzlich in Rot der Einheitskreis eingezeichnet. Das Siebeneck ist tangential an den Einheitskreis.

 

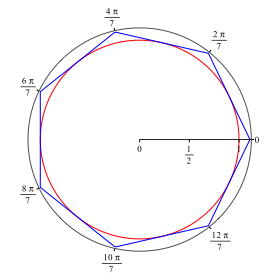
Abb.1: Siebeneck

 

Der schwarze Šu§ere Kreis ist die zu den Polarwinkeln gehšrende runde Achse des Koordinatensystems.

FŸr  ergibt sich die Figur der Abbildung 2. Es klappt also auch bei mehreren UmlŠufen.

 

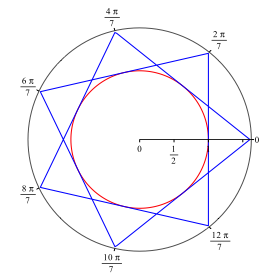
Abb. 2: Zwei UmlŠufe

 

3     Analyse der Lšsung

Wir analysieren Schritt fŸr Schritt (von innen nach au§en) die Lšsungsfunktion

 

fŸr . Die Abbildungen sind fŸr den Fall n = 7.

Die Abbildung 3.1 zeigt .

 

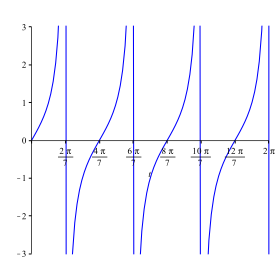
Abb. 3:1: Die PeriodizitŠt stimmt

 

Die Abbildung 3.2 zeigt .

 

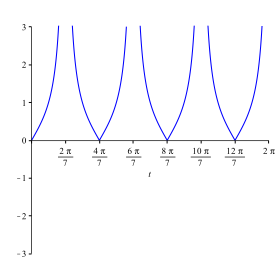
Abb. 3.2: AufwŠrts und abwŠrts

 

Die Abbildung 3.3 zeigt . Dies ist der wesentliche Schritt, weil wir so eine periodische Zickzacklinie erhalten.

 

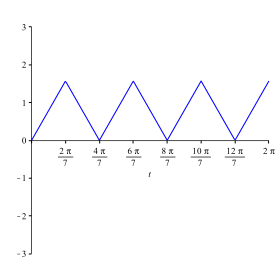
Abb. 3.3: Zickzacklinie

 

Die Abbildung 3.4 zeigt .

 

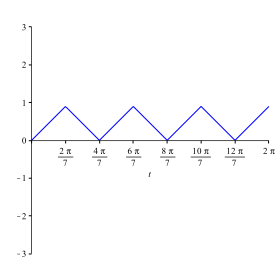
Abb. 3.4: Steigung eins und minus eins

 

Die Abbildung 3.5 zeigt .

 

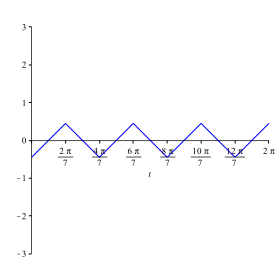
Abb. 3.5: Hšhenjustierung

 

Die Abbildung 3.6 zeigt . Die Spitzen weisen nach unten, in der Polardarstellung also nach innen.

 

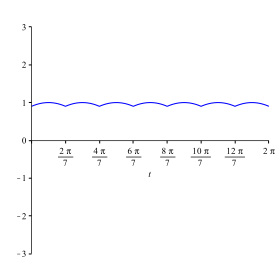
Abb. 3.6: Kosinusbšgen

 

Die Abbildung 3.7 zeigt . Die Spitzen weisen nach oben, in der Polardarstellung also nach au§en.

 

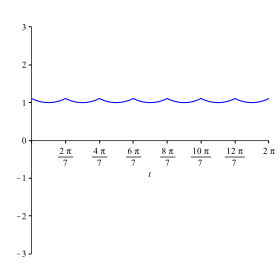
Abb. 3.7: Und nun die Funktion

 

4     Rosetten

Wenn wir den letzten Schritt nach Abbildung 3.7 weglassen, also mit der Funktion der Abbildung 3.6 arbeiten, ergeben sich Spitzen nach innen. Wir erhalten eine Rosette oder einen n-Pass (Abb. 4).

 

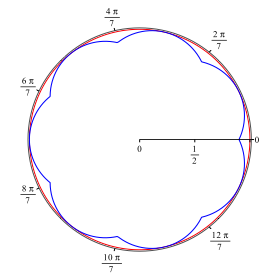
Abb. 4: Rosette

 

Wir kšnnen auch hier mit mehreren UmlŠufen arbeiten. Im Beispiel der Abbildung 5 sind drei UmlŠufe eingebarbeitet, . In dieser und den folgenden Abbildungen ist die Orientierung so geŠndert, dass die Figuren eine senkrechte Symmetrieachse erhalten. Zudem wird das Koordinatensystem weggelassen.

 

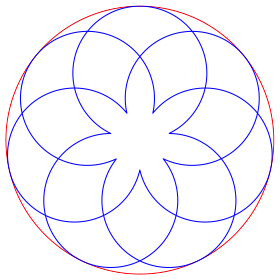
Abb.5: Drei UmlŠufe

 

Geometrisch entsteht die Rosette durch Einspiegelns des Sterns  am Einheitskreis (Abb. 6). Jeder Sternspitze nach au§en entspricht eine Rosettenspitze nach innen.

Da die Kreisspiegelung winkeltreu (konform) ist, schlie§en die Sternspitzen nach au§en und die Rosettenspitzen nach innen gleiche Winkel ein.

Da die Kreisspiegelung mšbiuskreistreu ist, sind die Rosettenbšgen echte Kreisbšgen.

 

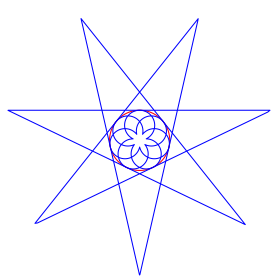
Abb. 6: Kreisspiegelung

 

Die Abbildung 7 zeigt einen Dreipass, wie er etwa in der gotischen Architektur erscheint.

 

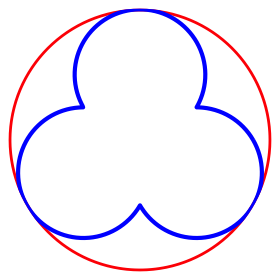
Abb. 7: Dreipass

 

5     Potenzierte regelmŠ§ige Vielecke

Wir ersetzen die Funktion  durch .

Die Abbildung 8 zeigt das Siebeneck fŸr p = 2, die Abbildung 9 fŸr p = 10. Die Seiten sind zunehmend nach au§en gebogen.

 

 

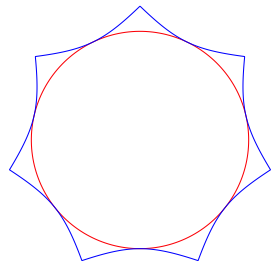
Abb. 8: Zweite Potenz. ãQuadratÒ

 

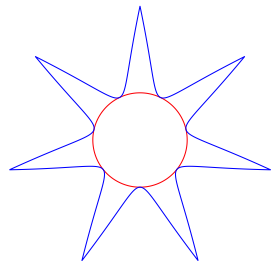
Abb. 9: Zehnte Potenz

 

Die Abbildungen 10 und 11 zeigen die Situation fŸr p = –2 und p = –10. Die rosettenbšgen sind keine Kreisbšgen mehr, sondern die Kreisspiegelbilder der in den Abbildungen 8 und 9 nach au§en gebogenen Seiten.

 

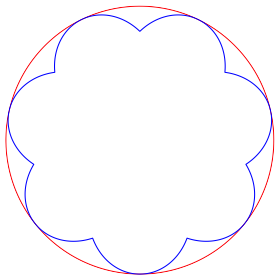
Abb. 10: Minus zweite Potenz

 

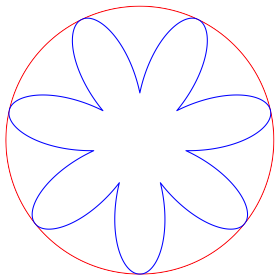
Abb. 11: Minus zehnte Potenz

 

Die Abbildungen 12 und 13 zeigen die Situation fŸr p = –30 und p = –100.

 

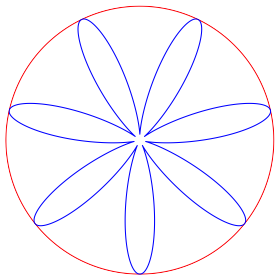
Abb. 12: p = –30

 

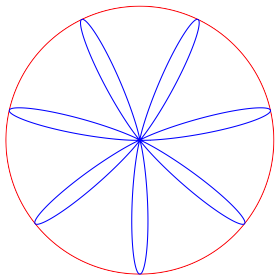
Abb. 13: p = –100

 

Die gewšhnlichen Rosetten gehšren zur minus ersten Potenz. Die nullte Potenz ergibt den Einheitskreis.

6     Spiralen

Wir ersetzen die Funktion  durch . FŸr a = 0.3 und  ergibt sich die Figur der Abbildung 14. Die Spitzen liegen auf einer logarithmischen Spirale.

 

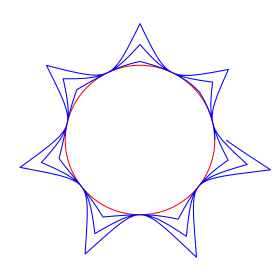
Abb. 14: Logarithmische Spirale

 

FŸr  setzt sich die Spirale nach innen ins Rosettenartige fort (Abb. 15).

 

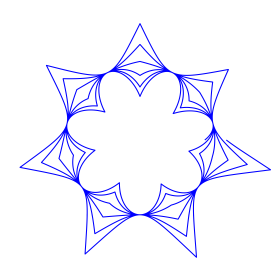
Abb. 15: Fortsetzung nach innen

 

7     Kugel

Wir arbeiten in sphŠrischen Koordinaten mit der Darstellung:

 

FŸr die folgenden Abbildungen wŠhlen wir n = 6.

FŸr p = 0 ergibt sich die Kugel (Abb. 16).

 

Abb. 16: Kugel

 

FŸr p = 1 ergibt sich eine Figur (Abb. 17), die in einem geeigneten Achsenschnitt (Abb. 18) und im €quatorschnitt (Abb. 19) je ein Sechseck aufweist. Die Figur ist aber kein Polyeder.

 

Abb. 17: p = 1

 

Abb. 18: Umriss ein Sechseck

 

Abb. 19: €quator ein Sechseck

 

FŸr p = 5 ergeben sich Spitzen nach au§en (Abb. 20). Der Stern hat aber nicht die Symmetrien eines platonischen Kšrpers.

 

Abb. 20: p = 5

 

FŸr p = –1 ergibt sich eine 3d-Rosette (Abb. 21).

 

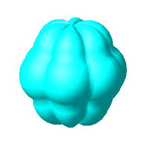
Abb. 21: p = –1

 

FŸr p = –5 ergibt sich was Knubliges (Abb. 22).

 

Abb. 22: p = –5