1 About

We discuss a theorem connecting an arbitrary right triangle to a parabola.

2 Situation

Let ABC be a right triangle with right angle at C (Fig. 1). M is the center of the circumcircle c and F the foot of the perpendicular from C to the hypotenuse AB. The line d is the tangent at the circumcircle c in the point C. Of course, the segment MC is orthogonal to the tangent c.

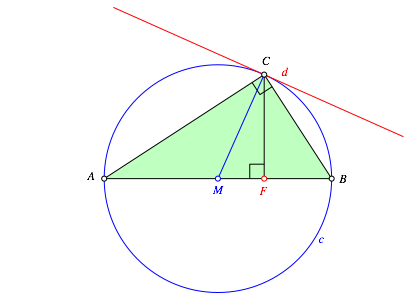
Fig. 1: Right triangle

3 The theorem

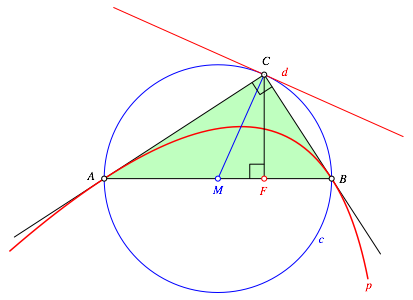
Fig. 2: Parabola

The parabola p with focus F and directrix d passes through the points A and B and is tangential to the legs CA and CB of the triangle ABC (Fig. 2).

4 Proof

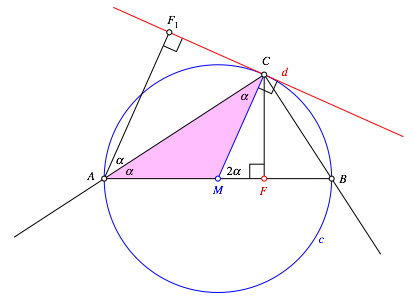
Fig. 3: Angles

The triangle CAM is isosceles. Therefore we have the angle . Now we draw the perpendicular from A to d. The perpendiculars AF₁ and MC are parallel. Hence and .

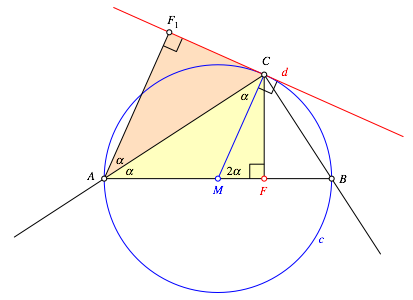
Fig. 4: Congruent triangles

Now the triangles CAF and CAF₁ are congruent (same angles, side CA in common) (Fig. 4). The triangle CAF₁ is just the mirror image of the triangle CAF.

Therefore the distance from A to F is equal to the distance from A to the line d. Hence A is a point of the parabola p. The line AC is angle bisector of the angle and therefore it is tangential to the parabola p.

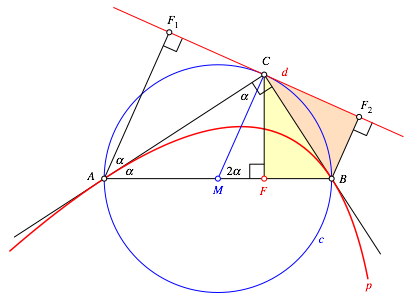
Fig. 5: Argumentation on the other side

An analogue argumentation holds for the point B (Fig. 5).

5 More tangents

5.1 Parallel to the hypotenuse

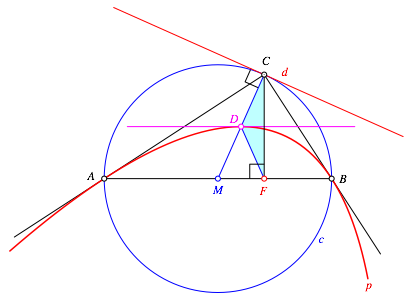
Fig. 6: Tangent parallel to the hypotenuse

The midpoint D of the segment MC is on the parabola p. The tangent in D at the parabola p is parallel to the hypotenuse AB. The proof is given by the isosceles triangle FCD.

5.2 Point of intersection

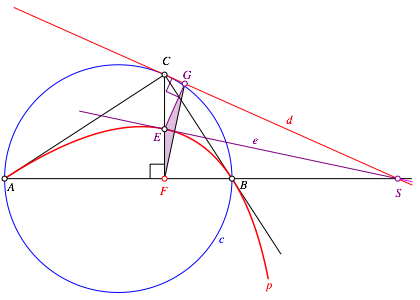
Fig. 7: Intersection of three lines

Let S be the point of intersection of the lines d and AB, and E the common point of the parabola p and the line FC. The tangent e at p through E passes also through S. The proof derives from the isosceles triangle FGE.