Hans Walser, [20180728]
Ortsbogen an Kegelschnitte
1 Worum geht es?
Gesucht sind die Punkte, von denen aus ein gegebener Kegelschnitt unter einem gegebenen Winkel gesehen wird. Bei Strecken wird diese Punktmenge als Ortsbogen bezeichnet, in Sonderfall eines rechten Winkels als Thaleskreis.
Bildliche Zusammenstellung von Resultaten.
2 Kurvenscharen
Der Kegelschnitt ist grźn gezeichnet.
Lila ist die Thaleskurve, die Menge der Punkte, von denen aus der Kegelschnitt unter einem rechten Winkel gesehen wird.
Rot sind die Ortsbšgen fźr andere Winkel. Der Winkelunterschied zwischen zwei benachbarten Kurven ist jeweils 15ˇ. Beispiel: Auf der zur Thaleskurve unmittelbar benachbarten Kurve in Richtung des Kegelschnittes liegen die Punkte, von denen aus der Kegelschnitt unter einem Winkel von 105ˇ gesehen wird.
3 Parabel
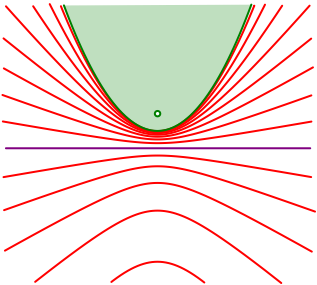
Abb. 1: Ortsbšgen an die Parabel
Die Thaleskurve ist die Leitgerade der Parabel.
Die źbrigen Ortsbšgen sind Hyperbeln, welche einen Brennpunkt im Brennpunkt der Parabel haben.
4 Ellipse
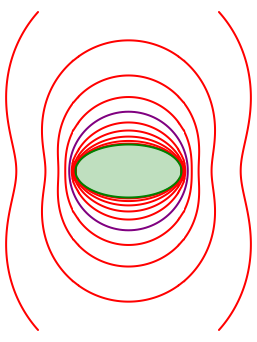
Abb. 2: Ortsbšgen an die Ellipse
Die
Thalesfigur ist ein Kreis mit dem Radius 
wobei a und b die Halbachsen der Ellipse bedeuten.
5 Hyperbel
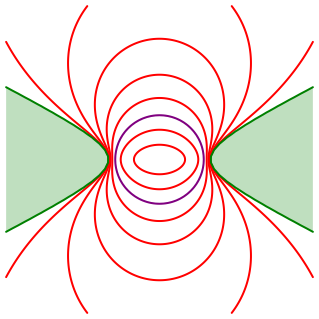
Abb. 3: Ortsbšgen an die Hyperbel
Die
Thalesfigur ist ein Kreis mit dem Radius 
wobei a und b die Halbachsen der Hyperbel bedeuten.
Der Sehwinkel kann nicht kleiner sein als derjenige Schnittwinkel der Asymptoten, in dessen Winkelfeld die Hyperbel liegt.
Weblinks
Hans Walser: Thaleskreis an Ellipse und Hyperbel (abgerufen 28. 07. 2018)
http://www.walser-h-m.ch/hans/Miniaturen/T/Thaleskreis_E_H/Thaleskreis_E_H.htm
Hans Walser: Sehwinkel bei Kegelschnitten (abgerufen 28. 07. 2018)
www.walser-h-m.ch/hans/Miniaturen/S/Sehwinkel_Kegelschnitte/Sehwinkel_Kegelschnitte.htm