Hans Walser, [20131206]

Orthoschem im Würfel

Anregung: A. L., S.

1 Das Orthoschem

Wir wählen im Würfel der Kantenlänge 1 drei aufeinanderfolgende paarweise orthogonale Kanten aus (Abb. 1a). Nun nehmen wir von diesen drei Kanten die konvexe Hülle (Abb. 1b).

Abb. 1: Orthoschem

So entsteht das Orthoschem, ein unregelmäßiges Tetraeder. Drei Kanten, nämlich die drei ausgewählten Würfelkanten, haben die Länge 1, zwei weitere Kanten ins Seitenflächendiagonalen der Länge und die längste Kante ist die Würfeldiagonale mit der Länge . Zwei der Seitenflächen sind rechtwinklig gleichschenklige Dreiecke (in der Abbildung 1c ist eines davon in Blau sichtbar), also längs einer Diagonalen halbierte Quadrate, die beiden anderen Seitenflächen sind rechtwinklige Dreiecke mit den Kathetenlängen 1 und (in der Abbildung 1c) ist eines davon in Cyan sichtbar), also längs einer Diagonalen halbierte Rechtecke im DIN-Format. Das Volumen des Orthoschems ist ein Sechstel des Würfelvolumens.

2 Chiralität

Das Orthoschem gibt es in zwei zueinander spiegelbildlichen Varianten (Abb. 2).

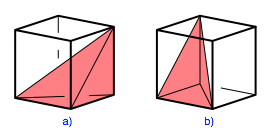
Abb. 2: Spiegelbildliche Varianten

Wir werden im Folgenden die Version der Abbildung 2a verwenden.

3 Einpassen in den Würfel

Das Orthoschem kann auf 12 verschiedene Arten in den Würfel eingepasst werden: Anlegen der langen Kante an eine der vier Würfeldiagonalen, dann Dritteldrehungen. Die Abbildung 3 zeigt die 12 Positionen.

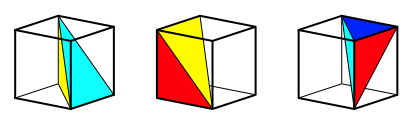
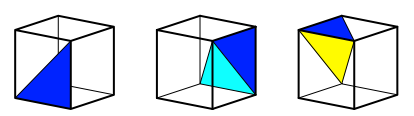
Abb. 3: Die 12 Positionen

Die drei Orthoscheme der obersten Reihe der Abbildung 3 können simultan und durchdringungsfrei in den Würfel gepackt werden (Abb. 4a). Sie haben eine Würfeldiagonale gemeinsam. Die Zwischenräume sind drei zu den bereits verbauten Orthoschemen spiegelbildliche Orthoscheme.

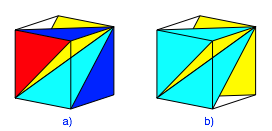
Abb. 4: Längs einer Würfeldiagonale

Die Abbildung 4b entsteht aus der Situation der Abbildung 4a durch Weglassen der rechtwinklig gleichschenkligen Dreiecke.

4 Ein Würfelmodell

Die Abbildung 4b gibt Anlass zu einem Würfelmodell wie folgt.

Wir falten eine DIN A6 Karte längs einer der beiden Diagonalen so dass die beiden Teile einen Schnittwinkel von 60° einschließen. Technisch geht das so: wir falten längs der Diagonalen, falten auf, drücken von der Rückseite (Bergfalt-Seite) her eine oder zwei Stapelklammern (Tacker-Klammern) quer über die Faltlinie in die Karte und biegen dann die Klammern zu einem Winkel von 60° zurecht. Die konvexe Hülle der gefalteten Karte ist ein Orthoschem.

Wir bauen nun sechs solche Orthoscheme, drei linke und drei rechte (Faltdiagonalen austauschen). Diese heften wir provisorisch mit Büroklammern zum Würfelmodell zusammen (Abb. 5).

Abb. 5: Modell aus DIN A6 Karten

Wenn alles sitzt, können die Büroklammern durch Stapelklammern ersetzt werden.

5 Origami-Modell

Zunächst eine theoretische Vorbereitung.

Wir vierteln zwei gegenüberliegende rechte Winkel des Origami-Quadrates (Abb. 6a).

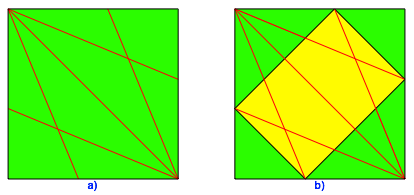
Abb. 6: Winkelhalbierende

Dann können wir ein Rechteck mit dem Seitenverhältnis (DIN-Format) einspannen (Abb. 6b).

In der Abbildung 6b sehen wir an den Quadratecken im Wechsel zwei große und zwei kleine rechtwinklig gleichschenklige Dreiecke. Wir falten nun die zwei kleinen hinein (Abb. 7a).

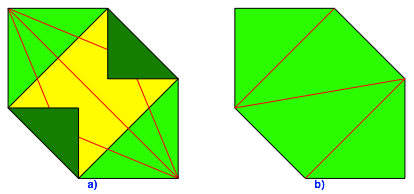
Abb. 7: Gleichseitiges Sechseck mit Winkeln 90° und 135°

Der Umriss der Figur ist ein gleichseitiges Sechseck. Dieses ist aber nicht gleichwinklig, sondern hat zwei rechte Winkel und vier Winkel von 135°. Das Sechseck ist also nicht regelmäßig.

Nun falten wir Linien gemäß Abbildung 7b. Diese Faltlinien sind als „Talfalten“ zu verstehen. Damit erhalten wir die Abwicklung eines (unregelmäßigen) Tetraeders. Dieses Tetraeder ist aber unser Orthoschem.

Nun zur Praxis.

Wir falten das Origami-Papier wie im Origami-Grundkurs längs der beiden Mittellinien. Dann Zerschneiden wir längs einer Mittellinie und bearbeiten jedes Teilstück einzeln weiter. (Abb. 8).

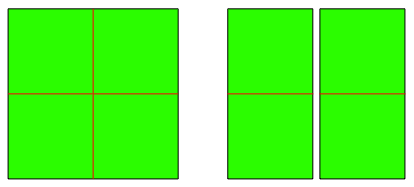
Abb. 8: Start

Wir falten die untere und die obere Hälfte in die Mitte hinein und erhalten so wieder ein kleines Quadrat (Abb. 9). Es ist doppellagig mit Schlitzen links und rechts. Dieses kleine Quadrat bearbeiten wir nun gemäß Abbildungen 6 und 7. Dabei unterscheiden sich dann die fertigen Modelle spiegelbildlich je nachdem, ob im kleinen Quadrat mit der Quadratdiagonalen von links oben nach rechts unten (wie in Abbildung 9 dargestellt) oder aber mit der Quadratdiagonalen von rechts oben nach links unten gearbeitet wird.

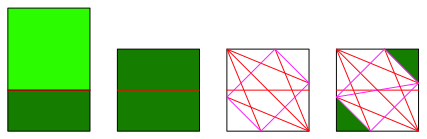
Abb. 9: Weiteres Vorgehen

Nun falten wir längs der magenta Faltlinien hoch und formen das Orthoschem. Die kleinen rechtwinklig gleichschenkligen Dreiecke können seitlich in die Schlitze der großen eingesteckt werden und dienen so als Verbindungslaschen. Das Modell hält ohne Leim. Eine der Kanten, nämlich die mittlere der drei kurzen Kanten, ist offen.

Die Abbildung 10 zeigt zwei spiegelbildliche Modelle.

Abb. 10: Orthoscheme

Drei linke und drei rechte Orthoscheme können zum Würfel gepackt werden (Abb. 11). Dabei können die Einzelteile mit einem Gummiband fixiert werden. Dieses läuft als regelmäßiges Sechseck in der Normalebne zur gemeinsamen Würfeldiagonale der sechs Bauteile.

Abb. 11: Würfel aus sechs Orthoschemen

Die Abbildung 12 zeigt denselben Würfel mit (beinahe) projizierender Würfeldiagonale.

Abb. 12: Über Eck

Vier linke und vier rechte Orthoscheme können zu einer Pyramide zusammengestellt werden (Abb. 13).

Abb. 13: Pyramide