Hans Walser, [20131210]

Origami und DIN-Format

Anregung: A. L., S.

1 Worum geht es?

Durch einen einfachen Faltprozess erhalten wir im Origami-Quadrat ein Rechteck im DIN-Format.

2 Faltvorgang

Wir vierteln zwei gegenüberliegende rechte Winkel des Origami-Quadrates (Abb. 1a).

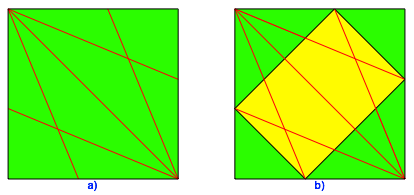
Abb. 1: Winkelhalbierende

Dann können wir ein Rechteck mit dem Seitenverhältnis (DIN-Format) einspannen (Abb. 1b).

3 Beweis

Die Winkelhalbierende im Dreieck teilt die Gegenseite im Verhältnis der anliegenden Seiten.

Daher ist in unserem Fall (Abb. 2):

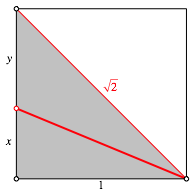
Abb. 2: Beweisfigur

Dieses Verhältnis überträgt sich auf das Seitenverhältnis des Rechteckes in Abbildung 1b.

Wegen x + y = 1 ergibt sich:

Für die Seiten a und b des Rechteckes erhalten wir:

Damir ergibt sich die Rechteckfläche:

4 Silbernes Rechteck und regelmäßiges Achteck

Wir finden im DIN-Rechteck der Abbildung 1b auch das so genannte Silberne Rechteck (Abb. 3).

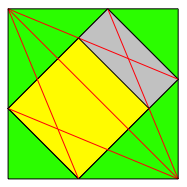
Abb. 3: Silbernes Rechteck

Das Silberne Rechteck entsteht als Restrechteck beim Abschneiden eines Quadrates von einem DIN-Rechteck. Es hat das Seitenverhältnis und den Diagonalen-Schnittwinkel 45°.

Wir vierteln alle vier rechten Winkel des Quadrates. Wir finden dabei nochmals das Silberne Rechteck (Abb. 4a) sowie ein regelmäßiges Achteck (Abb. 4b).

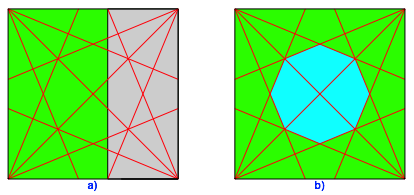
Abb. 4: Silbernes Rechteck und regelmäßiges Achteck

5 Schnittpunkte

Wir zeichnen nun in der Figur der Abbildung 4b zusätzlich ein Rechteck im DIN-Format gemäß Abbildung 1b ein (Abb. 5a).

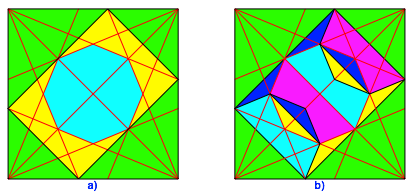
Abb. 5: Achteck und DIN-Rechteck

Zunächst stellen wir fest, dass zwei diametrale Achteckecken genau in den Mittelpunkten der langen Seiten des DIN-Rechteckes liegen. Dies lässt sich mit Teilverhältnissen und Strahlensätzen einsehen. Weiter ist der Flächeninhalt des Achteckes genau die Hälfte des Flächeninhaltes des DIN-Rechteckes. Die Abbildung 5b illustriert das mit einer Zerlegung.

6 Gleichseitiges Sechseck

In der Abbildung 1b sehen wir an den Quadratecken im Wechsel zwei große und zwei kleine rechtwinklig gleichschenklige Dreiecke. Wir falten nun die zwei kleinen hinein (Abb. 6a).

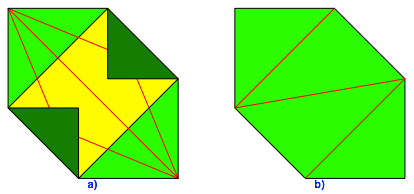
Abb. 6: Gleichseitiges Sechseck mit Winkeln 90° und 135°

Der Umriss der Figur ist ein gleichseitiges Sechseck. Dieses ist aber nicht gleichwinklig, sondern hat zwei rechte Winkel und vier Winkel von 135°. Das Sechseck ist also nicht regelmäßig.

Nun falten wir Linien gemäß Abbildung 6b. Diese Faltlinien sind als „Talfalten“ zu verstehen. Damit erhalten wir die Abwicklung eines (unregelmäßigen) Tetraeders. Ein Tetraeder dieser Art heißt Orthoschem; es ist die räumliche Verallgemeinerung des rechtwinklig gleichschenkligen Dreieckes. Es entsteht als konvexe Hülle dreier aufeinanderfolgender paarweise orthogonaler Würfelkanten (Abb. 7).

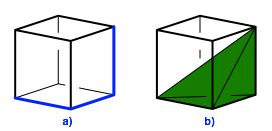
Abb. 7: Orthoschem

Da die diagonale Faltlinie im DIN-Rechteck der Abbildung 6b auf zwei verschiedene Arten gewählt werden kann, gibt es zwei zueinander spiegelbildliche Ausführungen des Orthoschems. Man kann den Würfel mit drei „linken“ und drei „rechten“ Orthoschems ausfüllen.

Wir verwenden nun das gleichseitige Sechseck der Abbildung 6 als Parkettstein.

Zunächst gibt es eine Parkettierung, welche ein affin verzerrtes Bild der regulären Hexagonalparkettierung (Bienenwabenmuster) ist (Abb. 8).

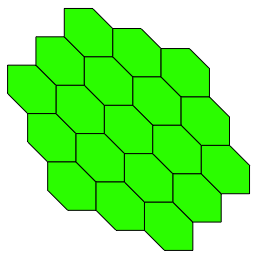
Abb. 8: Hexagonalparkettierung

Es gibt aber auch ein Parkett mit einer vierteiligen Drehsymmetrie und einer Singularität im Zentrum (Abb. 9). Das ist der einzige Punkt, in welchem vier Parkettsteine zusammenstoßen.

Abb. 9: Vierteilige Symmetrie

Das Ganze hat System und lässt sich verallgemeinern (Abb.10).

Abb.10: Verallgemeinerung

Literatur

Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-69-1.