Hans Walser, [20130407]

Die Mšndchen von Hšrhausen

Ausarbeitung einer Idee von R. L.

1        Das Mšndchen

Der Hypotenuse eines rechtwinklig gleichschenkligen Dreiecks setzen wir gemŠ§ Abbildung 1 ein Mšndchen auf.

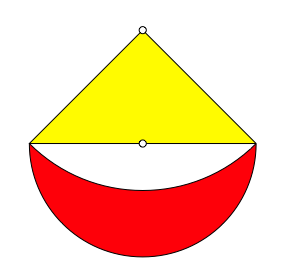
Abb. 1: Mšndchen. Rot = Gelb

Der Au§enrand des Mšndchens ist ein Bogen des Thaleskreises Ÿber der Hypotenuse des Dreieckes, der Innenrand ein Bogen mit dem Zentrum in der rechtwinkligen Dreiecksecke.

Das Mšndchen und das Dreieck haben denselben FlŠcheninhalt. Der Beweis verlŠuft rechnerisch, wobei wir fŸr das Dreieck die KathetenlŠnge 1 wŠhlen. Es ist zunŠchst fŸr die DreiecksflŠche:

 

Weiter erhalten wir fŸr die MšndchenflŠche:

 

 

 

2        Unterteilung des Dreiecks

Wir unterteilen das Dreieck gemŠ§ Abbildung 2 und setzen einem der beiden Teildreiecke ebenfalls ein Mšndchen auf.

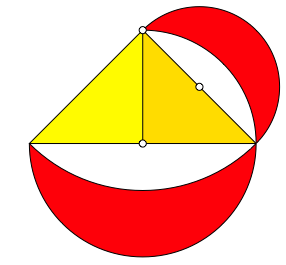
Abb. 2: Noch ein Mšndchen

Bevor wir mit der Unterteilung entsprechend weiterfahren, einige Bemerkungen.

Der FlŠcheninhalt des neuen Mšndchens ist halb so gro§ wie der FlŠcheninhalt des ersten Mšndchens. Dies ergibt sich daraus, dass das zugehšrige rechtwinklig gleichschenklige Dreieck den halben FlŠcheninhalt des ursprŸnglichen Dreiecks hat. Das gibt Anlass zur Figur der Abbildung 3. Es handelt sich dabei um einen Sonderfall der so genannten Mšndchen des Hippokrates (vgl. [Heinrich/Schmitz/Walser 1999]).

 

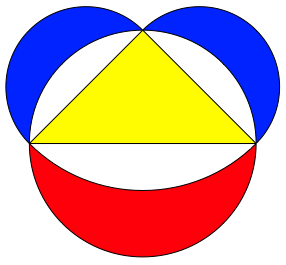
Abb. 3: Blau = Rot = Gelb

Der Innenrand des kleinen Mšndchens der Abbildung 2 liegt auf demselben Kreis wie der Au§enrand des gro§en Mšndchens. Zusammen bilden die beiden RŠnder einen Dreiviertel-Kreis, in der Abbildung 4 blau eingezeichnet.

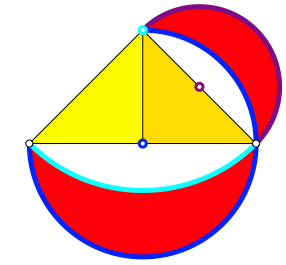
Abb. 4: Kreisbšgen

Der hellblaue Innenrand des gro§en Mšndchens geht glatt in den violetten Au§enrand des kleinen Mšndchens Ÿber. Glatt hei§t, dass wir im †bergangspunkt keinen Richtungssprung haben. Da die beiden Kreisbšgen aber verschiedene Radien und verschiedene Zentren haben, ergibt sich ein abrupter KrŸmmungssprung. Die KrŸmmung wird beim †bergang von hellblau zu violett verdoppelt. Ein schnelles Fahrzeug kšnnte beim †bergang vom hellblauen Bogen zum violetten Bogen aus der Spur kippen. Als Trasse fŸr einen VerkehrstrŠger lebensgefŠhrlich.

3        Iteration

Wir unterteilen das Dreieck weiter gemŠ§ Abbildung 5.

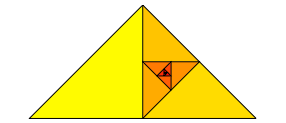
Abb. 5: Iteration der Unterteilung

Es ergibt sich eine eckige Spirale mit einem Grenzpunkt. Der Grenzpunkt passt in einen FŸnftel-Raster (Abbildung 6).

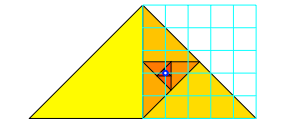
Abb. 6: FŸnftel

Nun zeichnen wir auch noch die Mšndchen zu den Dreiecken (Abbildung 7).

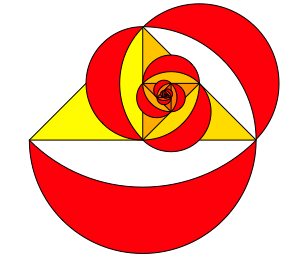
Abb. 7: Dreiecke mit Mšndchen

Addieren wir vom zweiten Mšndchen an die FlŠcheninhalte der Mšndchen, erhalten wir den FlŠcheninhalt des ersten Mšndchens.

In der Abbildung 8 sind die Dreiecke weggelassen.

Abb. 8: Mšndchen

Die Randlinien der Mšndchen bilden zwei logarithmische Pseudospiralen (Abb. 9).

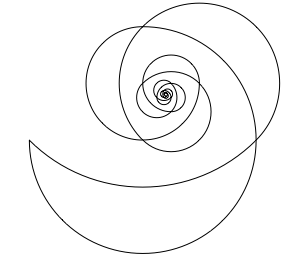
Abb. 9: Zwei Spiralen

Die Spiralen sind aus Dreiviertelkreisen zusammengesetzt. Die Figur erinnert an den Kornkreis von Hšrhausen (Abb. 10). Im Literaturverzeichnis diverse Artikel aus der Thurgauer Zeitung Ÿber diesen Kornkreis.

Abb. 10: Kornkreis von Hšrhausen, 18. 7. 2009, Foto Beni Sidler (Nachzeichnung des Autors)

Eine einzelne Spirale sieht recht unnatŸrlich aus (Abb. 11). Das liegt an den KrŸmmungssprŸngen. Bei jedem †bergangspunkt wird die KrŸmmung verdoppelt.

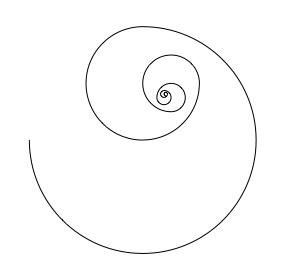
Abb. 11: Eine der beiden Spiralen

Die Abbildung 12 zeigt im Vergleich dazu eine echte logarithmische Spirale (vgl. [Heitzer 1998]). Die KrŸmmung nimmt gegen innen kontinuierlich zu.

Abb. 12: Logarithmische Spirale

In der Abbildung 13 sind die beiden Mšndchenspiralen zusammen mit der logarithmischen Spirale eingezeichnet.

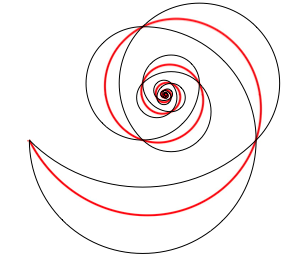
Abb. 13: Vergleich mit der logarithmischen Spirale

Die Mšndchenspiralen pendeln auf beide Seiten der logarithmischen Spirale.


4        Verallgemeinerung

Wir sind in unserer Konstruktion von einem rechtwinklig gleichschenkligen Dreieck ausgegangen. Wir kšnnen aber auch mit einem beliebigen gleichschenkligen Dreieck starten (Abb. 14). Das Startdreieck habe die SchenkellŠnge  und den Spitzenwinkel .

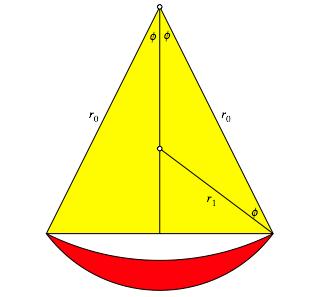
Abb. 14: Beliebiges gleichschenkliges Dreieck

In dieses Dreieck zeichnen wir den Umkreismittelpunkt. FŸr den Umkreisradius  erhalten wir:

 

 

 

Das Startmšndchen hat den Au§enbogen mit dem Radius  und dem Zentrum im Umkreismittelpunkt des gleichschenkligen Dreieckes und den Innenbogen mit dem Radius  und dem Zentrum in der Spitze des gleichschenkligen Dreieckes.


Nun passen wir ein weiteres zum Startdreieck Šhnliches Dreieck ein gemŠ§ Abbildung 15.

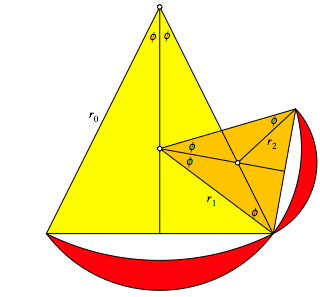
Abb. 15: Einpassen eines weiteren Dreieckes

Das neue Dreieck hat die SchenkellŠnge  und ist gegenŸber dem Startdreieck um  verdreht. Der Au§enrand des Startmšndchens und der Innenrand des neuen Mšndchens liegen auf demselben Kreis. Der Innenrand des Startmšndchens geht glatt in den Au§enrand des neuen Mšndchens Ÿber. Wir haben aber einen KrŸmmungssprung mit dem Faktor .


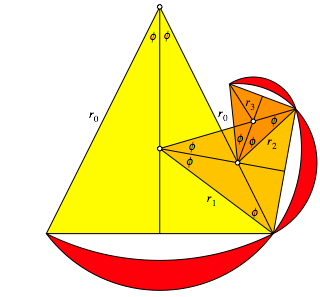
Die Abbildung 16 zeigt den nŠchsten Schritt.

.

Abb. 16: NŠchster Schritt

Schlie§lich kšnnen wir ad infinitum iterieren (Abb. 17).

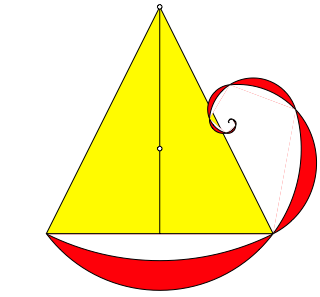
Abb. 17: Iteration

5        SonderfŠlle

Nachdem wir mit einem beliebigen gleichschenkligen Dreieck starten kšnnen, ergeben sich weitere reizvolle SpezialfŠlle.

5.1      Der Clan des gleichseitigen Dreiecks

5.1.1    Gleichseitiges Dreieck

Wir starten mit einem gleichseitigen Dreieck (Abb. 18).

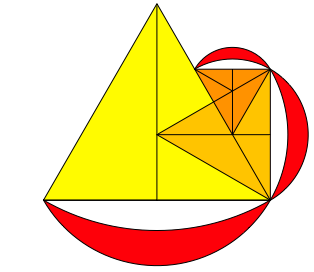
Abb. 18: Gleichseitiges Dreieck

Aufeinanderfolgende Dreiecke und Mšndchen sind jeweils um 90¡ verdreht und mit dem Faktor  gestreckt, inhaltlich also geschrumpft.


Die Abbildung 19 zeigt die Iteration.

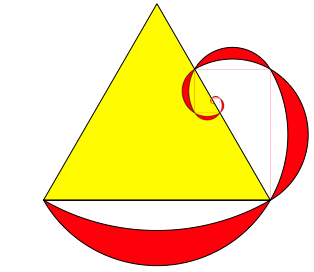
Abb. 19: Iteration

Der Grenzpunkt der Spirale ist ein Seitenmittelpunkt des Startdreieckes.

5.1.2    Spitzenwinkel 120¡

Das Startdreieck hat an der Spitze einen Winkel von 120¡. Die Abbildung 20 zeigt die Situation.

Abb. 20: Startsituation

FŸr den ersten Schritt ergibt sich der Streckfaktor . Das nŠchste Dreieck und das zugehšrige Mšndchen sind also gleich gro§ (Abb. 21).

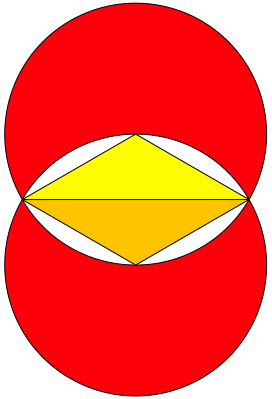
Abb. 21: Erster Schritt

Wir erhalten also eine stabile Situation ohne Spirale.

5.2      Goldener Schnitt

Es werden Startdreiecke untersucht, welche mit dem Goldenen Schnitt zusammenhŠngen. . †ber den Goldenen Schnitt vgl. [Walser 2013].

5.2.1    Spitzes Goldenes Dreieck

Das Spitze Goldene Dreieck hat an der Spitze einen Winkel von 36¡. SchenkellŠnge und BasislŠnge stehen im VerhŠltnis des Goldenen Schnittes, und zwar ist:

 

 

 

Das Spitze Goldene Dreieck tritt im regelmŠ§igen FŸnfeck auf. Die Abbildung 22 zeigt die ersten drei Schritte, die Abbildung 23 die Iteration.

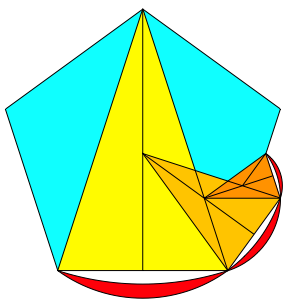
Abb. 22: Spitzes Goldenes Dreieck

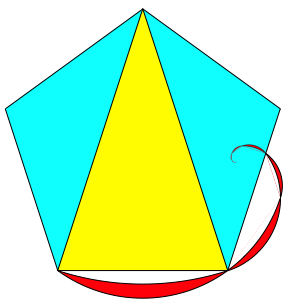
Abb. 23: Iteration

5.2.2    Das Sektordreieck im FŸnfeck

Das Sektordreieck im regelmŠ§igen FŸnfeck hat den Spitzenwinkel 72¡. FŸr den Streckfaktor erhalten wir , also den Kehrwert des Goldenen Schnittes. Die Abbildung 24 zeigt den Start, die Abbildung 25 die Spirale. Eine neue Form der Goldenen Spirale.

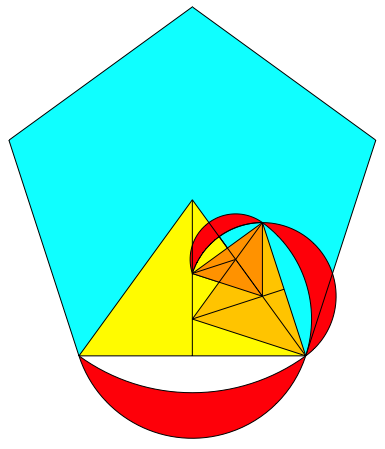
Abb. 24: Sektordreieck des FŸnfeckes

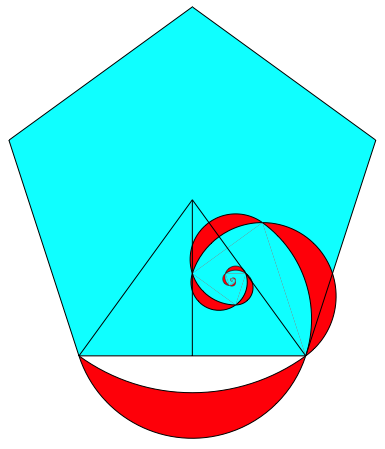
Abb. 25: Spirale

In der Abbildung 26 wird die fŸnfteilige Drehsymmetrie ausgelebt.

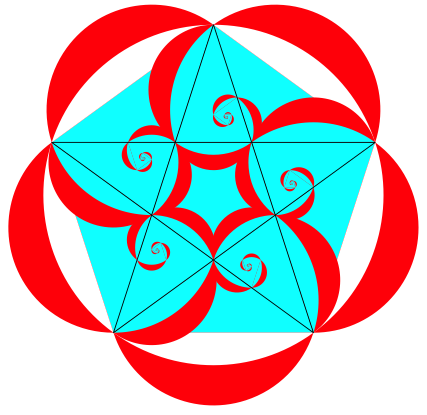
Abb. 26: FŸnfteilige Drehsymmetrie

5.2.3    Stumpfes Goldenes Dreieck

Das Stumpfe Goldene Dreieck hat an der Spitze einen Winkel von 108¡. BasislŠnge und SchenkellŠnge stehen im VerhŠltnis des Goldenen Schnittes, und zwar ist:

 

 

 

Wir haben also im Vergleich zum Spitzen Goldenen Dreieck das umgekehrte VerhŠltnis. Die Abbildung 27 zeigt die ersten drei Schritte, die Abbildung 28 die Iteration. Wir haben gewaltige †berlappungen.

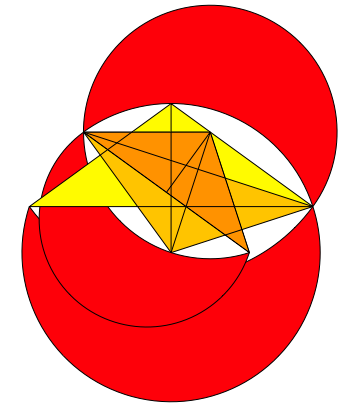
Abb. 27: Stumpfes Goldenes Dreieck

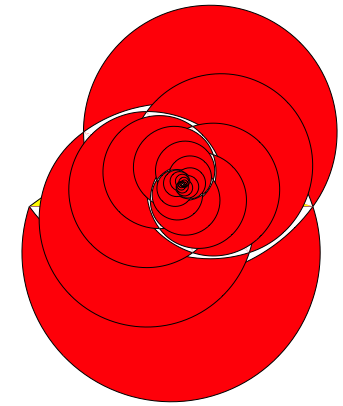
Abb. 28: Iteration

5.3      Der Grenzfall

Wir haben gesehen, dass ein rechtwinklig gleichschenkliges Startdreieck zu einer nicht Ÿberlappenden Spirale fŸhrt (Abb. 8), wŠhrend ein Winkel von 108¡ an der Spitze schon zu gewaltigen †berlappungen Anlass gibt (Abb. 28). Daher muss es zwischen 90¡ und 108¡ einen Grenzfall geben, bei dem sich die Spirale selbst berŸhrt, aber nicht Ÿberlappt. Dieser Grenzfall lŠsst sich nicht elementar berechnen (jedenfalls ist es mir nicht gelungen), mit dem numerischen Verfahren von Newton-Raphson erhielt ich den NŠherungswert 100.8406064¡. Die Abbildung 29 zeigt die Startsituation. Wir sehen die BerŸhrung mit dem ŸbernŠchsten Mšndchen.

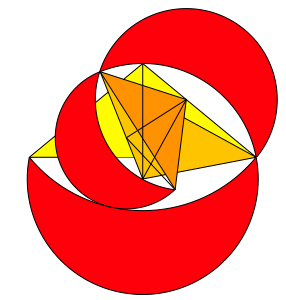
Abb. 29: Startsituation

Die Abbildung 30 schlie§lich zeigt die sich selbst berŸhrende Spirale.

Abb. 30: Spirale

6        Weitere Verallgemeinerung

In den bisherigen Beispielen sind wir von einem gleichschenkligen Dreieck ausgegangen. Bis auf Skalierung haben wir dabei einen freien Parameter, in unserer Notation den Winkel  an der Spitze des Dreiecks.

Wir werden nun so verallgemeinern, dass wir bis auf Skalierung drei freie Parameter haben. Dabei gehen wir schrittweise vor.

6.1      Die Mittellinie

Jede technische Zeichnung geht von der Mittellinie aus.

Handbuch fŸr Ingenieure

In unserem Fall ist die Mittellinie aus Kreisbšgen zusammengesetzt. Wir beginnen mit einem Kreisbogen mit dem …ffnungswinkel  (Abb. 31). Dieser …ffnungswinkel  ist der erste Parameter.

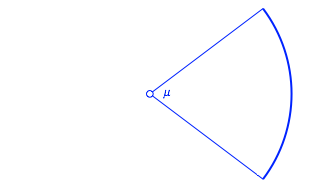
Abb. 31: Startbogen

Als zweiten freien Parameter wŠhlen wir einen Streckfaktor s. Damit die anvisierte Spirale einwŠrts lŠuft, wŠhlen wir . Nun Ÿben wir auf den Startbogen eine Drehstreckung mit dem Drehwinkel  und dem Streckfaktor s aus und heften das Bild gemŠ§ Abbildung 32 an den Startbogen an. Im Beispiel der Abbildung 32 wurde  gewŠhlt. Im †bergangspunkt der beiden Bšgen haben wir einen glatten RichtungsŸbergang, aber einen KrŸmmungssprung. Die KrŸmmung nimmt um den Faktor  zu.

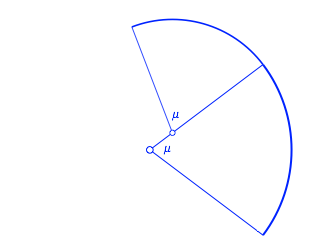
Abb. 32: Der nŠchste Bogen

Das Vorgehen kann iteriert werden. Es ergibt sich eine logarithmische Pseudospirale (Abb. 33).

 

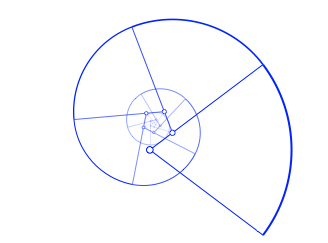
Abb. 33: Spirale

Diese Spirale ist ein Beispiel eines so genannten Korbbogens (vgl. [Giering 1992] und [Walser 1996]). FŸr  und  ergibt sich die klassische Spiralen-Figur im Goldenen Rechteck (Abb. 34).

Abb. 34: Logarithmische Pseudospirale im Goldenen Rechteck

Die Korbbogen-Spiralen werden wir nun als Mittellinien unserer Mšndchen verwenden.

6.2      Mšndchen

Wir wŠhlen einen Winkel , der zum Winkel an den Mšndchenspitzen werden soll. Dieser Winkel  ist der dritte freie Parameter. Dann konstruieren wir gemŠ§ Abbildung 35 das Startmšndchen.

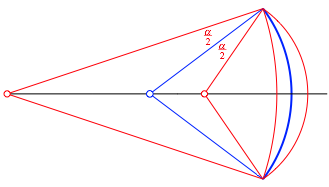
Abb. 35: Startmšndchen

Der blaue Startsektor ist die Winkelhalbierendenfigur zum Startmšndchen. Wir kšnnen nun weitere Mšndchen ansetzen (Abb. 36).

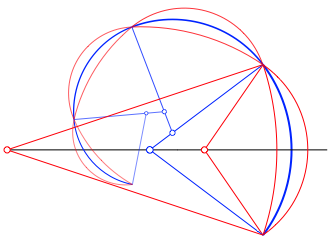
Abb. 36: Weitere Mšndchen

Der Innenrand eines Mšndchens geht glatt in den Au§enrand des Folgemšndchens Ÿber und umgekehrt.

Die Abbildung 37 zeigt die Mšndchenspirale.

Abb. 37: Mšndchenspirale

Erinnerung: Im Abschnitt 4 waren wir von einem gleichschenkligen Dreieck mit dem Winkel  an der Spitze ausgegangen. Nach dem Konzept in diesem Abschnitt gelten fŸr die drei Parameter dann folgende Beziehungen:

 

 

 

6.3      Zweiecke

Wir kšnnen die Mšndchen durch konvexe, von zwei Kreisbšgen berandete Zweiecke ersetzen gemŠ§ Abbildung 38.

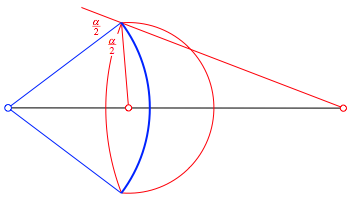
Abb. 38: Zweieck

Die Abbildung 39 zeigt die zugehšrige Spirale. Die Randkreise gehen glatt ineinander Ÿber, aber in den †bergangspunkten wechseln die KrŸmmung sogar das Vorzeichen (Wendepunkte).

Abb. 39: Zweieckspirale

Literatur

[Borkert 2009]            Borkert, Stefan: Das RŠtsel von Hšrhausen. Thurgauer Zeitung, 22. Juli 2009

[Engelhard 2009]        Engelhard, Imarc: Die kleinen grŸnen MŠnnchen warens nicht. Thurgauer Zeitung, 25. Juli 2009

[Gerteis 2009]            Gerteis, Sarah: Es muss etwas hinter Kornkreisen stecken. Thurgauer Zeitung, 21. Juli 2009

[Gerteis 2009]            Gerteis, Sarah: Tendiere auf menschliches Dazutun. Thurgauer Zeitung, 22. Juli 2009

[Giering 1992]            Giering, Oswald: Zur Geometrie der Polygon-Korbbšgen. PM, Praxis der Mathematik (34), 1992, S. 245-248

[Heinrich/Schmitz/Walser 1999]       Heinrich, Frank / Schmitz, Michael / Walser, Hans: Verallgemeinerungen der ÓMšndchen des HippokratesÓ. MNU Der mathematische und naturwissenschaftliche Unterricht 52/5, 1999, 264-270

[Heitzer 1998]            Heitzer, Johanna: Spiralen, ein Kapitel phŠnomenaler Mathematik. Leipzig: Klett 1998. ISBN 3-12-720044-7

[Sandl 2009]               Sandl, Iida: Der schšnste Kornkreis ist platt. Thurgauer Zeitung, 7. August 2009

[Sandl 2009]               Sandl, Iida: Im Kornkreis den Aliens auf der Spur. Thurgauer Zeitung, 22. Juli 2009

[Walser 1996]            Walser, Hans: Geschlossene Korbbšgen. PM, Praxis der Mathematik (38), 1996, 169-172

[Walser 2013]            Walser, Hans: Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-85-1