Hans Walser, [20050829a], [20171103]

Magische Kreise

1 Die Probleme

1.1 Drei Kreise

In die quadratischen Felder sind die Zahlen 1 bis 6 so einzusetzen, dass auf jedem Kreis die Summe gleich ist.

Abb. 1: Drei Kreise

1.2 Vier Kreise

In die Rhomben-Felder sind die Zahlen 1 bis 12 so einzusetzen, dass auf jedem Kreis die Summe gleich ist.

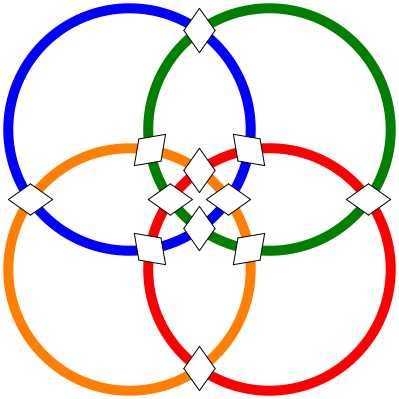
Abb. 2: Vier Kreise

1.3 Sechs Kreise

In die Felder (Quadrate und Sechsecke) sind die Zahlen 1 bis 14 so einzusetzen, dass auf jedem Kreis die Summe gleich ist.

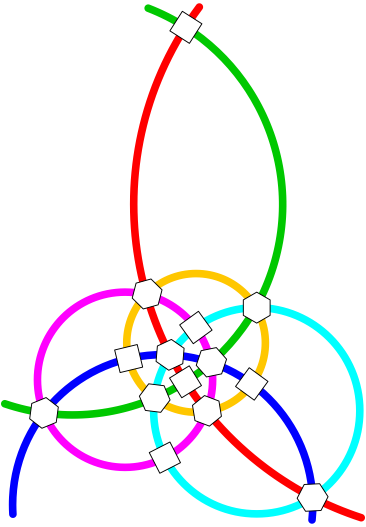
Abb. 3: Sechs Kreise

1.4 Sieben Kreise

Gesucht sind 18 auf einander folgende ungerade Zahlen, so dass auf jedem Kreis die Summe gleich ist.

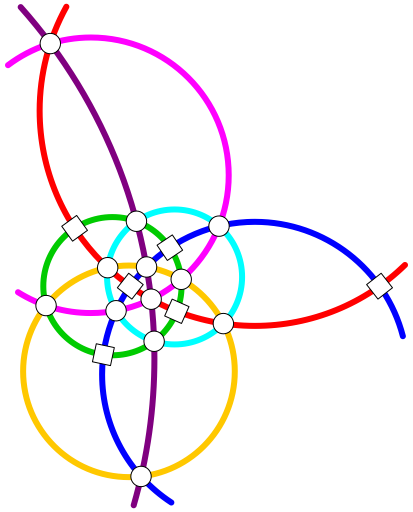
Abb. 4: Sieben Kreise

1.5 Nochmals ein Beispiel mit sieben Kreisen

Gesucht sind 18 auf einander folgende ganze Zahlen (sie dürfen auch negativ sein), so dass auf jedem Kreis die Summe gleich ist.

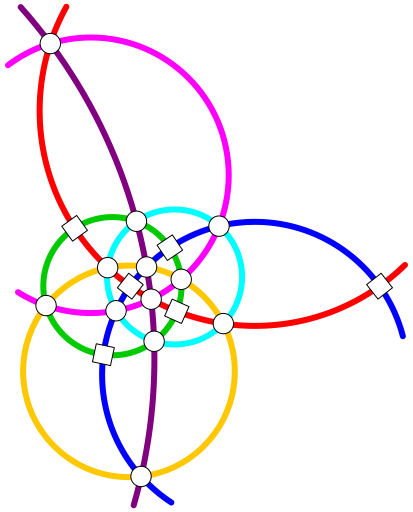
Abb. 5: Nochmals sieben Kreise

2 Bearbeitungen und Lösungen

2.1 Drei Kreise

Wir machen eine Mittel-Überlegung.

Zunächst ist 1 + 2 + 3 + 4 + 5 + 6 = 21. Da jeder Kreis zwei Drittel der sechs Felder begreift, muss auf jedem Kreis die Kreissumme 14 sein. Da weiter zwei Kreise genau zwei Felder gemeinsam haben, muss in diesen beiden Feldern die Summe 7 sein. Wir können also mit der 1 irgendwo beginnen und müssen dann im Gegenfeld die 6 setzen. Und so weiter. Die Abbildung 6 zeigt eine mögliche Lösung.

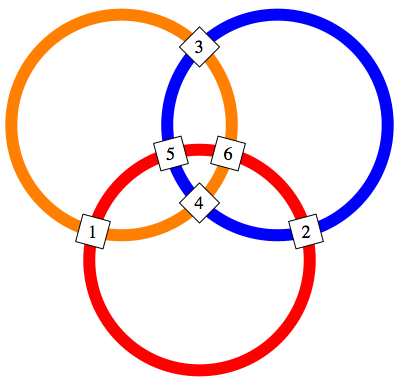
Abb. 6: Drei Kreise

Man vergleiche damit die Verteilung der Augenzahlen auf einem Spielwürfel.

2.2 Vier Kreise

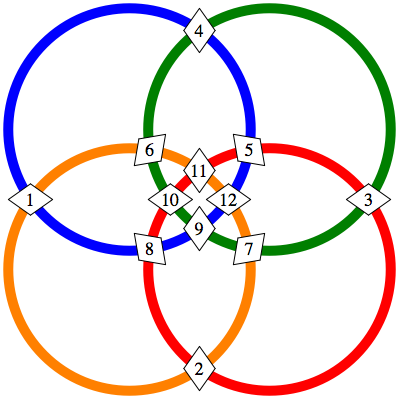
Abb. 7: Vier Kreise

Die Überlegung läuft analog zum Beispiel mit drei Kreisen. Die Kreissumme ist 39.

2.3 Sechs Kreise

Hier gibt es mehrere Lösungen, nicht nur, was die Verteilung der Zahlen betrifft, sondern auch bei der Kreissumme. Dies deshalb, weil es Felder in Kreuzungspunkten von zwei Kreisen und Felder in Kreuzungspunkten von drei Kreisen gibt.

Bei der Lösung der Abbildung 8 haben wir die Kreissumme 41.

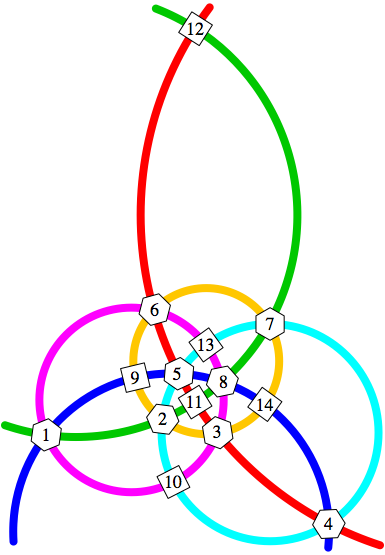
Abb. 8: Kreissumme 41

Bei der Lösung der Abbildung 9 haben wir die Kreissumme 45.

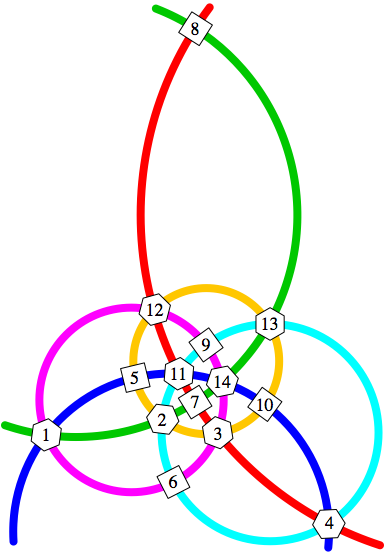
Abb. 9: Kreissumme 45

Bei der Lösung der Abbildung 10 ergibt sich die Kreissumme 49. Ich weiß nicht, ob es noch weitere Lösungen gibt.

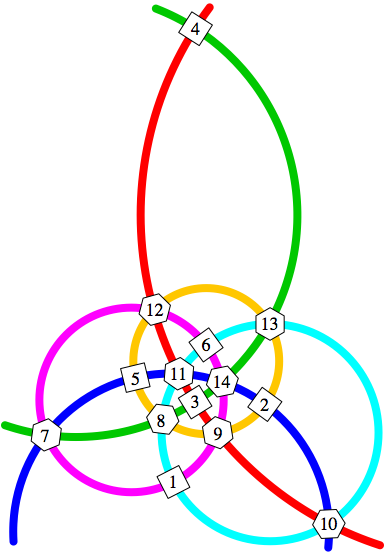
Abb. 10: Kreissumme 49

2.4 Sieben Kreise

Im Beispiel der Abbildung 11 kommen genau die ungeraden Zahlen 13, 15, ... , 45, 47 vor. Die Kreissumme ist 216.

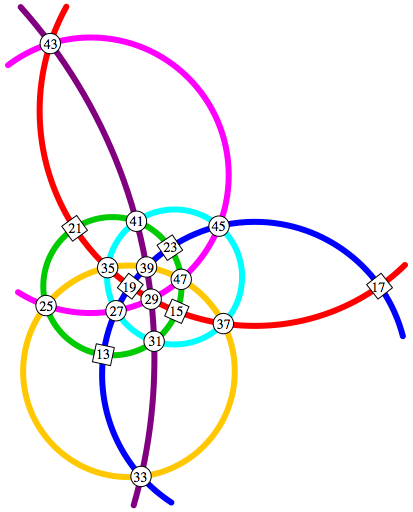
Abb. 11: Kreissumme 216

2.5 Noch ein Beispiel mit sieben Kreisen

Im Beispiel der Abbildung 12 erscheinen genau die 18 aufeinander folgenden ganzen Zahlen –1, 0, 1, 2, 3, ... , 16. Die Kreissumme ist 54.

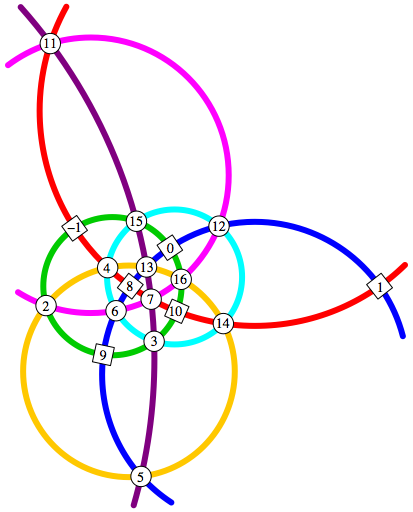
Abb. 12: Kreissumme 54

3 Geometrie der Kreise

Die Kreise schneiden sich unter bestimmten regelmäßigen Winkeln. Der Hintergrund ist die stereografische Projektion von symmetrischen Großkreisen auf der Kugel.

3.1 Drei Kreise

Die drei paarweise orthogonalen Großkreise der Abbildung 13 ergeben bei geeigneter stereografischer Projektion die drei Kreise in der Position der Abbildungen 1 und 6.

Abb. 13: Drei paarweise orthogonale Großkreise

3.2 Vier Kreise

Die vier Großkreise der Abbildung 14 schneiden sich unter spitzen Winkel von:

(1)

Abb. 14: Schnittwinkel ≈ 70.53°

Dies führt zu den vier Kreisen der Abbildungen 2 und 7.

3.3 Sechs Kreise

Wenn wir beim Kugelmodell der Abbildung 13 die Winkelhalbierenden Kreise einfügen und dann die ursprünglichen drei Kreise entfernen, bleibt ein Modell mit sechs Großkreisen übrig. Diese schneiden sich entweder orthogonal (6 Schnittpunkte) oder unter Winkeln von 60° (8 Schnittpunkte).

3.4 Sieben Kreise

Die Abbildung 15 zeigt ein Kugelmodell mit 7 Großkreisen. Das Modell ist eine Überlagerung der Modelle der Abbildungen 13 und 14.

Abb. 15: Sieben Großkreise

Wir haben zwei verschiedene Großkreistypen. Daher ist auch das Zahlenrätsel nicht ganz einfach.