Hans Walser, [20171019]

Magische Quadrate ungerader Seitenlänge

Anregung: Euler (1782)

1 Worum geht es?

Zu einer gegebenen ungeraden Zahl u wird ein magisches Quadrat mit der Seitenlänge u konstruiert.

2 Das Vorgehen

Wir illustrieren das Vorgehen exemplarisch für u = 7.

2.1 Buchstaben

Zunächst nehmen wir die ersten u kleinen Buchstaben des Alphabets und markieren den Buchstaben in der Mitte (Abb. 1a).

Abb. 1: Buchstaben

Analog verfahren wir mit großen Buchstaben (Abb. 1b).

2.2 Im Quadratraster

Im u×u-Quadratraster setzen wir in den Feldern der Diagonalen von links oben nach rechts unten je den in der Abbildung 1b rot markierten mittleren großen Buchstaben ein (Abb. 2).

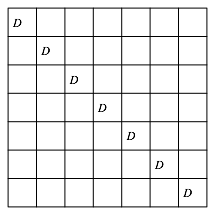
Abb. 2: Diagonale im Quadratraster

Wir ergänzen in jeder Zeile mit großen Buchstaben in alphabetischer Reihenfolge von links nach rechts (Abb. 3). Wenn wir beim letzten Buchstaben der Liste der Abbildung 1b angekommen sind, fahren wir mit A weiter. Wenn wir am rechten Rand des Quadratrasters ankommen, fahren wir links mit dem nächsten Buchstaben weiter.

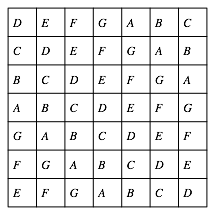
Abb. 3: Alphabetische Ergänzung

Der durch die Startdiagonale bedingte Versatz hat zur Folge, dass in jeder Zeile und in jeder Spalte jeder große Buchstabe genau einmal vorkommt.

Nun setzen wir in der anderen Diagonale (von rechts oben nach links unten) je den rot markierten mittleren kleinen Buchstaben der Abbildung 1a dazu (Abb. 4).

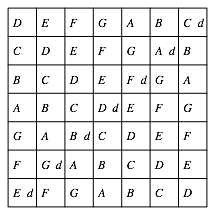
Abb. 4: Zweite Diagonale

Schließlich ergänzen wir die kleinen Buchstaben in jeder Spalte von oben nach unten in alphabetischer Reihenfolge (Abb. 5).

Abb. 5: Ergänzung mit kleinen Buchstaben

Wir haben jetzt in jeder Spalte und in jeder Zeile jeden kleinen Buchstaben genau ein Mal.

3 Zahlwerte

Wir ordnen den Buchstaben Zahlen zu gemäß Abbildung 6. Den kleinen Buchstaben ordnen wir der Reihe nach die Zahlen 0, ... , u – 1 zu, den großen Buchstaben das u-fache davon.

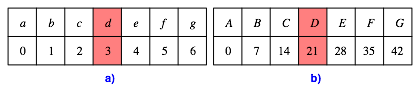
Abb. 6: Buchstaben und Zahlen

Nun setzen wir in jedem Feld die Summe der Zahlwerte des großen und des kleinen Buchstabens gemäß den Tabellen der Abbildung 6 ein. Für das Feld links oben haben wir zum Beispiel D + e = 21 + 4 = 25. So erhalten wir ein magisches Quadrat (Abb. 7).

25	33	41	42	1	9	17
19	27	28	36	44	3	11
13	14	22	30	38	46	5
0	8	16	24	32	40	48
43	2	10	18	26	34	35
37	45	4	12	20	21	29
31	39	47	6	7	15	23

Abb. 7: Magisches Quadrat

4 Warum funktioniert das?

4.1 Rechnerische Vorbereitungen

Zum rot markierten kleinen Buchstaben in der Mitte der Abbildung 1a gehört der Wert .

Die Summe s aller Werte der kleinen Buchstaben der Abbildung 1a ist:

(1)

Für unser Beispiel u = 7 erhalten wir s = 21. Das ist genau der rot unterlegte Wert in der Abbildung 1b.

Zum rot markierten großen Buchstaben in der Mitte der Abbildung 1b gehört der Wert .

Die Summe S der Werte der großen Buchstaben der Abbildung 1b ist:

(2)

Für unser Beispiel u = 7 erhalten wir S = 147.

Weiter können wir jede Zahl zwischen 0 und u² – 1 eindeutig als Summe eines großen und eines kleinen Zahlwertes darstellen. Beispiel: 37 = 35 + 2 = F + c.

4.2 Alle Zahlen kommen vor

Auf Grund unserer Konstruktion kommt jede mögliche Buchstabenkombination eines großen mit einem kleinen Buchstaben genau einmal. Umgekehrt gehört zu jeder Zahl zwischen 0 und u² – 1 eine eindeutig bestimmte Buchstabenkombination.

Wer lieber die Zahlen 1 bis u² im magischen Quadrat hat, kann einfach in jedem Feld eins dazuzählen. Allerdings werden dann gewisse schöne Eigenschaften weniger gut sichtbar.

4.3 Zeilen- und Spaltensummen

In jeder Zeile kommt jeder große und jeder kleine Buchstabe genau einmal vor. Somit ist wegen (1) und (2) die Zeilensumme Z gleich S + s, also konstant. Es ist:

(3)

Wir können das nachprüfen. Für die Summe T aller Zahlen von 0 bis u² – 1 gilt:

(4)

Da wir u Zeilen haben, ist die Zeilensumme Z:

(5)

Für die Spaltensumme überlegen wir analog. Die Spaltensumme ist ebenfalls Z.

4.4 Diagonalensummen

In der Diagonale von links oben nach rechts unten haben wir zwar ebenfalls alle kleinen Buchstaben mit dem Gesamtwert s. Hingegen kommt ausschließlich und damit u mal der mittlere große Buchstabe der Abbildung 1b vor. Dieser hat den Wert . Da dieser Wert u mal vorkommt, haben wir in dieser Diagonale für die großen Buchstaben den Gesamtwert:

(6)

Somit ist die Gesamtsumme in dieser Diagonale ebenfalls S + s = Z.

In der Diagonale von rechts oben nach links unten läuft es analog. Zunächst haben wir alle großen Buchstaben mit dem Gesamtwert S. Weiter kommt u mal die mittlere Zahl in der Abbildung 1a mit dem Wert vor, also insgesamt:

(7)

Wir haben also ebenfalls die Gesamtsumme S + s = Z.

5 Formel

Wir nummerieren die Zeilen (Abb. 5) von oben nach unten mit i = 1, ... , u und die Spalten von links nach recht mit j = 1, ... , u.

Wir suchen nach einer Formel für die Zahl im Feld (i, j), geschrieben .

Dazu untersuchen wir zunächst die Änderungen von f bei einem Zuwachs von i oder j um +1.

Eine Zuwachs von +1 bei j führt bei den großen Buchstaben zum nächsten Buchstaben im Alphabet, also zu einem Zuwachs von +u für f, da die Werte der großen Buchstaben in Schritten von u zunehmen. Eine Ausnahme ist die Situation, wenn wir beim letzten Buchstaben sind und zu A zurückmüssen. Wir können das regeln, indem wir bei j modulo u arbeiten.

Eine Zuwachs von +1 bei i führt bei den großen Buchstaben zum vorhergehenden Buchstaben. Wenn wir schon bei A, ergibt sich ein Sprung zum letzten Buchstaben. Auch das können wir regeln, indem wir bei i modulo u arbeiten.

Diese Zuwachsüberlegungen zeigen, dass der die großen Buchstaben betreffende Teil der gesuchten Formel additiv ist und zwar von der Form

(8)

ist mit einer noch offenen Justierung. Diese finden wir, indem wir für i und j ein spezielles Zahlenpaar, zum Beispiel (1,1), einsetzen. Damit finden wir für den die großen Buchstaben betreffenden Teil die Formel:

(9)

Bei den kleinen Buchstaben ist der Zuwachs in beiden Richtungen positiv (i wächst nach unten!). Damit erhalten wir zusammen mit der Justierung für diesen Teil:

(10)

Somit haben wir die Formel:

(11)

Im Folgenden Beispiele.

6 Beispiele

Es wird das magische Quadrat und das zugehörige Histogramm angegeben. Die Histogramme sind mit dem Faktor unterhöht.

6.1 u = 3

5	6	1
0	4	8
7	2	3

Abb. 8b: u = 3

Abb. 8b: Histogramm

6.2 u = 5

13	19	20	1	7
9	10	16	22	3
0	6	12	18	24
21	2	8	14	15
17	23	4	5	11

Abb. 9a: u = 5

Abb. 9b: Histogramm

6.3 u = 7

25	33	41	42	1	9	17
19	27	28	36	44	3	11
13	14	22	30	38	46	5
0	8	16	24	32	40	48
43	2	10	18	26	34	35
37	45	4	12	20	21	29
31	39	47	6	7	15	23

Abb. 10a: u = 7

Abb. 10b: Histogramm

6.4 u = 9

41	51	61	71	72	1	11	21	31
33	43	53	54	64	74	3	13	23
25	35	36	46	56	66	76	5	15
17	18	28	38	48	58	68	78	7
0	10	20	30	40	50	60	70	80
73	2	12	22	32	42	52	62	63
65	75	4	14	24	34	44	45	55
57	67	77	6	16	26	27	37	47
49	59	69	79	8	9	19	29	39

Abb. 11a: u = 9

Abb. 11b: Histogramm

6.5 u = 11

61	73	85	97	109	110	1	13	25	37	49
51	63	75	87	88	100	112	3	15	27	39
41	53	65	66	78	90	102	114	5	17	29
31	43	44	56	68	80	92	104	116	7	19
21	22	34	46	58	70	82	94	106	118	9
0	12	24	36	48	60	72	84	96	108	120
111	2	14	26	38	50	62	74	86	98	99
101	113	4	16	28	40	52	64	76	77	89
91	103	115	6	18	30	42	54	55	67	79
81	93	105	117	8	20	32	33	45	57	69
71	83	95	107	119	10	11	23	35	47	59

Abb. 12a: u = 11

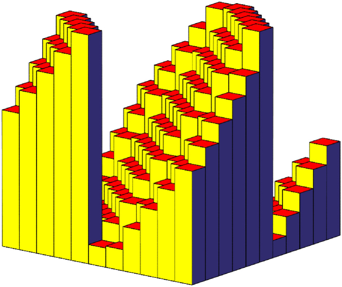
Abb. 12b: Histogramm

6.6 u = 13

85	99	113	127	141	155	156	1	15	29	43	57	71
73	87	101	115	129	130	144	158	3	17	31	45	59
61	75	89	103	104	118	132	146	160	5	19	33	47
49	63	77	78	92	106	120	134	148	162	7	21	35
37	51	52	66	80	94	108	122	136	150	164	9	23
25	26	40	54	68	82	96	110	124	138	152	166	11
0	14	28	42	56	70	84	98	112	126	140	154	168
157	2	16	30	44	58	72	86	100	114	128	142	143
145	159	4	18	32	46	60	74	88	102	116	117	131
133	147	161	6	20	34	48	62	76	90	91	105	119
121	135	149	163	8	22	36	50	64	65	79	93	107
109	123	137	151	165	10	24	38	39	53	67	81	95
97	111	125	139	153	167	12	13	27	41	55	69	83

Abb. 13a: u = 13

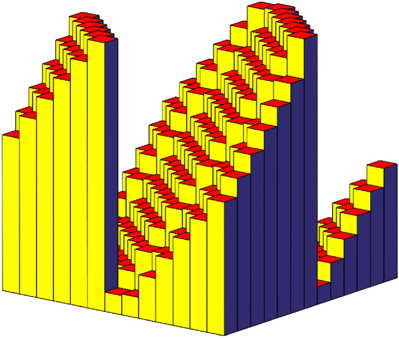
Abb. 13b: Histogramm

7 Eigenschaften

7.1 Arithmetische Folgen

Die Null befindet sich immer in der linken Spalte in der Mitte. Die zugehörige Zeile besteht aus einer arithmetischen Folge mit dem Zuwachs u + 1.

Die mittlere Spalte besteht in der Richtung von unten nach oben aus einer arithmetischen Folge mit dem Zuwachs u – 1.

7.2 Zahl in der Mitte

Die Zahl in der Mitte ist . Die Zeilen-, Spalten- und Diagonalensumme ist das u-fache davon.

7.3 Ergänzungssymmetrie

Zwei Zahlen, die punktsymmetrisch bezüglich der Zahl in der Mitte liegen, ergänzen sich auf das Doppelte der Zahl in der Mitte.

Wir können diese Symmetrie sichtbar machen, indem wir sämtliche Zahlen um die Zahl in der Mitte absenken. Die Zeilen-, Spalten- und Diagonalensummen werden dann null.

Im Folgenden die entsprechenden Beispiele. Die Histogramme gehen jetzt auch nach unten.

1	2	–3
–4	0	4
3	–2	–1

Abb. 14a: u = 3. Symmetrische Version

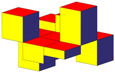
Abb. 14b: Histogramm

1	7	8	–11	–5
–3	–2	4	10	–9
–12	–6	0	6	12
9	–10	–4	2	3
5	11	–8	–7	–1

Abb. 15a: u = 5. Symmetrische Version

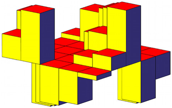
Abb. 15b: Histogramm

1	9	17	18	–23	–15	–7
–5	3	4	12	20	–21	–13
–11	–10	–2	6	14	22	–19
–24	–16	–8	0	8	16	24
19	–22	–14	–6	2	10	11
13	21	–20	–12	–4	–3	5
7	15	23	–18	–17	–9	–1

Abb. 16a: u = 7. Symmetrische Version

Abb. 16b: Histogramm

1	11	21	31	32	–39	–29	–19	–9
–7	3	13	14	24	34	–37	–27	–17
–15	–5	–4	6	16	26	36	–35	–25
–23	–22	–12	–2	8	18	28	38	–33
–40	–30	–20	–10	0	10	20	30	40
33	–38	–28	–18	–8	2	12	22	23
25	35	–36	–26	–16	–6	4	5	15
17	27	37	–34	–24	–14	–13	–3	7
9	19	29	39	–32	–31	–21	–11	–1

Abb. 17a: u = 9. Symmetrische Version

Abb. 17b: Histogramm

1	13	25	37	49	50	–59	–47	–35	–23	–11
–9	3	15	27	28	40	52	–57	–45	–33	–21
–19	–7	5	6	18	30	42	54	–55	–43	–31
–29	–17	–16	–4	8	20	32	44	56	–53	–41
–39	–38	–26	–14	–2	10	22	34	46	58	–51
–60	–48	–36	–24	–12	0	12	24	36	48	60
51	–58	–46	–34	–22	–10	2	14	26	38	39
41	53	–56	–44	–32	–20	–8	4	16	17	29
31	43	55	–54	–42	–30	–18	–6	–5	7	19
21	33	45	57	–52	–40	–28	–27	–15	–3	9
11	23	35	47	59	–50	–49	–37	–25	–13	–1

Abb. 18a: u = 11. Symmetrische Version

Abb. 18b: Histogramm

1	15	29	43	57	71	72	–83	–69	–55	–41	–27	–13
–11	3	17	31	45	46	60	74	–81	–67	–53	–39	–25
–23	–9	5	19	20	34	48	62	76	–79	–65	–51	–37
–35	–21	–7	–6	8	22	36	50	64	78	–77	–63	–49
–47	–33	–32	–18	–4	10	24	38	52	66	80	–75	–61
–59	–58	–44	–30	–16	–2	12	26	40	54	68	82	–73
–84	–70	–56	–42	–28	–14	0	14	28	42	56	70	84
73	–82	–68	–54	–40	–26	–12	2	16	30	44	58	59
61	75	–80	–66	–52	–38	–24	–10	4	18	32	33	47
49	63	77	–78	–64	–50	–36	–22	–8	6	7	21	35
37	51	65	79	–76	–62	–48	–34	–20	–19	–5	9	23
25	39	53	67	81	–74	–60	–46	–45	–31	–17	–3	11
13	27	41	55	69	83	–72	–71	–57	–43	–29	–15	–1

Abb. 19a: u = 13. Symmetrische Version

Abb. 19b: Histogramm

Die symmetrischen Quadrate haben links oben eine 1, links unten die Seitenlänge u.

Literatur

Euler, Leonhard (1782) : E 530, Recherches sur une nouvelle espèce de quarrés magiques, Vlissingen 1782 - Opera I 7, p. 291-392.