Hans Walser, [20150624]
Lucas-Zahlen
1 Worum geht es?
Visualisierungen der Lucas-Zahlen
2 Was sind die Lucas-Zahlen?
Die Zahlen der Folge 1, 3, 4, 7, 11, 18, 29, ... hei§en Lucas-Zahlen.
Bezeichnung:
![]()
Rekursive Darstellung:
Startwerte
![]() , Rekursion:
, Rekursion:
![]()
Es handelt sich also um die bekannte Fibonacci-Rekursion.
Explizite Darstellung:
![]()
Dabei ist
![]() (goldener
Schnitt, vgl. (Walser 2013)).
(goldener
Schnitt, vgl. (Walser 2013)).
Grenzwert des Quotienten aufeinanderfolgender Lucas-Zahlen:
![]()
Die Lucas-Zahlen haben also sehr viel mit den Fibonacci-Zahlen gemeinsam. Vgl. (Walser 2012). Daher werden sich auch die Visualisierungen an jene der Fiboancci-Zahlen anlehnen.
Person: FranŤois Edouard Anatole Lucas (1842-1891).
3 Darstellung mit Quadraten
Die Abbildung 1 zeigt zwei verschiedene Anordnungen der Fibonacci-Quadrate.
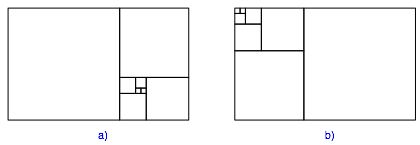
Abb. 1: Fibonacci-Quadrate
Die SeitenlŠngen der Quadrate sind die Fibonacci-Zahlen 1, 1,2, 3, 5, 8, 13, 21, ... . Die Anordnung der Abbildung 1a) ist spiralfšrmig. Bei der Anordnung der Abbildung 1b) wird von links oben nach rechts unten gearbeitet.
Beide Anordnungen lassen sich auf Lucas-Zahlen źbertragen. Wir haben aber eine Startlźcke (Abb. 2 und 3).

Abb. 2: Lucas-Zahlen-Spirale mit Startlźcke

Abb. 3: Lucas-Zahlen mit Startlźcke
4 Trapeze und Rhomben
Die Abbildung 4 zeigt eine Visualisierung der Lucas-Zahlen mit Trapezen und Rhomben. Die Figuren haben Winkel von 60ˇ und 120ˇ.
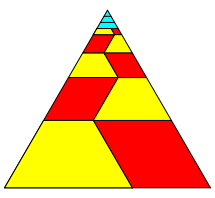
Abb. 4: Trapeze und Rhomben
Die SeitenlŠngen der Rhomben sind die Lucas-Zahlen. Die SeitenlŠngen der Trapeze sind jeweils drei aufeinanderfolgende Lucas-Zahlen.
Durch Einbetten der Figur in ein gleichseitiges Dreieck lesen wir folgende Beziehung ab:
![]()
Der Korrekturterm 3 ergibt sich durch die hellblaue Spitze des Dreieckes.
Fźr das Fibonacci-Analogon siehe (Plaza and Walser 2013).
5 Rhomben allein
Wir denken uns je zwei Rhomben am gemeinsamen Eckpunkt gelenkig verbunden.
Wir kšnnen sie dann zusammenklappen zur Figur der Abbildung 5. Der Klappwinkel ist jeweils 60ˇ. Die Endfigur ist ein affines Bild der Figur der Abbildung 3.

Abb. 5: Zusammenklappen der Rhomben um 60ˇ
Wenn wir um den 120ˇ-Winkel zusammenklappen, ergibt sich die Situation der Abbildung 6.

Abb. 6: Zusammenklappen der Rhomben um 120ˇ
6 Trapeze allein
Nun klappen wir die Trapeze um 60ˇ zusammen (Abbildung 7).
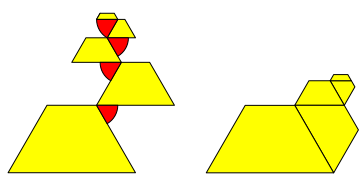
Abb. 7: Zusammenklappen der Trapeze um 60ˇ
Aus sechs Teilen kšnnen wir einen Stern zusammensetzen (Abbildung 8).
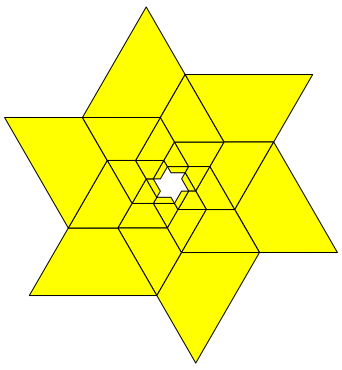
Abb. 8: Lucas-Stern
Nun klappen wir die Trapeze um 120ˇ zusammen (Abbildung 9).
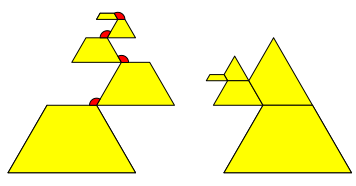
Abb. 9: Zusammenklappen der Trapeze um 120ˇ
Auch daraus lŠsst sich mit 6 Teilen ein Stern bauen (Abb. 10). Er ist spiegelbildlich zum Stern der Abbildung 8.
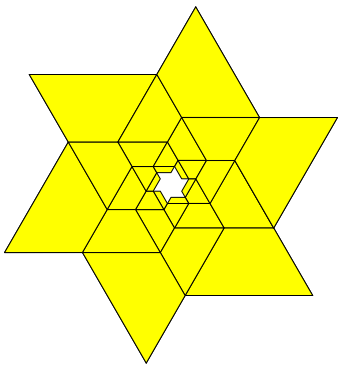
Abb. 10: Stern
Literatur
Plaza, Angel and Walser, Hans (2013): Proof Without Words: Fibonacci Triangles and Trapezoids. Mathematics Magazine. 86 (2013) p. 55.
Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-60-8.
Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing źber populŠrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.