Hans Walser, [20170811]
LŠmpel-WŸrfel
Indirekte Anregung: H. Sch., W.
1 Definition
In einem rŠumlichen kartesischen Koordinatensystem ist ein LŠmpel-WŸrfel ein WŸrfel mit ganzzahligen Eckpunktkoordinaten und ganzzahligen KantenlŠngen (L. LŠmpel, 1865).
2 Beispiele
2.1 Beispiel 1
Die Abbildung 1 zeigt den durch die drei Vektoren
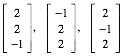(1)
aufgespannten WŸrfel. Die drei Vektoren sind paarweise orthogonal und haben je die LŠnge 3. Wir erhalten also einen LŠmpel-WŸrfel.
Der zweite und der dritte Vektor entstehen aus dem ersten durch zyklische Vertauschung.
Die Zahlen 2, 2, 1, 3 bilden ein pythagoreisches Quadrupel.
Abb. 1: LŠmpel-WŸrfel
Die Abbildung 2 zeigt die drei Risse in klassischer Manier.
Die zyklische Vertauschung zeigt sich in der Kongruenz der drei Risse.
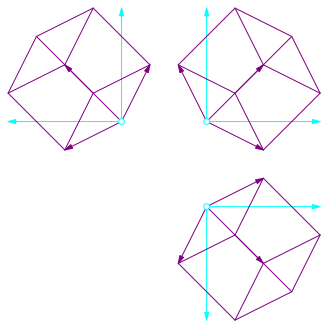
Abb. 2: Grund-, Auf- und Seitenriss
2.2 Beispiel 2
Die drei Vektoren
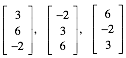(2)
sind paarweise orthogonal und haben die LŠnge 7. Sie spannen also ebenfalls einen LŠmpel-WŸrfel auf.
3 Allgemein
Die drei Vektoren
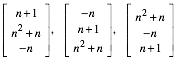(3)
sind
paarweise orthogonal und haben die LŠnge 
. Sie spannen daher einen LŠmpel-WŸrfel auf.
Der Nachweis der OrthogonalitŠt erfolgt mit dem Skalarprodukt, die Berechnung der LŠnge mit Pythagoras.
Beispiele:
FŸr n = 0 ergibt sich der EinheitswŸrfel des kartesischen Koordinatensystems.
FŸr n = 1 erhalten wir das Beispiel (1) (Abb. 1 und 2).
FŸr n = 2 erhalten wir das Beispiel (2).
Offene
Frage: Erhalten wir mit 
und den
Formeln (3) alle LŠmpel-WŸrfel?
4 Pythagoreische Quadrupel
Die vier Zahlen
(4)
bilden ein pythagoreisches Quadrupel. Es ist:
(5)
Frage:
Erhalten wir mit 
und den
Formeln (5) alle pythagoreischen
Quadrupel?