Hans Walser, [20140224]

Konvergente Fibonacci-Folgen

1 Worum geht es?

Die klassische Fibonacci-Folge 1, 1, 2, 3, 5, 8, 13, 21, ... ist divergent.

Wir untersuchen Beispiele von konvergenten Folgen mit der Rekursion:

Jedes Folgenglied ist also eine Linearkombination der beiden vorangehenden Folgenglieder (Walser 2012, S.15).

Der Grenzwert der Folge soll aber von null verschieden sein.

2 Beispiel

2.1 Arithmetisches Mittel

Wir arbeiten mit der Rekursion:

Jedes Folgenglied ist das arithmetische Mittel der beiden vorangehenden Folgenglieder.

Die Tabelle 1 zeigt Beispiele x_n und y_n mit zwei verschiedenen Startwertpaaren.

n	xn	yn
0	1	0
1	0	1
2	0.5	0.5
3	0.25	0.75
4	0.375	0.625
5	0.3125	0.6875
6	0.34375	0.65625
7	0.32812	0.67188
8	0.33594	0.66406
9	0.33203	0.66797
10	0.33398	0.66602

Tab.1: Zwei Beispiele

2.2 Visualisierungen

Wir fassen x_n und y_n als Koordinaten eines Punktes A_n(x_n,y_n) auf. Wir erhalten eine Punktfolge, in welcher jeder Punkt Mittelpunkt der beiden vorangehenden Folgenpunkte ist (Abb. 1).

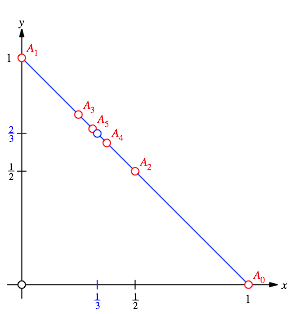
Abb. 1: Punktfolge

Die Punktfolge hat einen Grenzpunkt (Häufungspunkt) .

Die Abbildung 2 zeigt eine andere Visualisierung.

Abb. 2: Visualisierung

2.3 Beweis

Die Tabelle 1 lässt vermuten:

Für den Beweis für die Folge x_n arbeiten wir mit Brüchen relativ zum vermuteten Grenzwert (Tab. 2).

Tab. 2: Darstellung in Brüchen

Es drängt sich die Vermutung für die explizite Formel auf:

Dies kann induktiv bewiesen werden. Für die Startwerte ist die Formel ok. Einsetzen in die Rekursionsformel ergibt:

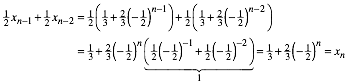
Aus der expliziten Formel folgt der vermutete Grenzwert .

Für die Folge y_n gilt entsprechend:

Für die Folge a_n ergibt sich für die Startwerte a₀ und a₁ wegen der Linearität die Folge:

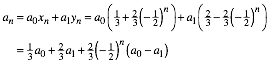
Weiter ist dann:

Das heißt aber, dass wir mit geeigneter Wahl der Startwerte a₀ und a₁ jeden beliebigen Grenzwert erreichen können.

Die triviale Lösung besteht darin, die beiden Startwerte gleich dem anvisierten Grenzwert zu setzen. Wir erhalten dann eine konstante Folge.

Wir können einen der beiden Startwerte normieren. Beispiel: Für den Grenzwert π haben wir die Bedingung:

Mit der Normierung a₀ = 0 ergibt sich . Die Tabelle 3 zeigt die numerischen Werte.

n	an
0	0.00000
1	4.71239
2	2.35619
3	3.53429
4	2.94524
5	3.23977
6	3.09251
7	3.16614
8	3.12932
9	3.14773
10	3.13852
11	3.14313
12	3.14083
13	3.14198
14	3.14140
15	3.14169

Tab. 3: Grenzwert π

2.4 Matrizen

Die Rekursion

kann auch in Matrizenform geschrieben werden:

Damit wird explizit:

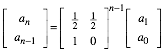
Die Tabelle 4 gibt einige Potenzen der Matrix :

Tab. 4: Potenzen der Matrix

Es ist:

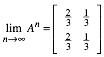
Die Grenzmatrix ist singulär.

3 Allgemein

3.1 Formel von Binet

Für eine Folge mit der Rekursion und den Startwerten a₀ und a₁ gilt die explizite Formel (Formel von Binet):

Dabei sind die Lösungen der quadratischen Gleichung (man beachte die abweichende Schreibweise zu der in der Schule üblichen „p-q-Formel“)

also:

Die Folge a_n ist also eine Linearkombination von zwei geometrischen Folgen mit den Quotienten und (Walser 2012, S.15, 16).

3.2 Sonderfall

Im Sonderfall p + q = 1 ist jedes Folgenglied ein gewichtetes Mittel der beiden vorangehenden Folgenglieder.

In diesem Fall ist q = 1 – p und damit:

Daher wird:

Damit erhalten wir für die Formel von Binet:

Für erhalten wir den Grenzwert:

Somit haben wir drei freie Parameter, um einen anvisierten Grenzwert zu erhalten.

Wir kontrollieren die Grenzwertformel an unserem schon bekannten Beispiel der Folge x_n. Es ist , x₀ = 1, x₁ = 0 und damit:

3.3 Der Goldene Schnitt

Ein interessantes Beispiel ist folgendes. Wir arbeiten mit dem Goldenen Schnitt (Walser, 2013).

Rekursion:

Die Tabelle 5 gibt die numerischen Werte für zwei Startwertpaare.

n
0	1	0
1	0	1
2	0.61803	0.38197
3	0.23607	0.76393
4	0.47214	0.52786
5	0.32624	0.67376
6	0.41641	0.58359
7	0.36068	0.63932
8	0.39512	0.60488
9	0.37384	0.62616
10	0.38699	0.61301

Tab. 5: Goldener Schnitt

Es ist:

Die Abbildung 3 illustriert die Lage der Punkte A_n(x_n,y_n).

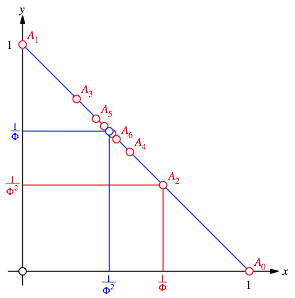
Abb. 3: Goldener Schnitt

Der Punkt A₂ unterteilt die Strecke A₀A₁im Verhältnis Minor-Mayor, der Grenzpunkt unterteilt dieselbe Strecke im umgekehrten Verhältnis. Wer Lust hat, kann ein Pentagramm einpassen (Abb. 4).

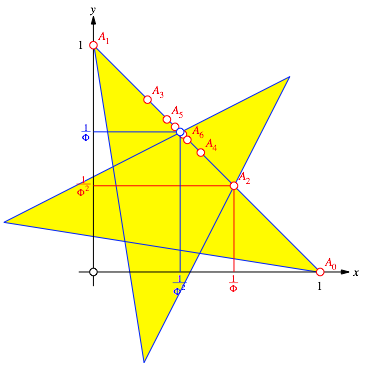
Abb. 4: Pentagramm

Die Abbildung 5 zeigt das Analogon zur Abbildung 2.

Abb. 5: Die Goldene Fresse

3.4 Die Matrix

Die Rekursion kann wie folgt beschrieben werden:

Die Rekursionsmatrix hat die oben beschriebenen Eigenwerte:

Im Sonderfall p + q = 1 sind die beiden Zeilensummen 1. Bei nicht negativen Einträgen p und q handelt es sich um eine so genannte Übergangsmatrix (auch stochastische Matrix oder Prozessmatrix genannt).

4 Alternierende Rekursion

4.1 Die Rekursion

Wir verwenden zwei Zahlen p und q mit p + q = 1 und verfahren wie folgt.

4.2 Beispiel

Für erhalten wir:

n	xn	yn
0	1	0
1	0	1
2	0.66666667	0.33333333
3	0.44444444	0.55555556
4	0.59259259	0.40740741
5	0.54320988	0.45679012
6	0.57613169	0.42386831
7	0.56515775	0.43484225
8	0.57247371	0.42752629
9	0.57003506	0.42996494
10	0.57166082	0.42833918
11	0.5711189	0.4288811
12	0.57148018	0.42851982
13	0.57135976	0.42864024
14	0.57144004	0.42855996
15	0.57141328	0.42858672
16	0.57143112	0.42856888
17	0.57142517	0.42857483
18	0.57142914	0.42857086
19	0.57142782	0.42857218
20	0.5714287	0.4285713

Tab. 6: Beispiel

Wir vermuten:

Die Abbildung 6 illustriert den Sachverhalt.

Abb. 6: Grenzpunkt

Für beliebige Startwerte a₀ und a₁ erhalten wir den Grenzwert:

4.3 Allgemein

Für ein beliebiges p und damit q = 1 – p erhalten wir für die Startwerte

n	xn	yn	an
0	1	0	a0
1	0	1	a1

die Grenzwerte:

sowie:

Beweis?

4.4 Nochmals der Goldene Schnitt

Wir wählen wiederum . Damit erhalten wir die Tabelle 7.

n	xn	yn
0	1	0
1	0	1
2	0.61803399	0.38196601
3	0.38196601	0.61803399
4	0.52786404	0.47213596
5	0.47213595	0.52786405
6	0.50657781	0.49342219
7	0.49342219	0.50657781
8	0.50155281	0.49844719
9	0.49844719	0.50155281
10	0.50036657	0.49963343

Tab. 7: Goldener Schnitt

Interessant ist die jeweilige Vertauschung bei aufeinanderfolgenden Paaren.

Es ist

Wir haben einen Drang zur Mitte (Abb. 7).

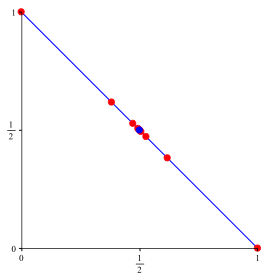
Abb. 7: Goldener Schnitt und Symmetrie

Die Abbildung 8 zeigt die zugenhörige Flächendarstellung.

Abb. 8: Symmetrischer Goldener Schnitt

Literatur

Walser, Hans (2012): Fibonacci. Zahlen und Figuren. Leipzig, EAGLE, Edition am Gutenbergplatz 2012. ISBN 978-3-937219-60-8.

Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.