Hans Walser, [20231218]
Kugelvolumen
1 Worum es geht
Visualisierung einer Idee von Archimedes zur Berechnung des Kugelvolumens
2 Die Idee von Archimedes
Zur Berechnung des Kugelvolumens macht Archimedes einen Vergleich zwischen der Kugel einerseits und andererseits einem Zylinder mit gleichem Radius und dem Kugeldurchmesser als Höhe, bei dem von beiden Seiten her ein Kegel mit dem Öffnungswinkel 90° eingebohrt wurde (Abb. 1). Dabei werden die Volumenberechnungen für Zylinder und Kegel als bekannt vorausgesetzt.
Für die folgenden Figuren sei der Kugelradius 1. Dies ist keine Einschränkung der Allgemeinheit. Bei einem beliebigen Radius r müssen wir beim Volumen einfach mit r3 multiplizieren.
Für diese Daten ist das Zylindervolumen 2π, das Kegelvolumen (Doppelkegel) 2π/3. Für das Volumen des angebohrten Zylinders ergibt sich also 4π/3.
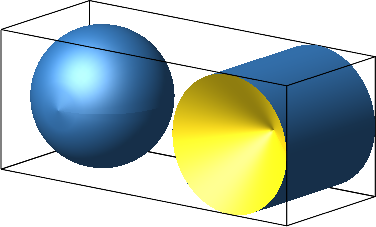
Abb. 1: Vergleich
Nun schneiden wir bei beiden Figuren senkrecht zur Achse im gleichen Abstand x vom Mittelpunkt (Abb. 2).
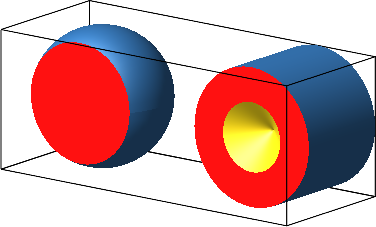
Abb. 2: Gleiche Schnittflächen
Bei der Kugel gibt das einen Schnittkreis mit dem Radius √(1 – x2), beim angebohrten Zylinder einen Kreisring mit dem Außenradius 1 und dem Innenradius x. Beide Schnittfiguren haben den Flächeninhalt (1 – x2)π, sind also flächengleich.
Nach dem Prinzip von Cavalieri haben daher die Kugel und der angebohrte Zylinder dasselbe Volumen, also 4π/3. Dies war die Idee von Archimedes.
Die Abbildung 3 zeigt die Schnittflächen bei Variation von x.

Abb. 3: Variation der Schnitte
3 Transformation
Die Idee ist nun, die Kugel zum angebohrten Zylinder zu transformieren (Abb. 4), und zwar so, dass die Schnittflächen während der Transformation invariant bleiben (Abb. 5). Damit bleibt auch das Volumen während des Transformationsprozesses invariant.
Die Außenfläche der Kugel wird fässchenförmig, bevor sie zum Zylinder wird.

Abb. 4: Transformation
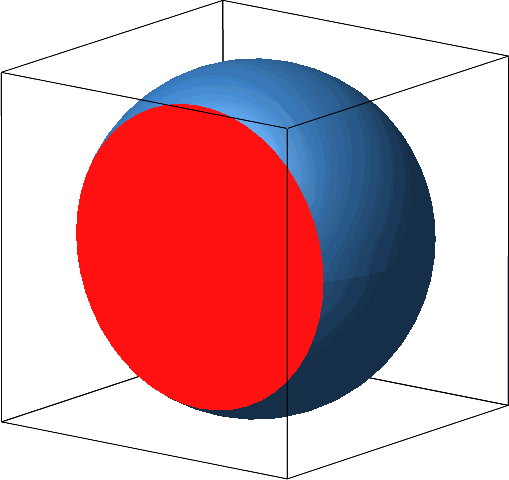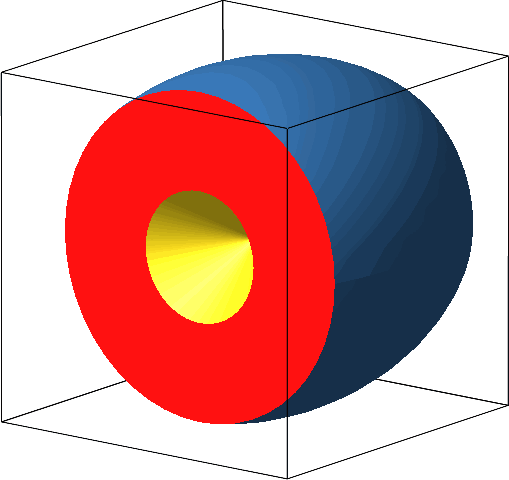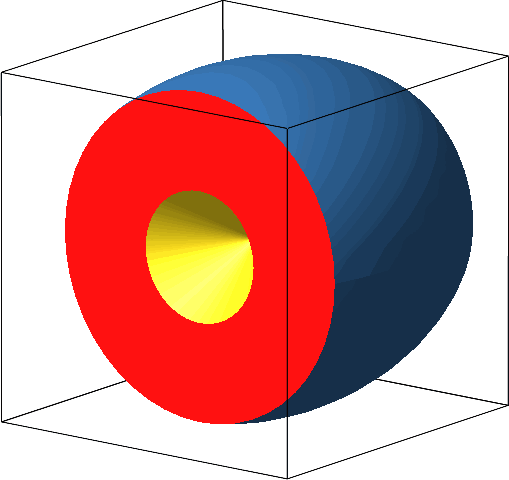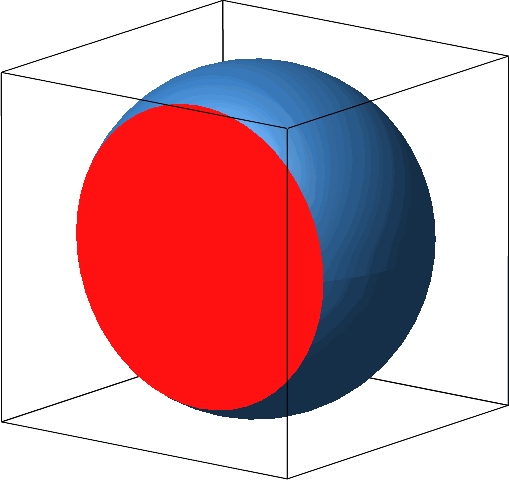
Abb. 5: Invariante Schnittfläche
Die Abbildung 6 zeigt einen Achsenschnitt.

Abb. 6: Achsenschnitt
Die Profilkurve des Fässchens liegt auf einer Ellipse (Abb. 7).
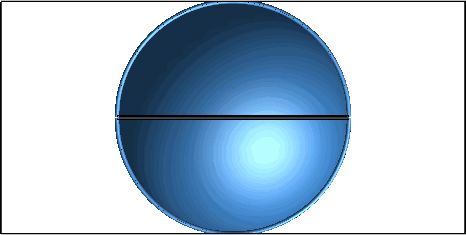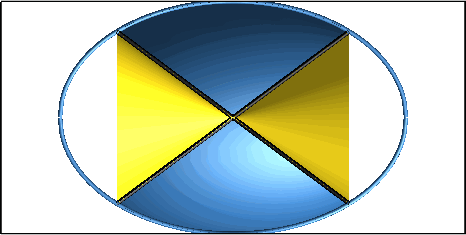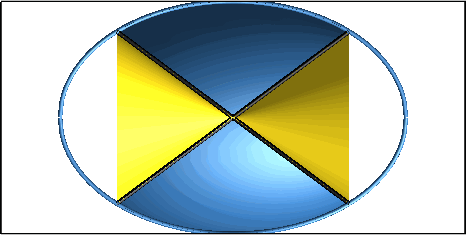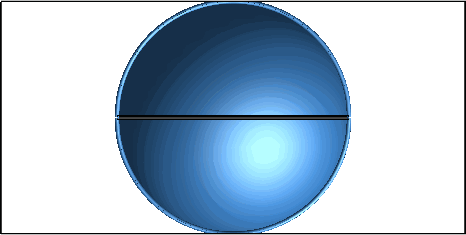
Abb. 7: Ellipsenbogen als Profilkurve
Weblinks
Hans Walser: Kreisring
https://walser-h-m.ch/hans/Miniaturen/K/Kreisring/Kreisring.html