Hans Walser, [20170528]

Kreise im DIN Rechteck

Wir beginnen mit einem Rechteck im DIN-Format (Abb. 1a). Für allfällige Rechnungen setzen wir die Länge auf und die Breite auf 2.

Wir zeichnen über jeder Rechteckseite den Thaleskreis (Abb. 1b). Die Thaleskreise haben die Radien und 1.

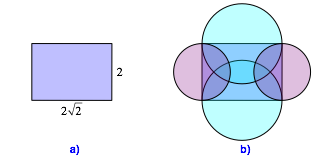
Abb. 1: DIN-Rechteck und Thaleskreise

Die Figur hat einen Inkreis und einen Umkreis (Abb. 2).

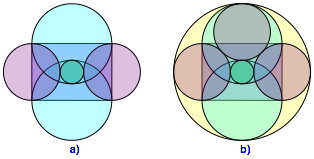
Abb. 2: Inkreis und Umkreis

Der Inkreisradius ist die halbe Differenz der beiden Seitenlängen (gilt in jedem Rechteck), in unserem Fall . Der Umkreisradius ist die halbe Summe der beiden Seitenlängen (gilt in jedem Rechteck), in unserem Fall . Das Produkt der beiden Radien ist 1, sie sind also Kehrwerte voneinander.

In die Eckenspickel können wir kleine Kreise einpassen (Abb. 3a). Der Radius dieser Kreise ist (Abb. 3b). Beweis durch Nachrechnen.

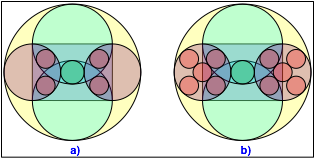
Abb. 3: Kreise in den Spickeln

Oben und unten können wir Kreise mit dem Radius 1 einpassen (Abb. 4). Sie sind also gleich groß wie die Thaleskreise über den kurzen Seiten des DIN-Rechtecks.

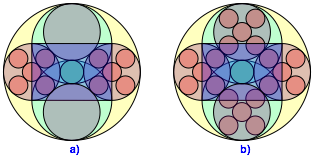
Abb. 4: Ergänzung

Nun können wir außen Kopien des Inkreises einpassen (Abb. 5a). Ihre Mittelpunkte liegen auf gleicher Achse wie die Mittelpunkte der Thaleskreise über den kurzen Seiten. Beweise durch Nachrechnen.

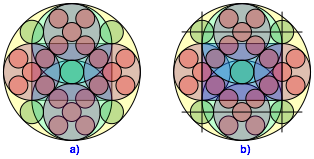
Abb. 5: Einpassen von Inkreiskopien