1 Worum geht es?

Zwei Kegelschnitte nenne ich konjugiert, wenn die Brennpunkte des einen auf dem anderen liegen und umgekehrt.

Es werden einige Beispiele vorgestellt und einige Eigenschaften festgestellt. Verifikation jeweils mit DGS.

2 Konjugierte Ellipsen

Wir beginnen mit einem beliebigen Parallelogramm. Dazu zeichnen wir eine Ellipse, welche zwei diametrale Ecken des Parallelogramms als Brennpunkte hat und durch die beiden anderen Ecken verläuft (rot in Abb. 1a).

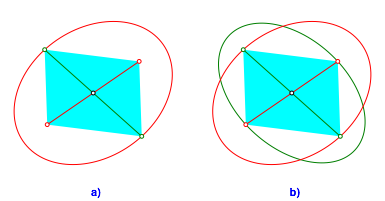
Abb. 1: Konjugierte Ellipsen

Nun zeichnen wir eine zweite Ellipse (grün in Abb. 1b) mit vertauschten Rollen der vier Parallelogrammecken.

Die beiden Ellipsen sind in unserem Sinn konjugiert.

3 Dritte konjugierte Ellipse

Die Abbildung 2a zeigt eine dritte Ellipse (blau), die je zu den beiden anderen konjugiert ist. Wir haben also drei paarweise konjugierte Ellipsen.

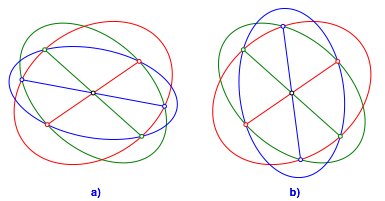
Abb. 2: Dritte konjugierte Ellipse

Die Abbildung 2b zeigt eine andere Lösung für eine dritte konjugierte Ellipse. Die beiden Lösungen sind aber nicht zueinander konjugiert.

Liegt das an der fehlenden Symmetrie?

4 Symmetrische Lösungen

Die Abbildung 3a zeigt eine symmetrische Lösung von drei paarweise konjugierten Ellipsen so dass einem das Herz im Leibe lacht. Welches Achsenverhältnis haben die Ellipsen?

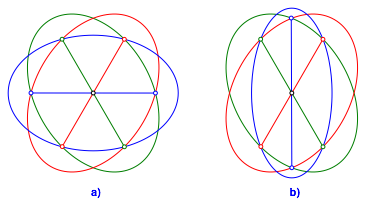
Abb. 3: Symmetrische Lösungen

Allerdings gibt es auch da eine weniger symmetrische dritte Ellipse (Abb. 3b).

In der Abbildung 4a ist grün mit rot konjugiert, weiter rot mit blau und blau mit violett und violett mit grün. Wir haben eine geschlossene Kette von aufeinanderfolgenden konjugierten Ellipsen. Hingegen ist grün nicht mit blau konjugiert und rot nicht mit violett. Wir haben also keine paarweise Konjugation.

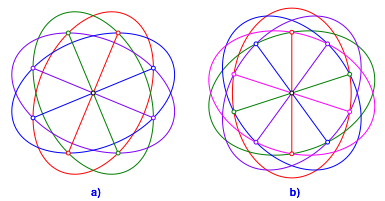
Abb. 4: Symmetrische Ketten von konjugierten Ellipsen

Wie steht es mit den Ellipsen der Abbildung 4b?

Wir vermuten: Es gibt höchstens drei paarweise konjugierte Ellipsen. Beweis?

Wir haben einen analogen Sachverhalt in der elementaren Geometrie: Es gibt höchstens drei Punkte mit paarweise gleichem Abstand.

5 Umkreis und interessante Ellipsen

Kehren wir zum asymmetrischen Beispiel der Abbildung 2a zurück. Wir vermuten schon lange, dass die Figur einen Umkreis hat (Abb. 5a). Die konjugierten Ellipsen haben alle dieselbe lange Achse. Verifikation mit DGS.

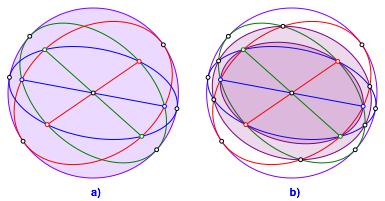
Abb. 5: Umkreis und weitere Ellipsen

Das Sechseck der sechs Brennpunkte hat eine Umellipse (Abb. 5b). Das ist trivial, da jedes punktsymmetrische Sechseck als affin reguläres Sechseck eine Umellipse hat.

In der Abbildung 5b haben wir aber noch sechs weitere Schnittpunkte, welche auf einer Ellipse liegen. Dies ist nicht trivial, da eine Ellipse schon durch fünf Punkte festgelegt ist. Verifikation mit DGS.

6 Geschlossene Ketten von konjugierten Ellipsen

Wir können eine beliebig lange geschlossene Kette von aufeinanderfolgend konjugierten Ellipsen zeichnen.

Wir beginnen mit einer beliebigen Ellipse (rot in Abb. 6a) und wählen auf ihr zwei diametrale Punkte. Diese verwenden wir als Brennpunkte für die zweite Ellipse (grün in Abb. 6b), welche auch noch durch die Brennpunkte der ersten Ellipse verlaufen soll.

Abb. 6: Start und erster Schritt

Nun wählen wir zwei diametrale Schnittpunkte (wir haben eine dichotomische Wahl) der beiden Ellipsen (blau in Abb. 7a) als Brennpunkte der nächsten Ellipse, welche durch die Brennpunkte der ersten Ellipse laufen soll. Sie verläuft dann automatisch auch durch die Brennpunkte der zweiten Ellipse.

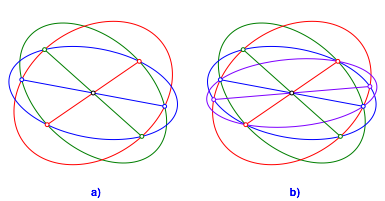
Abb. 7: Zweiter und dritter Schritt

Wir wählen nun diejenigen Schnittpunkte der neuen Ellipse mit der ersten Ellipse, welche nicht Brennpunkte er vorhergehenden Ellipse waren, als Brennpunkte der folgenden Ellipse. Diese soll durch die Brennpunkte der ersten Ellipse gehen. Sie geht dann automatisch auch durch die Brennpunkte der unmittelbar vorhergehenden Ellipse.

Allgemein: es sei e₁ die erste Ellipse, und die Ellipsen bis e_n seien gezeichnet. Von den vier Schnittpunkten von e_n mit e₁ wählen wir diejenigen beiden, welche nicht schon Brennpunkte von e_n_–1 waren, als Brennpunkte von e_n₊₁. Die Ellipse e_n₊₁ soll durch die Brennpunkte von e₁ verlaufen. Sie verläuft dann automatisch auch durch die Brennpunkte von e_n.

Zwei aufeinanderfolgende Ellipsen und die Ellipse e₁ sind dann paarweise konjugiert, aber die mittelbar aufeinanderfolgenden Ellipsen e_n_–1 und e_n₊₁ sind nicht konjugiert.

Wir können also jederzeit abbrechen und haben eine geschlossene Kette von aufeinanderfolgend konjugierten Ellipsen. Zudem sind alle Ellipsen mit e₁ konjugiert.

Die Abbildung 8 zeigt die beiden folgenden Schritte.

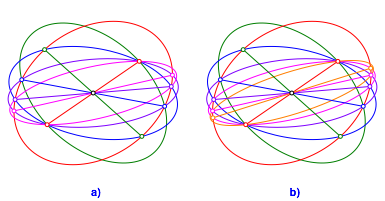
Abb. 8: Folgende Schritte

Die Ellipsen werden immer schmaler und häufen sich gegen die lange Achse von e₁.

7 Hyperbeln

Mit Hyperbeln geht es analog. Die Abbildung 9 zeigt drei paarweise konjugierte Hyperbeln. Statt einem Umkreis haben wir nun einen Inrkreis.

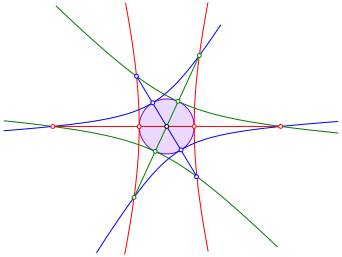
Abb. 9: Paarweise konjugierte Hyperbeln

8 Kombination

In der Abbildung 10 sind abwechslungsweise Ellipsen und Hyperbeln konjugiert. Die beiden Ellipsen sind aber nicht konjugiert, auch die beiden Hyperbeln sind nicht konjugiert.

Wir haben weder Umkreis noch Inkreis.

Es ist mir nicht gelungen, ein Tripel aus zwei Ellipsen und einer Hyperbel paarweise zu konjugieren. Offenbar haben wir da so etwas wie ein Paritätsproblem.

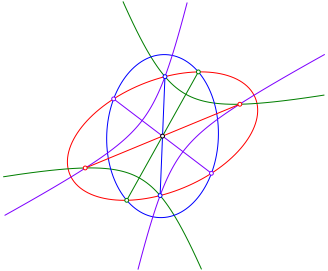
Abb. 10: Ellipsen und Hyperbeln