Hans Walser, [20140925]

Konforme Punktgitter

1 Worum geht es?

Es werden Punktgitter, welche kleine „Quadrate“ darstellen, mit Hilfe differenzierbarer komplexer Funktionen dargestellt. Dabei wir die Software GeoGebra verwendet.

2 Beispiele

Die Eingabezeile für die Beispiele ist jeweils:

Folge[Folge[f(a + i*b), a, amin, amax, astep], b, bmin, bmax, bstep]

Dabei ist:

f die verwendete Funktion

amin, amax, bmin, bmax die linke, rechte, untere, obere Begrenzung des Definitionsbereiches

astep und bstep die Schrittlängen (Maschenbreiten) im Definitionsbereich. Für „quadratische“ Gitter muss astep = bstep sein. Bei periodischen Funktionen muss step ein Bruchteil der Periodenlänge sein.

2.1 Kartesisches Gitter

Identität: f(a + i*b) = a + i*b

Folge[Folge[a + i*b, a, 0, 5, 1], b, 0, 8, 1]

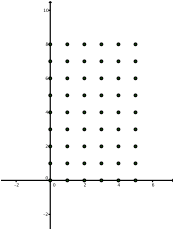
Abb. 1: Kartesisches Gitter

2.2 Gedrehtes kartesisches Gitter

Mit dem Faktor exp(i*α) kann um den Ursprung um den Winkel α gedreht werden.

Folge[Folge[exp(i*π/12)*(a + i*b), a, 0, 5, 1], b, 0, 8, 1]

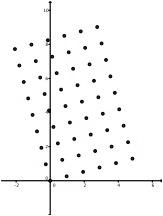
Abb. 2: Drehung

2.3 Kreise und Geraden

Die Exponentialfunktion liefert das klassische Netz von konzentrischen Kreisen und radialen Geraden.

Folge[Folge[exp(a + i*b), a, -5, 5, π/12], b, 0, 2*π, π/12]

Abb. 3: Kreise und Geraden

2.4 Parabeln

Die Quadratfunktion liefert konfokale Parabeln.

Folge[Folge[(a + i*b)^2, a, 0, 8, 1], b, -8, 8, 1]

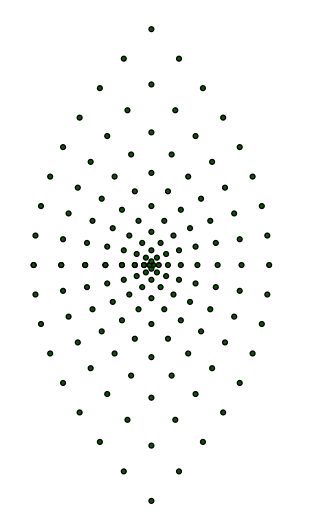
Abb. 4: Parabeln

2.5 Ellipsen und Hyperbeln

Die hyperbolische Kosinusfunktion liefert konfokale Ellipsen und Hyperbeln

Folge[Folge[cosh(a + i*b), a, 0, π, π/12], b, 0, π, π/12]

Leider funktioniert das in GeoGebra nicht. Die Kreisfunktionen und die hyperbolischen Funktionen sind offenbar in GeoGebra nur reell implementiert. Wir müssen daher von Hand arbeiten.

Wegen cosh(z) = (exp(z) + exp(-z))/2 kommen wir mit der Exponentialfunktion durch.

Folge[Folge[(exp(a + i*b) + exp(-(a + i*b)))/2, a, 0, π/2, π/12], b, -π, π, π/12]

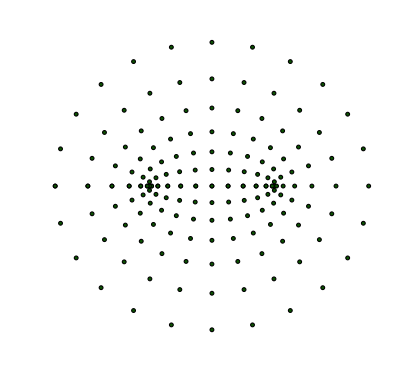
Abb. 5: Ellipsen und Hyperbeln

2.6 Gleichseitige Hyperbeln. Sattel

Wir arbeiten mit der Wurzelfunktion. Mit

Folge[Folge[sqrt(a + ί b), a, -8, 8, 1], b, -8, 8, 1]

erhalten wir allerdings nur die halbe Miete.

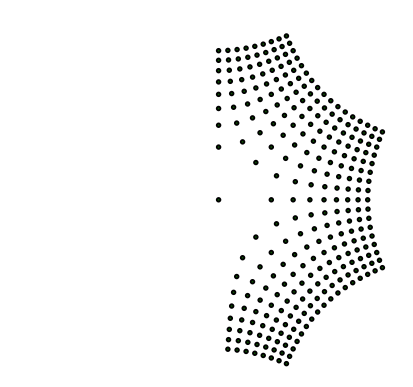
Abb. 6a: Nur die Hälfte

Das liegt daran, dass die Umkehrfunktion der nicht bijektiven Quadratfunktion nur auf einer Hälfte funktioniert.

Wir müssen die andere Hälfte von Hand nachfügen, indem wir eine zweite Folge angeben.

Folge[Folge[sqrt(a + ί b), a, -8, 8, 1], b, -8, 8, 1]

Folge[Folge[-sqrt(a + ί b), a, -8, 8, 1], b, -8, 8, 1]

Das Minuszeichen vor der Wurzel spiegelt am Ursprung.

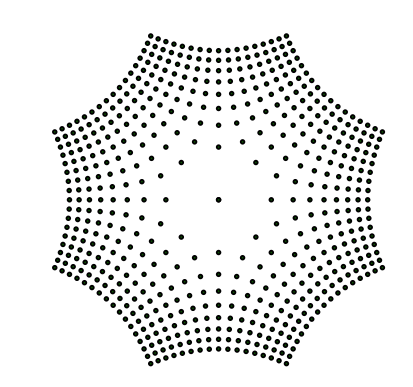
Abb. 6b: Beide Hälften

Werden die Hyperbeln der einen Schar als Niveaulinien interpretiert, haben wir einen Sattel- oder Passpunkt.

2.7 Affensattel

Eingaben:

A = 0 + 0*i

Folge[Folge[Folge[exp(i*2*k* π/3) (a + i*b)^(1/3), a, -8, 8, 1], b, -8, 8, 1], k, 1, 3, 1]

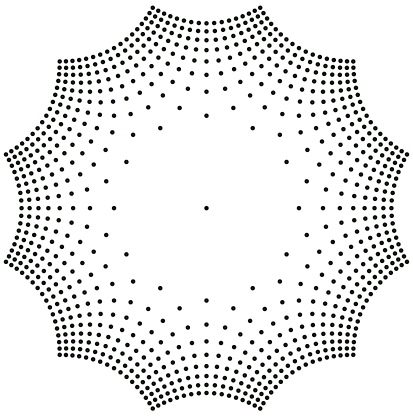
Abb. 7: Affensattel

2.8 Flamme

Eingaben:

A = 0 + 0*i

Folge[Folge[-i*(a+i*b)^4, a, 0, 12], b, 1, 12]

Abb. 8: Flamme