Hans Walser, [20221010]
Kegelschnitte abrollen
Idee und Anregung: K. H., Gö.
1 Worum geht es?
Auf einem Kegelschnitt wird ein kongruenter Kegelschnitt abgerollt. Es erscheint ein invariantes Produkt. Verallgemeinerungen der Kardioide.
2 Ellipse auf Ellipse
Auf einer Ellipse lassen wir eine kongruente Ellipse abrollen (Abb. 1).
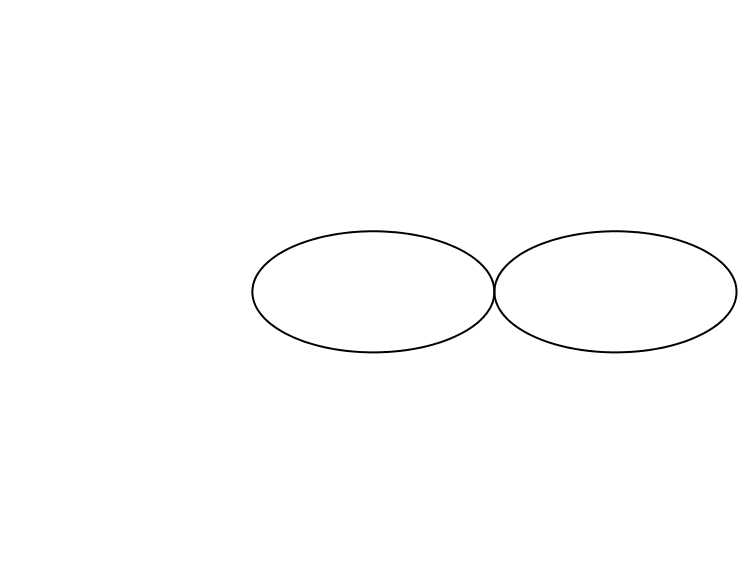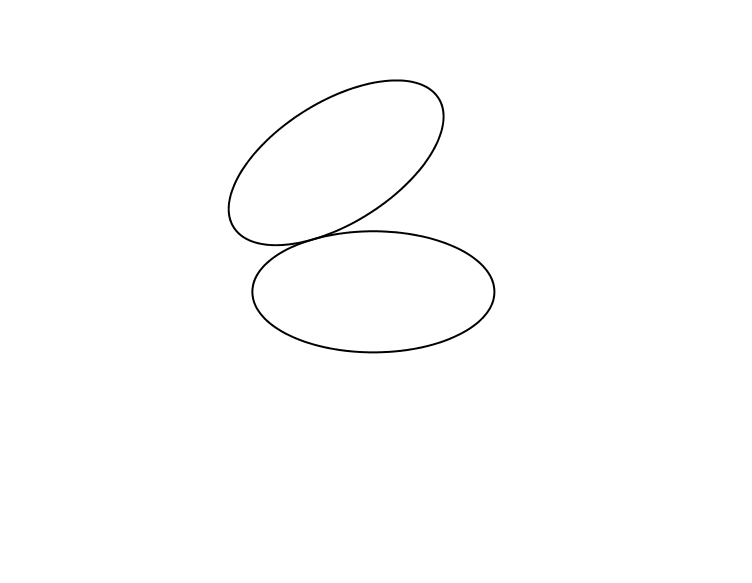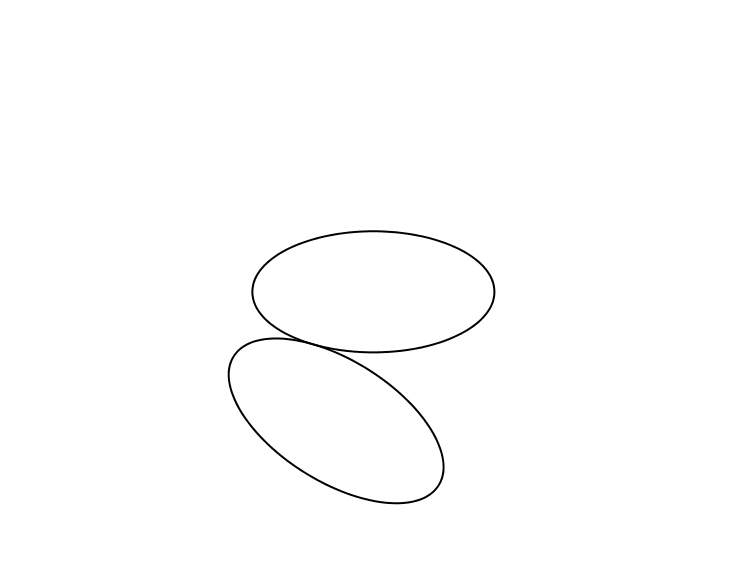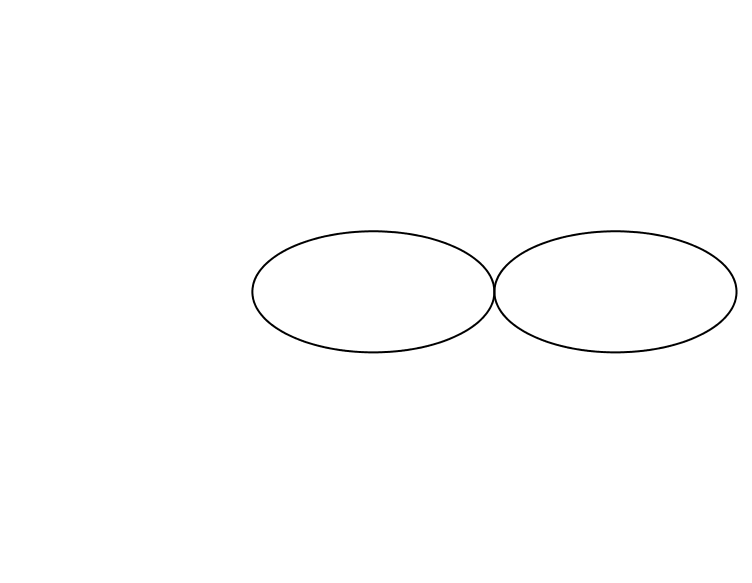
Abb. 1: Ellipse auf Ellipse
3 Gleichschenkliges Trapez
Die vier Brennpunkte der beiden Ellipsen definieren ein gleichschenkliges Trapez (Abb. 2).
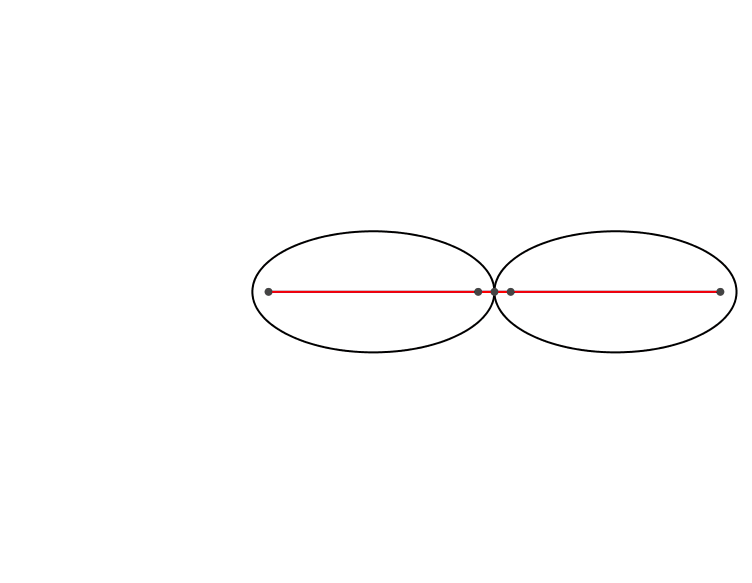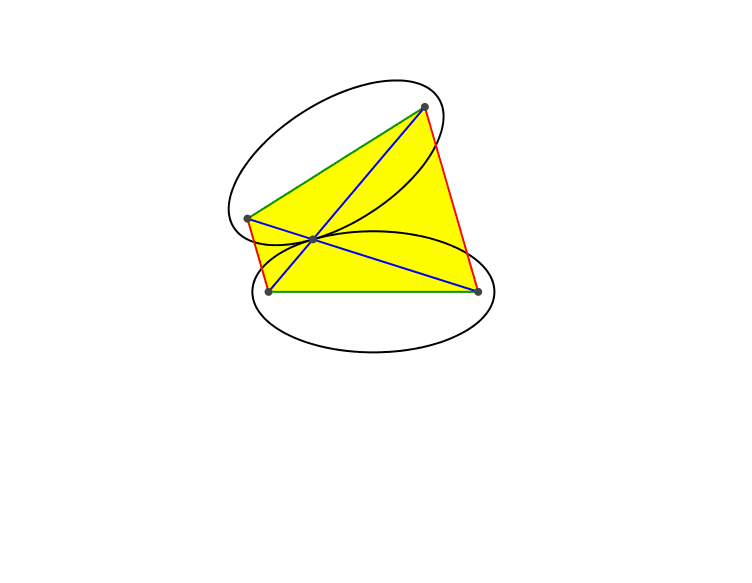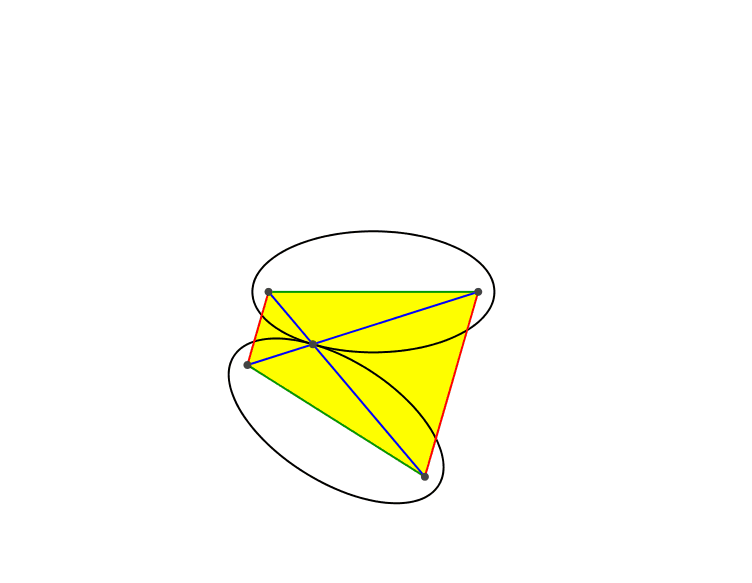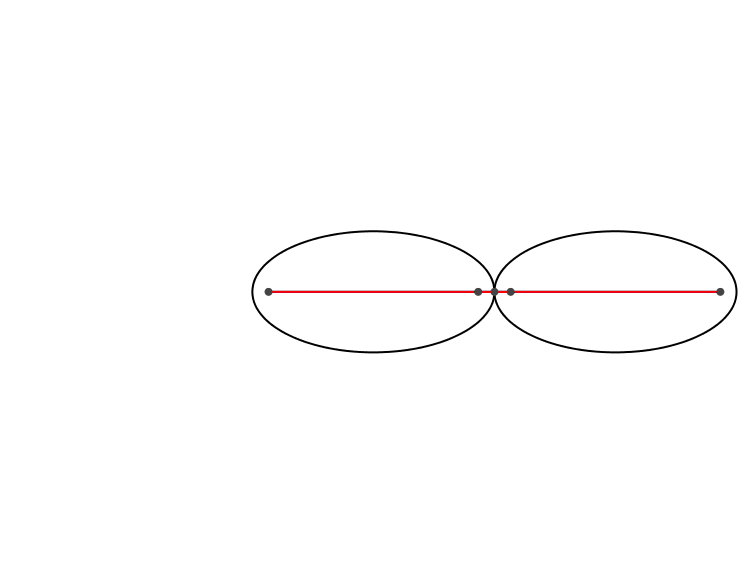
Abb. 2: Gleichschenkliges Trapez
Mit den Halbachsen a und b der Ellipsen haben diese die halbe Brennpunktweite c = √(a2 – b2).
Die beiden Schenkel (grün) des Trapezes haben die konstante Länge 2c.
Die beiden Diagonalen (blau) des Trapezes haben die konstante Länge 2a. Der Diagonalenschnittpunkt ist der Berührungspunkt der beiden Ellipsen. Dies folgt aus den Symmetrie- und Reflexionseigenschaften der Ellipse.
Die beiden Parallelseiten (rot) des Trapezes haben keine konstante Länge. Hingegen ist ihr Produkt konstant (2b)2. Dies kann mit einiger Rechnung nachgewiesen werden.
Bei der Berührung der beiden Ellipsen in den spitzen Scheiteln degeneriert das Trapez zu einer Strecke.
Bei der Berührung der beiden Ellipsen in den stumpfen Scheiteln ist das Trapez ein Rechteck mit dem Flächeninhalt 4bc.
4 Kardioiden
Die Bahnkurve eines spitzen Scheitels der abgerollten Ellipse ist ein verallgemeinerte Kardioide (Abb. 3).
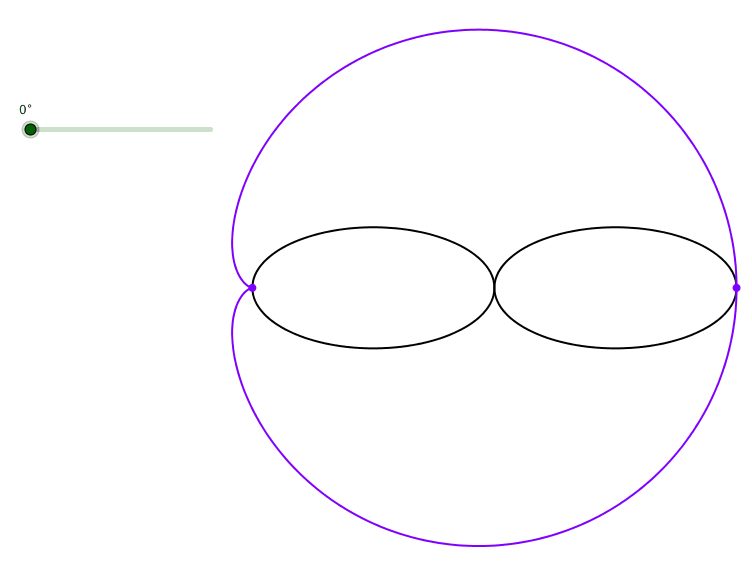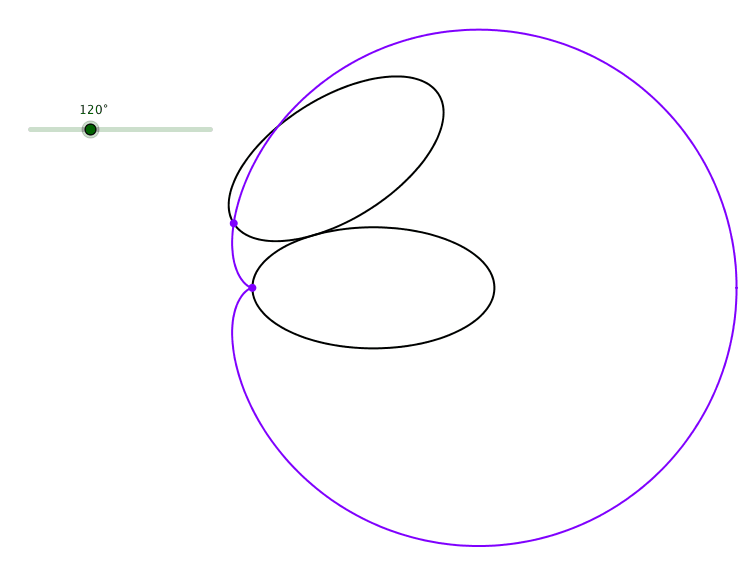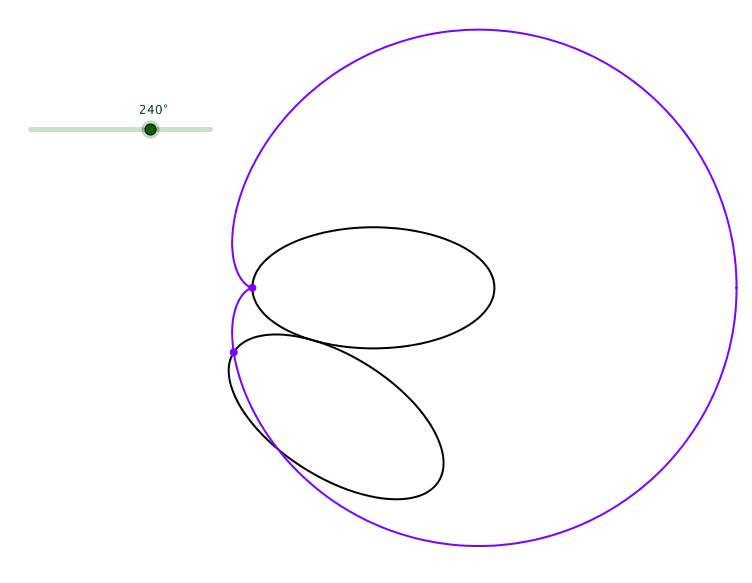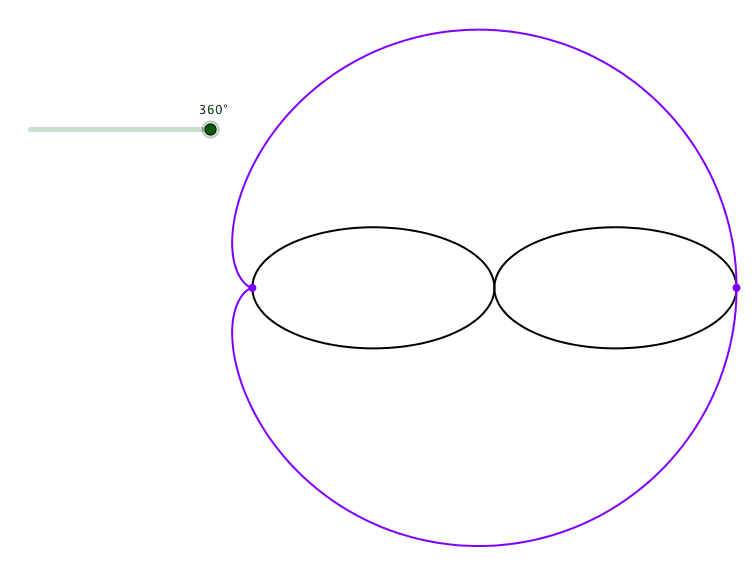
Abb. 3: Kardioide eines spitzen Scheitels
Die Bahnkurve eines stumpfen Scheitels hat eine andere Form (Abb. 4).
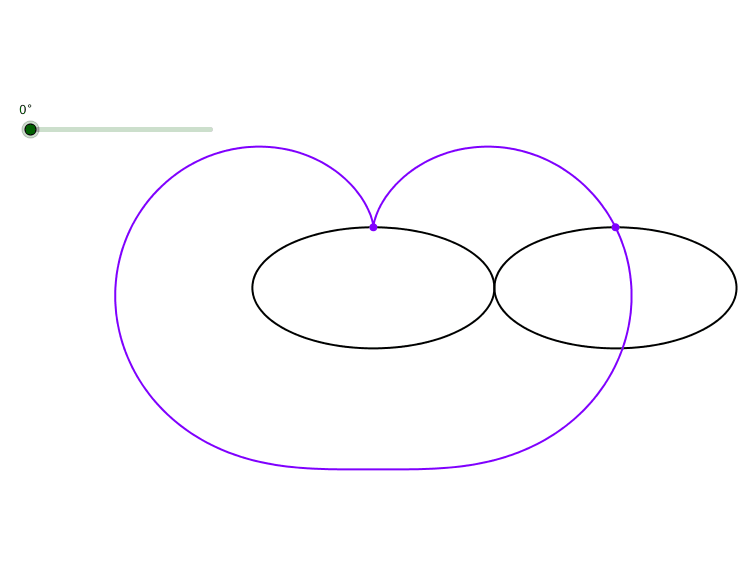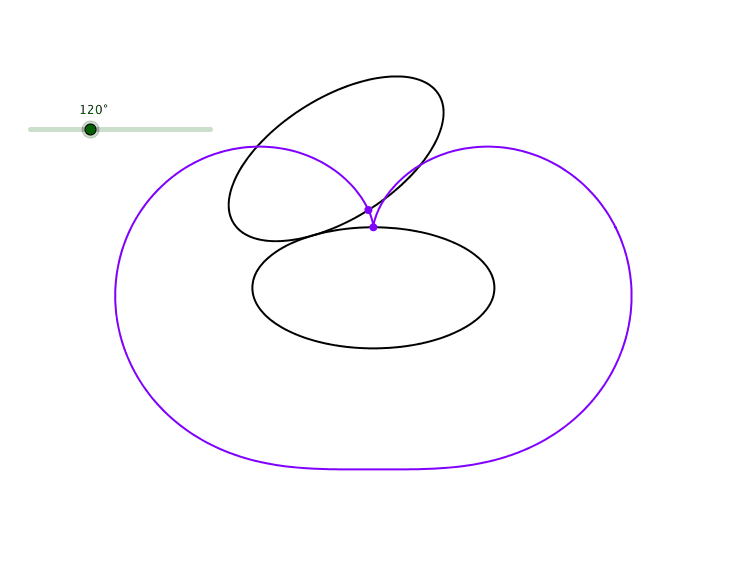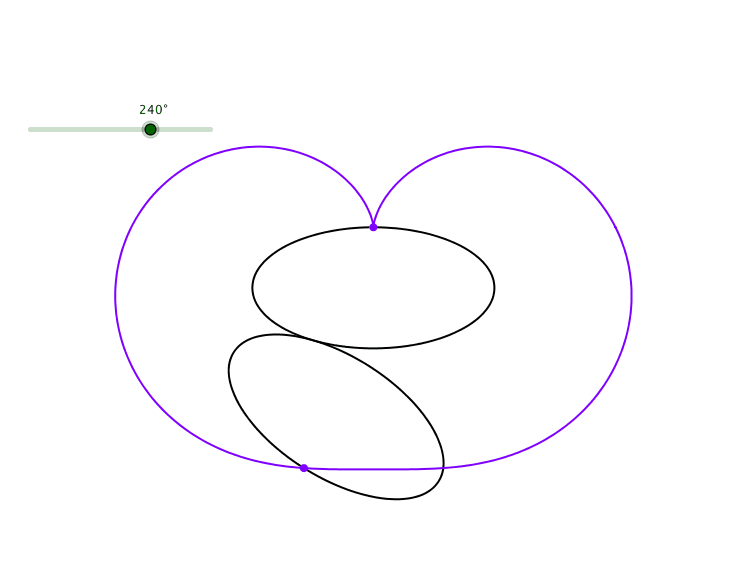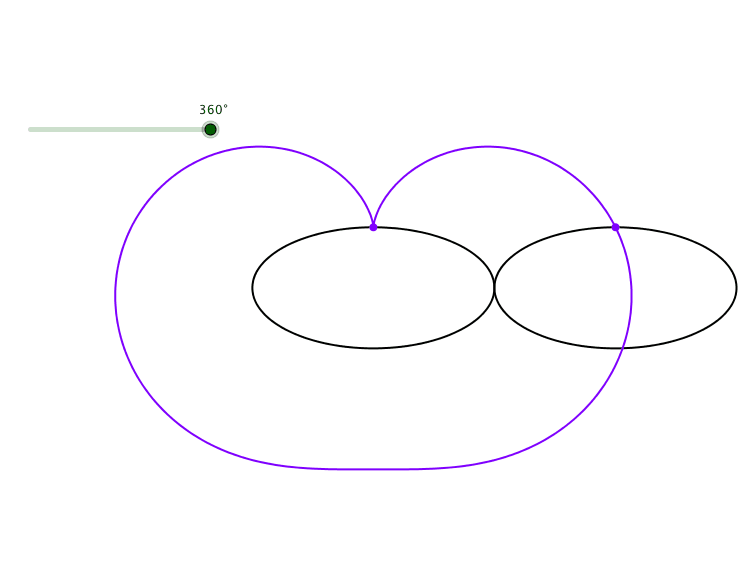
Abb. 4: Kardioide eines stumpfen Scheitels
Die Abbildung 5 zeigt eine schiefe Kardioide.
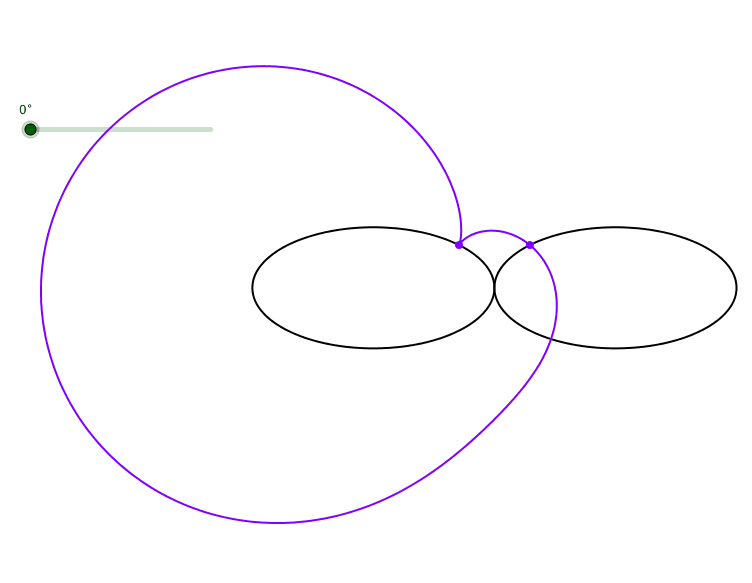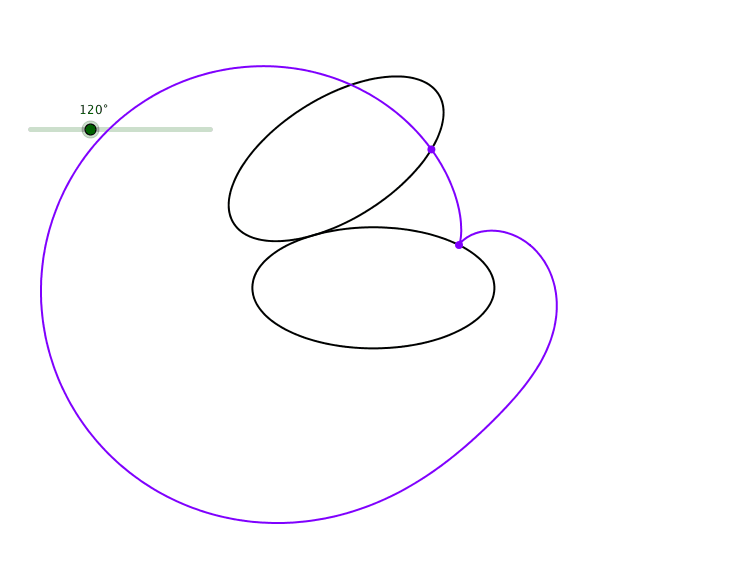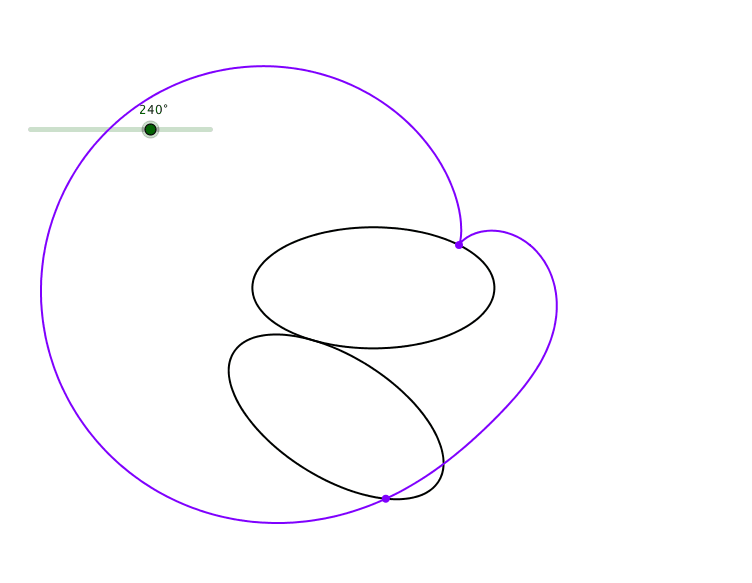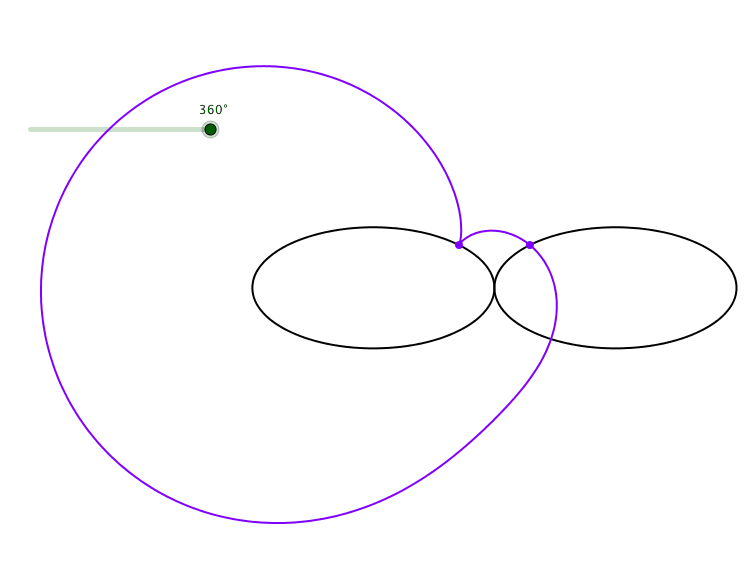
Abb. 5: Schiefe Kardioide
5 Andere Darstellung
Die Abbildung 6 gibt eine symmetrische Darstellung der beiden Ellipsen.
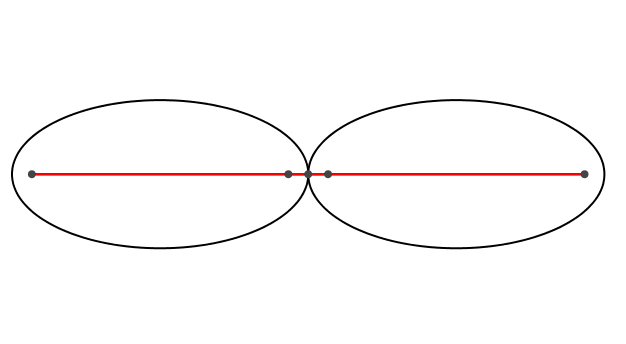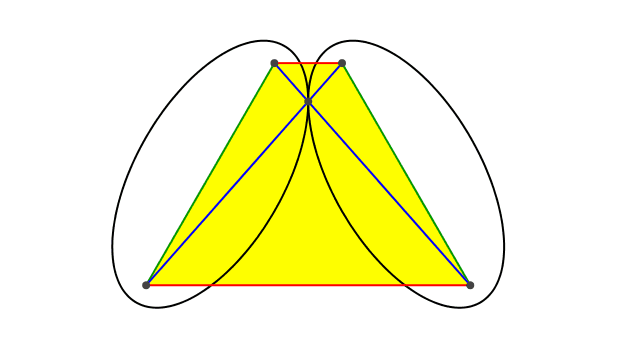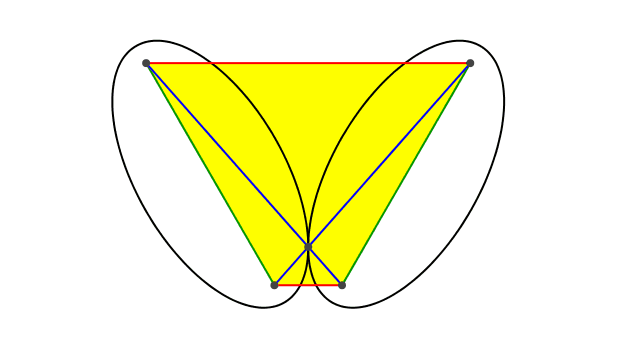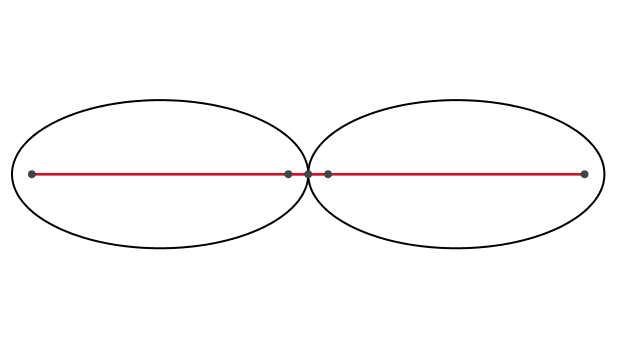
Abb. 6: Symmetrische Darstellung
Die Bahnkurven der spitzen Scheitel (die „Kardioiden“ also) haben in dieser Darstellung eine völlig andere Form (Abb. 7).
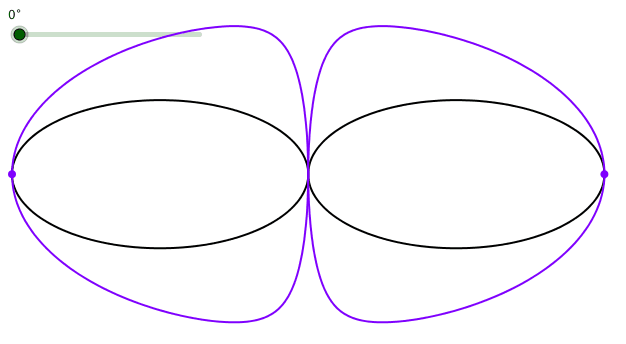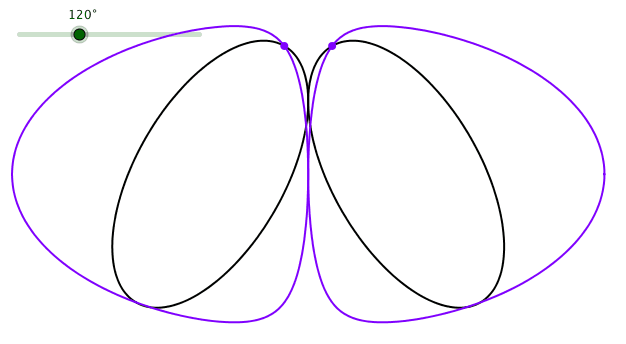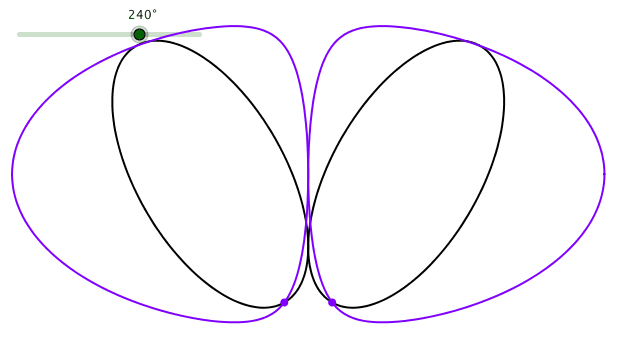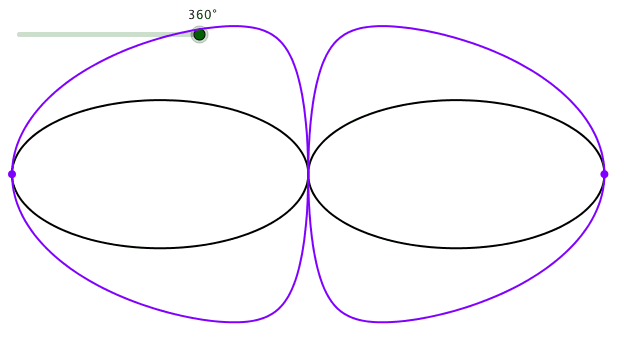
Abb. 7: „Kardioide“
6 Sonderfall. Kehrzahl
Wir wählen nun speziell die lange Halbachse a = √(1/2) ≈ 0.707 und die kurze Halbachse b = ½ = 0.5 (Abb. 8). Es ist dann auch c = ½ = 0.5.
Die Schenkel (grün) des Trapezes haben nun die konstante Länge 1, die Diagonalen (blau) die konstante Länge √2 ≈ 1.414.
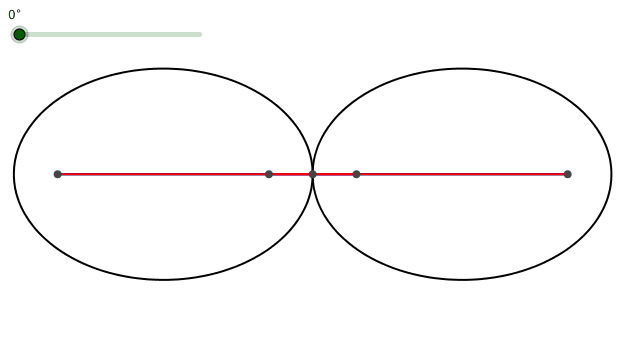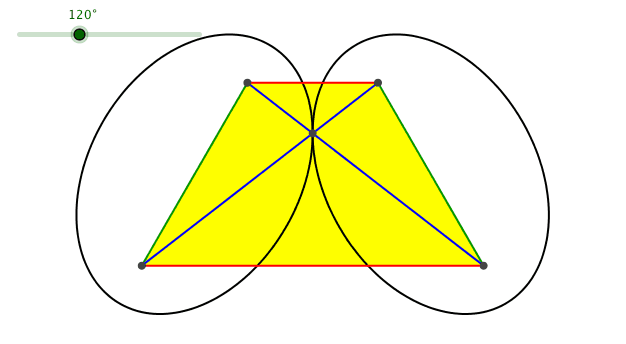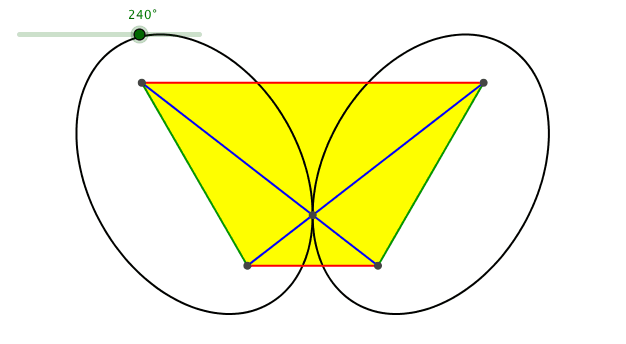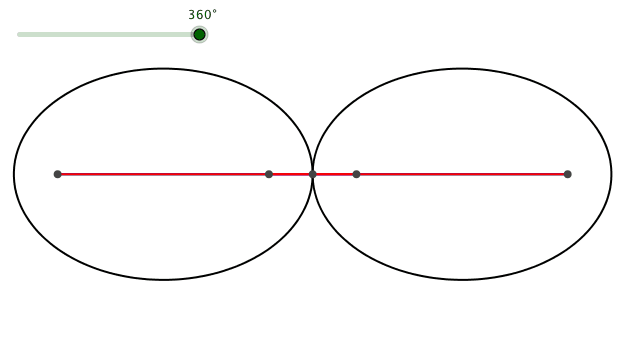
Abb. 8: Spezielle Daten
Die roten Parallelseiten des Trapezes haben das Produkt 1. Ihre Längen sind also Kehrzahlen.
Für den Animationsparameterwert 90° ergibt sich ein Quadrat mit der Seitenlänge 1 (Abb. 9).
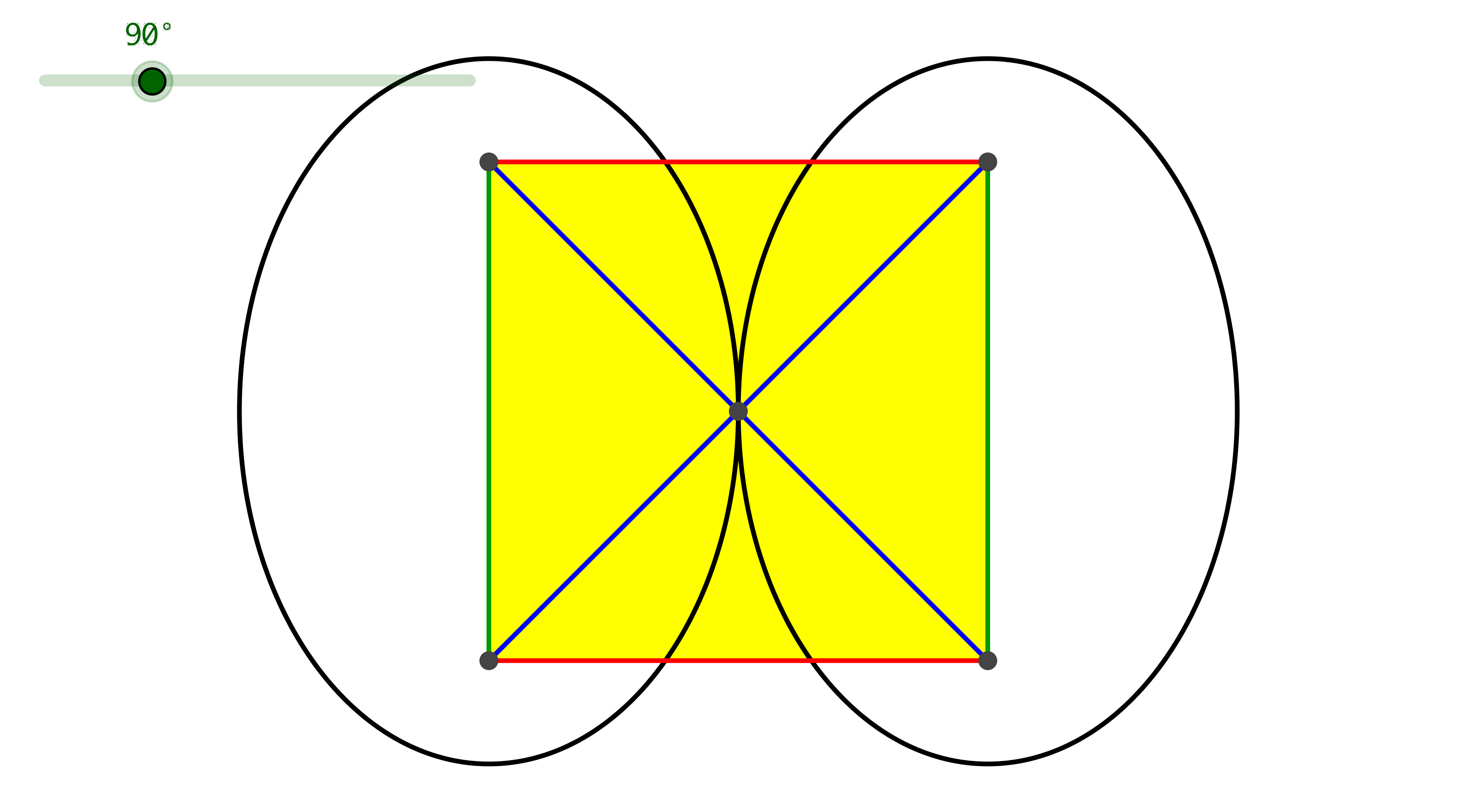
Abb. 9: Quadrat
Für den Animationsparameterwert 120° ergibt sich ein Trapez mit dem Basiswinkel 60° (Abb. 10). Die Grundparallele hat die Länge des Goldenen Schnittes Φ = (1+√5)/2 ≈ 1.618, die Deckparallel die Länge 1/Φ = (–1+√5)/2 ≈ 0.618. Dieses Trapez wird manchmal als Goldenes Trapez bezeichnet.
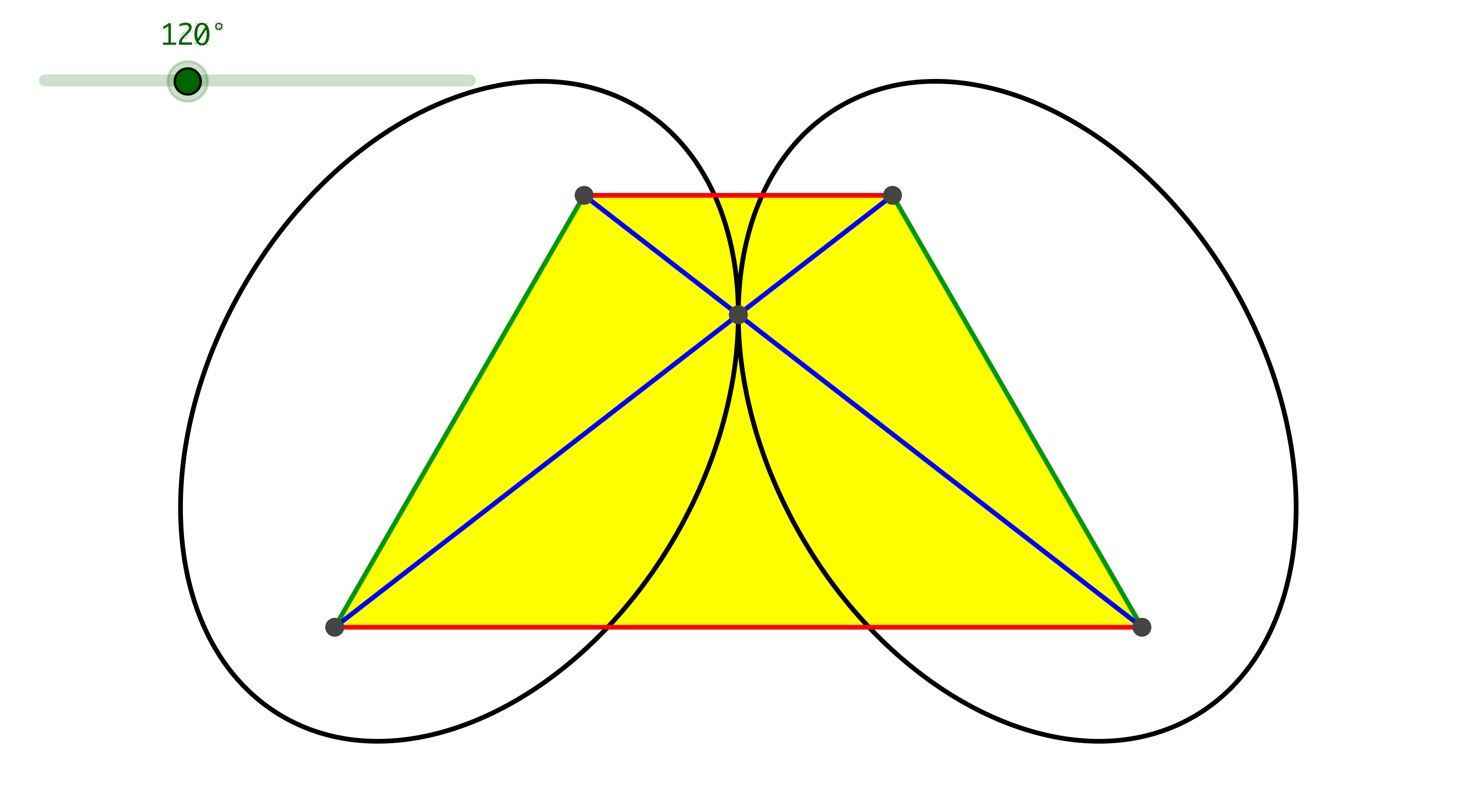
Abb. 10: Goldenes Trapez
7 Hyperbel auf Hyperbel
Das Abrollen funktioniert auch für zwei kongruente Hyperbeln (Abb. 11).
Die vier Brennpunkte der beiden Hyperbeln definieren wiederum ein gleichschenkliges Trapez.
Abb. 11: Hyperbeln
Mit den Halbachsen a und b der Hyperbeln haben diese die halbe Brennpunktweite c = √(a2 + b2).
Die beiden Schenkel (grün) des Trapezes haben nun die konstante Länge 2a. Der Schnittpunkt der Trägergeraden der beiden Schenkel ist der Berührungspunkt der beiden Hyperbeln.
Die beiden Diagonalen (blau) des Trapezes haben die konstante Länge 2c.
Die beiden Parallelseiten (rot) des Trapezes haben keine konstante Länge. Hingegen ist ihr Produkt konstant (2b)2.
Bei der Berührung der beiden Hyperbeln in den spitzen Scheiteln degeneriert das Trapez zu einer Strecke.
Der Berührungspunkt der beiden Hyperbeln muss im Unendlichen von einem Hyperbelast auf den anderen umsteigen, wie beim Zürcher Hauptbahnhof ein zeitraubendes Unterfangen. In dieser Situation ist das Trapez ein Rechteck mit dem Flächeninhalt 4bc.
Die Abbildung 12 gibt die Bahnkurve eines Scheitelpunktes. Also eine „hyperbolische Kardioide“.
Abb. 12: Bahnkurve eines Scheitelpunktes
Die Abbildung 13 zeigt den Fall der gleichseitigen Hyperbel mit a = b = ½. Im Umsteigepunkt haben wir ein Quadrat der Seitenlänge 1.
Abb. 13: Gleichseitige Hyperbel
Die zugehörige „Kardioide“ ist ein schöner Tropfen (Abb. 14).
Abb. 14: Bahnkurve eines Scheitelpunktes
8 Parabel auf Parabel
In der Abbildung 15 rollt eine Parabel auf einer liegenden Parabel ab. Der Brennpunkt der einen Parabel liegt auf der Leitlinie der anderen Parabel und umgekehrt.
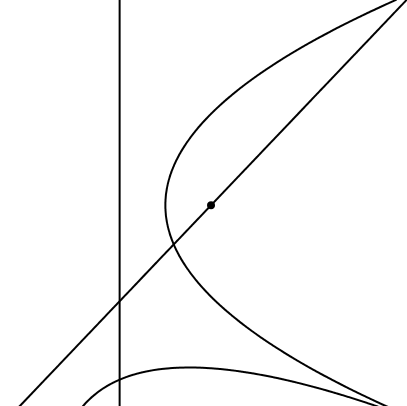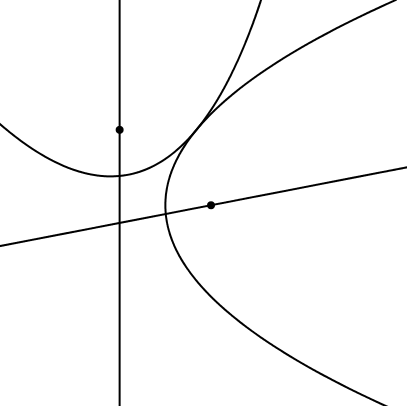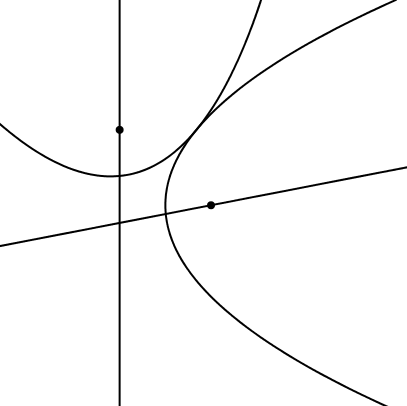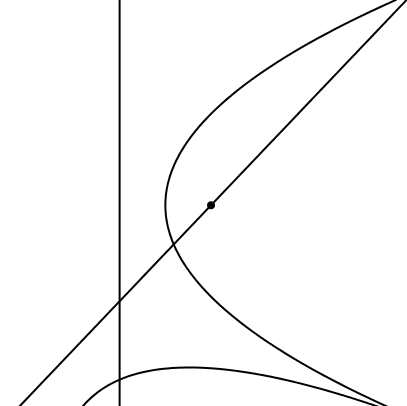
Abb. 15: Parabel auf Parabel
Die beiden Brennpunkte, der Schnittpunkt der beiden Leitlinien und der Berührungspunkt der beiden Parabeln liegen auf einem Kreis (Abb. 16).
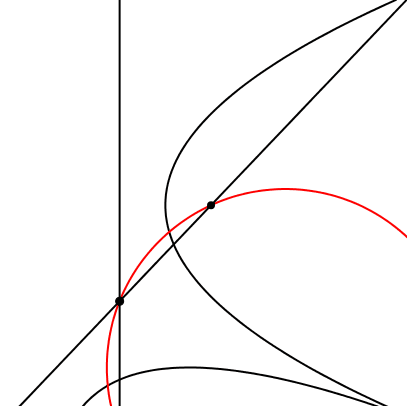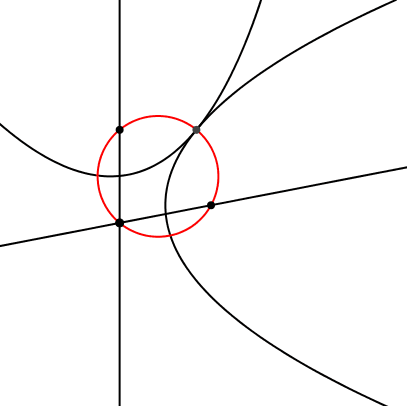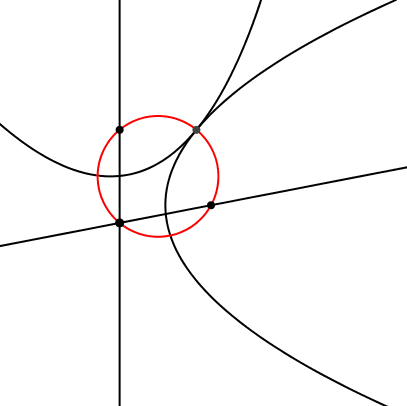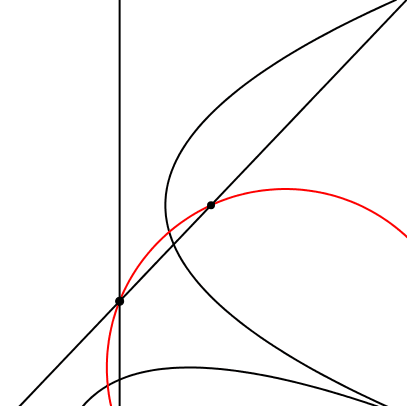
Abb. 16: Vier Punkte auf einem Kreis
Die Bahnkurve des Scheitels der abgerollten Parabel ist die Zissoide des Diokles (Abb. 17). Sie hat eine Asymptote, deren Konstruktion aus der Abbildung 17 ersichtlich ist.
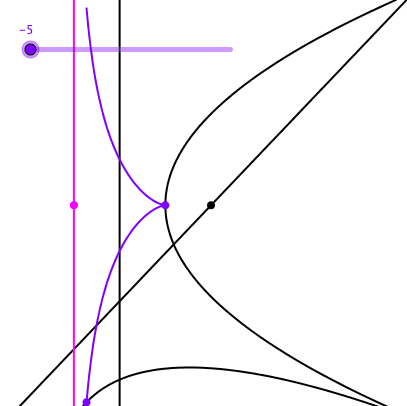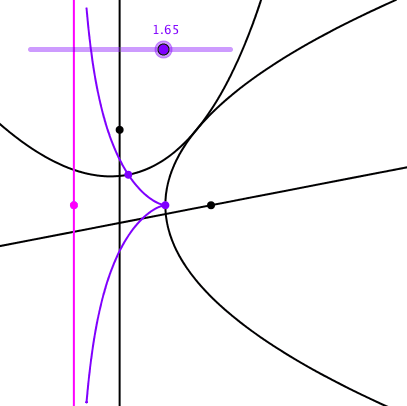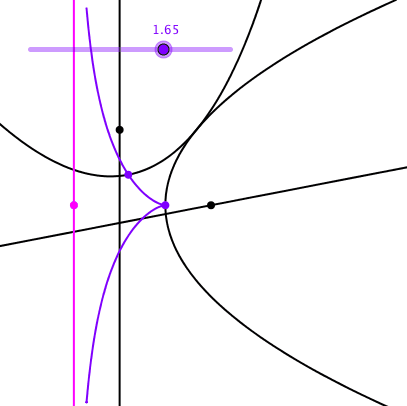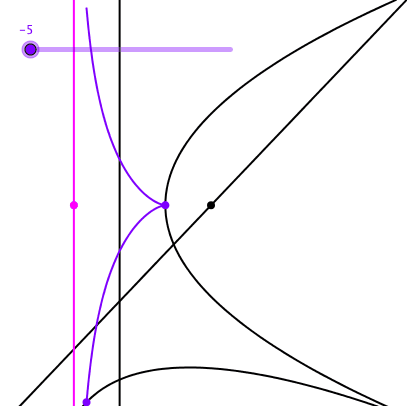
Abb. 17: Bahnkurve des Scheitelpunktes mit Asymptote
Weblinks
K.H.
https://artofproblemsolving.com/community/c2083h2933171_semi_latus_rectu
Hans Walser: Goldene Trapeze und Goldenes Sechseck
http://www.walser-h-m.ch/hans/Miniaturen/G/Goldene_Trapeze/Goldene_Trapeze.htm
Hans Walser: Goldenes Trapez
https://www.walser-h-m.ch/hans/Miniaturen/G/Goldenes_Trapez/Goldenes_Trapez.htm
Hans Walser: Kehrzahl aus Gelenkmodell
http://www.walser-h-m.ch/hans/Miniaturen/K/Kehrzahl/Kehrzahl.htm