Hans Walser, [20150225]

Kegelschnitte

1 Worum geht es

Wie erhalten wir zu einem durch eine Kurve gegebenen Kegelschnitt Brennpunkte und allenfalls Leitlinie?

2 Kreis

Die Gerade durch die Mittelpunkte zweier paralleler Sehnen liefert beim Schnitt mit der Kreislinie einen Durchmesser. Der Mittelpunkt des Durchmessers ist das Kreiszentrum (Abb. 1). Damit haben wir auch den Kreisradius.

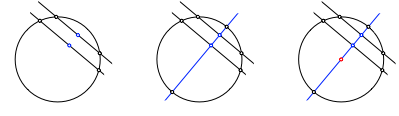
Abb. 1: Kreiszentrum und Radius

Natürlich kann alternativ mit der Mittelsenkrechten einer Kreissehne gearbeitet werden.

3 Ellipse

Die Gerade durch die Mittelpunkte zweier paralleler Sehnen liefert beim Schnitt mit der Ellipse einen Durchmesser (Abb. 2). Sein Mittelpunkt ist das Zentrum der Ellipse.

Abb. 2: Zentrum der Ellipse

Nun zeichnen wir einen Kreis um das Ellipsenzentrum, der die Ellipse in vier Punkten schneidet (Abb. 3). Die vier Punkte definieren ein Rechteck, dessen Symmetrieachsen auch die Symmetrieachsen der Ellipsen sind. So erhalten wir die Scheitel der Ellipse und die lange und die kurze Halbachse. Nun schneiden wir den Kreis um den stumpfen Scheitel mit der langen Halbachse als Radius mit der langen Ellipsenachse und erhalten so die beiden Brennpunkte.

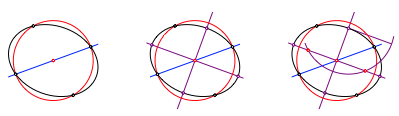
Abb.3: Achsen und Brennpunkte

4 Parabel

Die Mittelpunkte zweier paralleler Sehnen liefern eine Gerade, welche zur Symmetrieachse der Parabel parallel ist (Abb. 4). Daher ist die Mittelsenkrechte einer zu dieser Geraden senkrechten Sehne die Symmetrieachse der Parabel. Damit erhalten wir auch den Scheitelpunkt der Parabel.

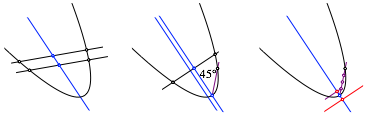
Abb. 4: Brennpunkt und Leitlinie der Parabel

Wir drehen nun die Symmetrieachse um den Scheitelpunkt um 45°. Die so entstandene Sehne teilen wir in vier gleiche Teile. Den zum Scheitelpunkt nächstliegenden Teilpunkt projizieren wir senkrecht auf die Symmetrieachse. Dies gibt den Brennpunkt der Parabel. Durch Spiegelung am Scheitelpunkt erhalten wir die Position der Leitlinie.

5 Hyperbel

Zunächst arbeiten wir wieder mit zwei parallelen Sehnen, deren Mittelpunkte einen Hyperbeldurchmesser und damit das Zentrum der Hyperbel liefern (Abb. 5).

Abb. 5: Zentrum der Hyperbel

Mit einem Kreis um das Hyperbelzentrum erhalten wir vier Hyperbelpunkte, welche ein Rechteck bilden. Dessen Symmetrieachsen sind auch Symmetrieachsen der Hyperbel (Abb. 6). Damit erhalten wir auch die beiden Scheitelpunkte und die Halbachse a.

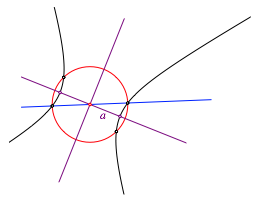
Abb. 6: Symmetrieachsen

Zur Konstruktion der anderen Halbachse, also b, tragen wir vom Zentrum aus auf der zu a gehörenden Achse ab und gehen von dort aus senkrecht zu Hyperbel (Abb. 7). So erhalten wir b.

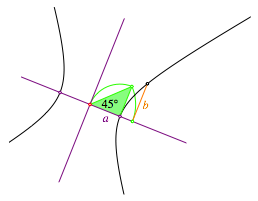
Abb. 7: Konstruktion von b

Für die halbe Brennpunktweite c bauen wir ein rechtwinkliges Dreieck mit den Katheten a und b (Abb. 8). So erhalten wir die Brennpunkte.

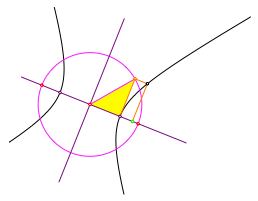
Abb. 8: Brennpunkte

Die Hypotenuse des rechtwinkligen Dreiecks liefert die eine der beiden Asymptoten der Hyperbel (Abb. 9). Die andere ist symmetrisch dazu.

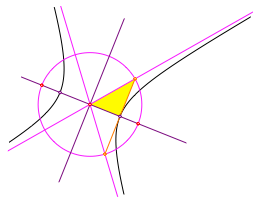
Abb. 9: Asymptoten