Hans Walser, [20130316], [20121218], [20140317b]

Kardioide und Goldener Schnitt

Anregungen: K. H., Gö. und T. S., V.

1 Worum geht es?

In der Kardioide erscheint durch den Schnitt mit einer geeigneten Geraden der Goldene Schnitt.

2 Die Kardioide

Die Abbildung 1 zeigt die Kardioide.

Abb. 1: Kardioide

Für die Parameterdarstellung verwenden wir das Koordinatensystem der Abbildung 2.

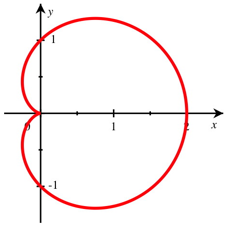
Abb. 2: Koordinatensystem

In diesem Koordinatensystem hat die Kardioide die Parameterdarstellung:

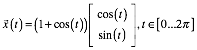
Die Kardioide ist eine Rollkurve. Auf dem grünen Kreis der Abbildung 3 rollt der gelbe Kreis ab. Ein Punkt auf dem Rand des gelben Kreises beschreibt die Kardioide.

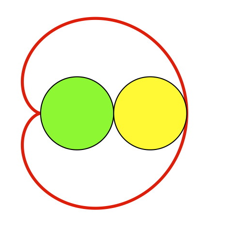
Abb. 3: Rollkurve

In der Position der Abbildung 3 ist der Schreibstift der Punkt ganz rechts auf dem Rand des gelben Kreises.

3 Die Gerade

Wir zeichnen nun die gemeinsame Tangente der beiden Kreise gemäß Abbildung 4.

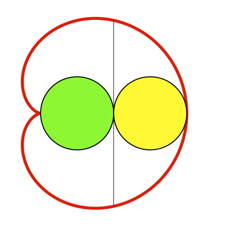
Abb. 4: Gemeinsame Tangente

4 Das Dreieck

Und schließlich ergänzen wir zum rechtwinkligen Dreieck gemäß Abbildung 5.

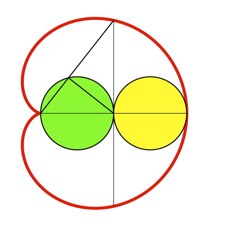
Abb. 5: Rechtwinkliges Dreieck

Dieses Dreieck hat es in sich. Wir arbeiten wieder mit dem oben angegebenen Koordinatensystem (Abb. 6).

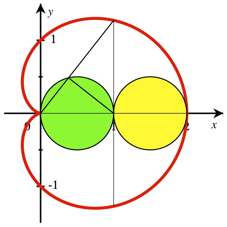
Abb. 6: Koordinatensystem

5 Der Goldene Schnitt

Es gelten die in der Abbildung 7 angegebenen Längen.

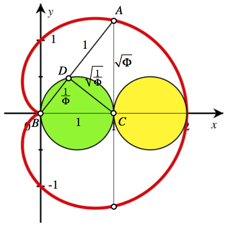
Abb. 7: Längen

Der Goldene Schnitt [Walser 2013]

erscheint an vielen Orten.

6 Beweise

Das rechtwinklige Dreieck ABC hat gemäß Disposition die Kathete . Für den Punkte A haben wir die Koordinaten . Da der Punkt auf der Kardioide liegt, muss gelten:

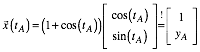
Somit ist:

Diese quadratische Gleichung für hat die Lösung:

Hier erscheint der Goldene Schnitt in der Rechnung. Allerdings ist

keine „schöne“ Zahl. Nun ist aber:

Weiter gilt für die Hypotenuse c des rechtwinkligen Dreiecks ABC:

Daraus ergibt sich für die Höhe h des Dreiecks ABC:

Damit erhalten wir schließlich:

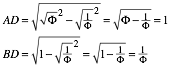
Damit sind die in der Abbildung angegebenen Längen verifiziert.

7 Dreiecksraster

In der Abbildung 8 ist ein den Kreisen angepasstes Dreiecksraster eingezeichnet. Wir sehen, dass die Extrempunkte der Kardioide (höchster und tiefster Punkt, Punkte ganz links und ganz rechts) Rasterpunkte sind.

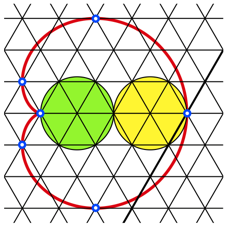
Abb. 8: Dreiecksraster mit Extrempunkten

Der Beweis ergibt sich durch Nachrechnen. Die eingezeichneten blauen Punkte gehören zu den Parameterwerten:

8 Nochmals der Goldene Schnitt

Wir zeichnen den Inkreis in die Kardioide. Zusammen mit dem grünen Kreis und den Extrempunkten ergibt sich der Goldene Schnitt (Abb. 9). Die Majore sind blau, die Minore rot eingezeichnet. Beweis durch Nachrechnen oder geschickte Anwendung der Figur von Odom.

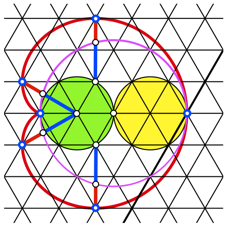
Abb. 9: Der Goldene Schnitt

Literatur

[Walser 2013] Walser, Hans: Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Edition am Gutenbergplatz, Leipzig 2013. ISBN 978-3-937219-85-1