Hans Walser, [20160211]
Kantenschwerpunkt im Viereck
1 Worum geht es?
Es wird eine Konstruktion fźr den Kantenschwerpunkt im Viereck angegeben. Zudem wird gezeigt, dass genau im Parallelogramm der Kantenschwerpunkt mit dem Eckenschwerpunkt zusammenfŠllt.
†ber Schwerpunkte im Viereck siehe (Fritsch und Pickert, 2014).
2 Bezeichnungen
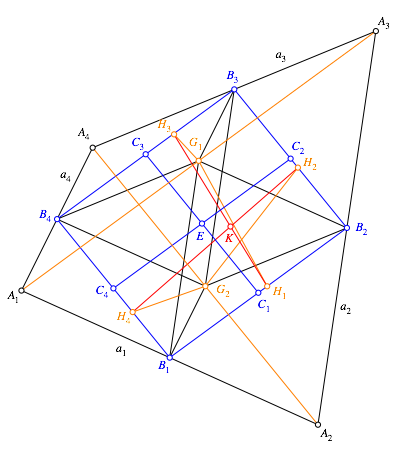
Abb. 1: Bezeichnungen
Die Abbildung 1 zeigt die im Folgenden verwendeten Bezeichnungen.
Das
Viereck 
hat die
Seiten 
(Zyklische
Indizierung). 
ist der
Mittelpunkt der Strecke 
. 
ist der
Mittelpunkt der Strecke 
. 
ist der Mittelpunkt
der Diagonale 
. 
, ist der Schnittpunkt der Winkelhalbierenden des
Winkels 
mit der
Geraden 
. 
, ist der Schnittpunkt der Winkelhalbierenden des
Winkels 
mit der
Geraden 
.
3 Der Kantenschwerpunkt
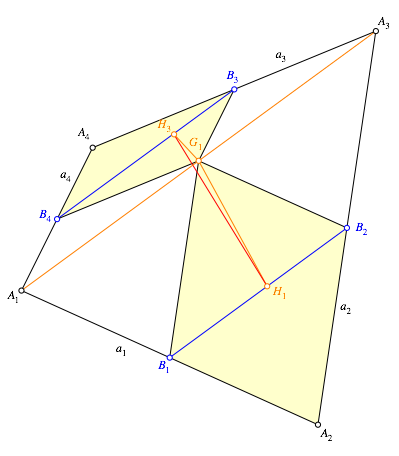
Abb. 2: Winkelhalbierende
Die
Winkelhalbierende des Winkels 
schneidet
die Strecke 
im Punkt 
. Die Abschnitte von diesem Schnittpunkt zu den
Endpunkten der Strecke sind daher im VerhŠltnis der anliegenden Seiten des
Dreiecks 
und damit
auch im umgekehrten VerhŠltnis zu den StreckenlŠngen 
und 
. Es ist also:
(1)
Damit ist
der
Schwerpunkt der beiden Viereckseiten 
und 
.
Analog
ist 
der
Schwerpunkt der Viereckseiten 
und 
.
(2)
Der
Schwerpunkt aller vier Viereckseiten (also der so genannte Kantenschwerpunkt
des Viereckes) liegt daher auf der Geraden 
.
Analog
liegt der Kantenschwerpunkt K auf der
Geraden 
und ist
daher der Schnittpunkt dieser beiden Geraden (Abb. 3).
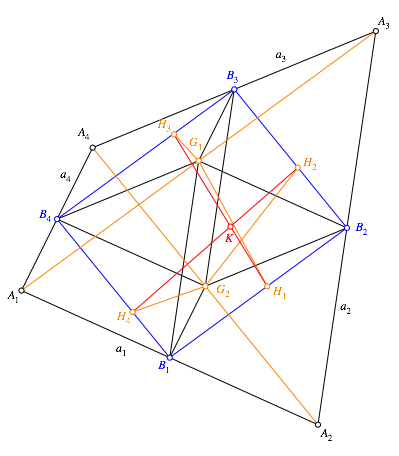
Abb. 3: Kantenschwerpunkt
4 Der Eckenschwerpunkt
Der
Eckenschwerpunkt E ist der
Mittelpunkt des Parallelogramms 
und kann
zum Beispiel als Schnittpunkt der Strecken 
und 
gefunden
werden (Abb. 4). Er ist auch der Mittelpunkt dieser Strecken.
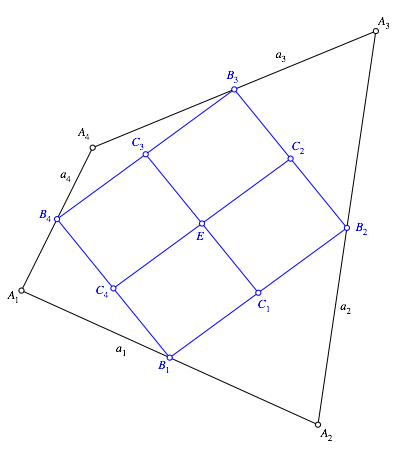
Abb. 4: Eckenschwerpunkt
5 Kantenschwerpunkt = Eckenschwerpunkt?
In der Regel sind K und E verschieden.
Im Fall 
muss die Strecke
durch E verlaufen. Aus Symmetriegrźnden muss
dann
(3)
Damit wird:
(4)
Wegen (1) und (2) hei§t das:
(5)
Analog:
(6)
Durch Dividieren erhalten wir aus (5) und (6):
(7)
Aus (7) fźr die positiven KantenlŠngen:
(8)
Analog folgt auch die Gleichheit der beiden anderen Seiten. Das Viereck ist ein Parallelogramm.
Literatur
Fritsch, Rudolf und Pickert, Gźnter (2014): Schwerpunkte von Vierecken. Die Wurzel, Heft 2 / 2014, 35-41.