Hans Walser, [20170514]
Jonas zerlegt Gau§
1 Die Anekdote
Vom kleinen Gau§ geht die Anekdote, er habe in der Schule die Zahlen von 1 bis n zusammenzhlen mssen. Die Anekdote existiert in drei Varianten, nmlich fr die Obergrenzen 40, 60 und 100:
![]() (1)
(1)
In der Schule wird meistens die dritte Variante kolportiert. Vielleicht haben die Schulmeister eine professionelle Affinitt zum Dezimalsystem, obwohl dies im Kontext der Aufgabe keine Rolle spielt.
2 Die bliche Visualisierung
Es wird mit kreisrunden Punkten (Humanistisch angehauchte Lehrpersonen reden von Calculi, Kieselsteinen also, die anderen von Zhlpfennigen) gearbeitet, die in einem Quadratraster angeordnet werden. Weil 100 dann ab er doch eine gar gro§e Zahl ist, macht man es mit 10 (Abb. 1).
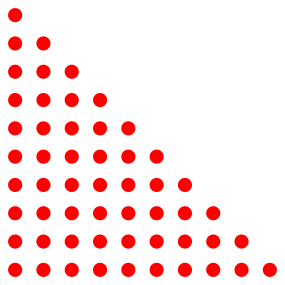
Abb. 1: Summe der Zahlen von 1 bis 10
Und dann wird mit einem der blichen Tricks (Dreiecksflche mit Korrekturen, Ergnzung zu Rechteck oder Quadrat) die Formel hergeleitet.
Die Summe der Zahlen von 1 bis 10 ist allerdings noch berschaubar und kann im Kopf berechnet werden. Wir brauchen die Formel nicht. Ich komme auf 55.
3 Die Idee von Jonas
Wir nehmen zehnmal die Treppe der Abbildung 1. Das ist aber nur die Feinabstimmung. Als Unterbau fahren wir ein grberes Kaliber auf (Abb. 2).
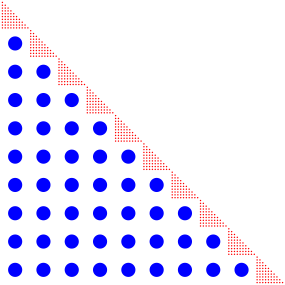
Abb. 2: Idee von Jonas
Ein blauer Punkt entspricht 102 = 100 roten Punkten. Die blauen Punkte bilden ihrerseits eine Treppe, allerdings mit nur 9 Stufen. Die Summe der Zahlen von 1 bis 9 ist 45. Wir haben also 45 blaue Punkte. Das ist noch berschaubar und kann ohne Formel berechnet werden.
Nun knnen wir frhlich weiterrechnen:
![]() (2)
(2)
4 Loslsung vom Dezimalsystem
Die obige Darstellung ist offensichtlich am Dezimalsystem orientiert. Dies ist aber nicht zwingend. Als Gegenbeispiel berechnen wir die Summe der Zahlen von 1 bis 40, wobei wir 40 in die Faktoren 5 und 8 zerlegen.
Die Summe der Zahlen von 1 bis 5 ist 15 (Kopfrechnung) (Abb. 3).

Abb. 3: Die Summe der Zahlen von 1 bis 5
Die Idee von Jonas fhrt auf die Darstellung der Abbildung 4. Ein blauer Punkt entspricht 52 = 25 roten Punkten. Die Treppe der blauen Punkte ist (8 – 1) = 7 Stufen hoch. Somit ist die Anzahl der blauen Punkte die Summe der Zahlen von 1 bis 7, also 28.
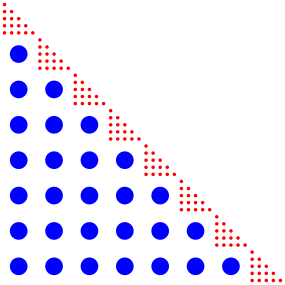
Abb. 4: Idee von Jonas
Daher erhalten wir:
![]() (3)
(3)
5 Allgemein
Es soll die Summe der natrlichen Zahlen von 1 bis n berechnet werden, wobei die Zahl n keine Primzahl ist, sondern in zwei Faktoren n = pq zerlegt werden kann. Die beiden Faktoren p und q brauchen keine Primzahlen zu sein.
Natrlich mssen wir jetzt mit der Formel arbeiten.
Fr feine rote Treppe, also die Summe der Zahlen von 1 bis p gilt:
![]() (4)
(4)
Ein blauer Punkt des Unterbaues entspricht p2 roten Punkten.
Die blaue Treppe hat (q – 1) Stufen. Damit erhalten wir fr die Anzahl der blauen Punkte:
![]() (5)
(5)
Fr die Summe der Zahlen von 1 bis n ergibt sich nun:
![]() (6)
(6)
Damit haben wir die bliche Formel wieder erhalten.
6 Didaktischer Kommentar
Wir sind hier mit der Kirche ums Dorf gefahren. Wir haben im Kreis herum gerechnet. Die Formel (6) wurde bei (4) und (5) bereits eingesetzt. Es geht hier aber nicht darum, diese Formel herzuleiten. Wir wollen vielmehr zeigen, dass die Idee von Jonas in sich stimmig ist.
Natrlich geht es auch fr eine Zerlegung der Obergrenze n in drei Faktoren n = pqr. Es ist:
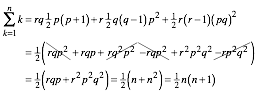 (7)
(7)
7 Herleitung der Formel
Tatschlich kann aber sehr wohl die Formel fr die Summe der ersten n natrlichen Zahlen aus der Idee von Jonas hergeleitet werden. Das geht wie folgt.
Wir gehen davon aus, dass wir die Formel nicht kennen und fhren eine vorerst unbekannte Funktion f ein:
![]() (8)
(8)
Wir verwenden lediglich:
![]() (9)
(9)
Aus der Idee von Jonas ergibt sich fr die unbekannte Funktion f die Funktionalgleichung:
![]() (10)
(10)
7.1 Rekursives Vorgehen
Aus (10) erhalten wir zunchst:
![]() (11)
(11)
Wegen (9) ergibt sich die Rekursionsformel:
![]() (12)
(12)
Zusammen
mit dem Startwert (9) kann nun ![]() rekursiv
berechnet werden. Wir haben das Zhlen neu erfunden.
rekursiv
berechnet werden. Wir haben das Zhlen neu erfunden.
7.2 Potenzreihen-Ansatz
Fr f machen wir einen formalen Potenzreihen-Ansatz:
![]() (13)
(13)
Aus (10) ergibt sich damit:
![]() (14)
(14)
Wir schreiben die beiden Seiten detailliert.
![]() (14)
(14)
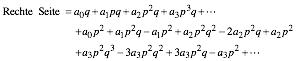 (15)
(15)
Und nun ein gezielter Koeffizientenvergleich.
Das Absolutglied kommt nur links vor:
![]() (16)
(16)
Der Koeffizient von p2 kommt nur rechts vor:
![]() (17)
(17)
Der Koeffizient von pjq, j > 2, kommt nur rechts vor:
![]() (18)
(18)
Wegen (16) und (18) verschwinden alle aj au§er a1 und a2. Wegen (17) ist dann:
![]() (19)
(19)
Es bleibt der Restansatz:
![]() (20)
(20)
Aus (9)
ergibt sich schlie§lich ![]() . Somit erhalten wir:
. Somit erhalten wir:
![]() (21)
(21)
Das warÕs.