Hans Walser, [20240312]

Inkreismittelpunkt

1 Worum es geht

Konstruktion von Inkreismittelpunkt und Inkreis ohne Winkelhalbierende

2 Konstruktion

Zu einem beliebigen Dreieck (Abb. 1) soll der Inkreismittelpunkt gefunden werden.

Abb. 1: Startdreieck

Dazu zeichnen wir den Umkreis (Abb. 2).

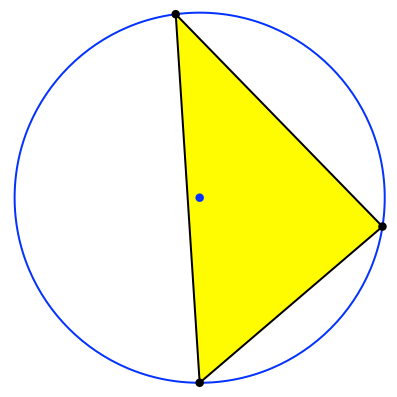
Abb. 2: Umkreis

Nun halbieren wir die Kreisbögen des Umkreises zwischen zwei Dreiecksecken. Die Mittelpunkte der Kreisbögen (rot in Abb. 3) finden wir mit den Mittelsenkrechten der Dreiecksseiten.

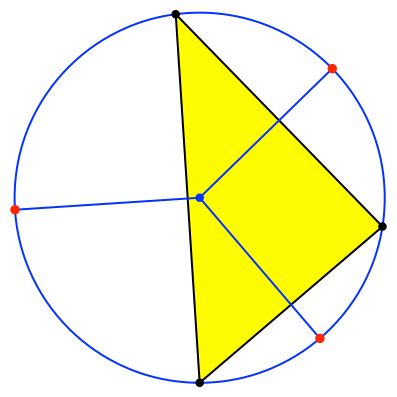
Abb. 3: Mittelpunkte der Umkreisbögen

Die Mittelpunkte der Umkreisbögen verbinden wir zu einem Dreieck (rot in Abb. 4).

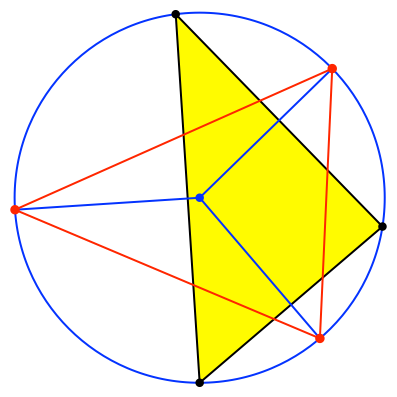
Abb. 4: Dreieck der Mittelpunkte

Wir zeichnen den Höhenschnittpunkt des roten Dreiecks (Abb. 5).

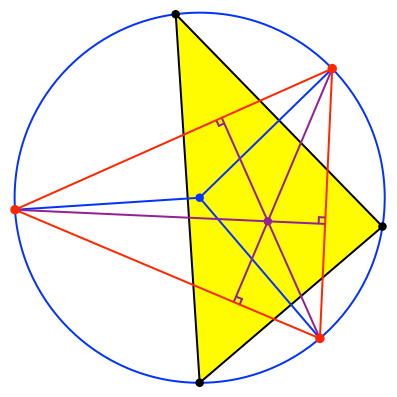
Abb. 5: Höhenschnittpunkt

Dieser Höhenschnittpunkt ist der Inkreismittelpunkt des Startdreiecks, wie Figura zeigt (Abb. 6).

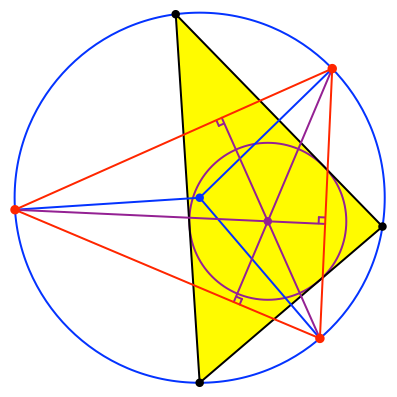
Abb. 6: Inkreismittelpunkt

3 Beweis

Für den Beweis beginnen wir mit einem Dreieck und seinen Höhen (Abb. 7).

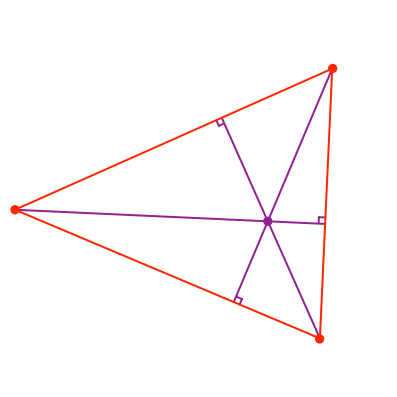
Abb. 7: Dreieck mit Höhen

Wir zerlegen das Dreieck mit Hilfe der Höhen in drei Teildreiecke (Abb. 8). Der Winkel eines Teildreiecks beim Höhenschnittpunkt ist der Ergänzungswinkel auf 180° des Winkels an der nicht an diesem Teildreieck beteiligten Dreiecksecke.

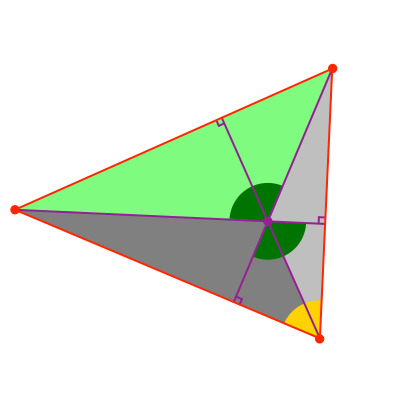
Abb. 8: Teildreiecke. Ergänzungswinkel

Wir spiegeln eines der drei Teildreiecke an der zugehörigen Dreiecksseite (Abb. 9).

Abb. 9: Hinausspiegeln

Der dunkelgrüne und der goldfarbene Winkel ergänzen sich auf 180°. Das Viereck ist also ein Sehnenviereck und hat einen Umkreis (Abb. 10).

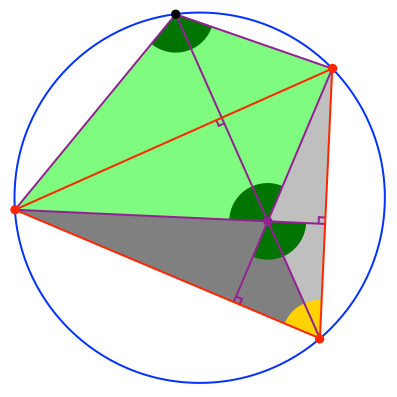
Abb. 10: Umkreis

Entsprechend können wir die beiden anderen Teildreiecke hinausspiegeln (Abb. 11). Wir erhalten ein Sechseck mit einem Umkreis.

Zusammengefasst: Wird bei einem beliebigen Dreieck der Höhenschnittpunkt an den Dreiecksseiten hinausgespiegelt, liegen die Spiegelpunkte auf dem Umkreis des Dreiecks.

Abb. 11: Sechseck mit Umkreis

Aus Symmetriegründen sind die beiden in der Abbildung 12 magenta und orange markierten Winkel gleich.

Abb. 12: Gleiche Winkel

Wir verbinden nun die herausgespiegelten Höhenschnittpunkte zu einem Dreieck (schwarz in Abb. 13). Wir wollen zeigen, dass die Höhen des roten Dreiecks die Winkelhalbierenden des schwarzen Dreiecks sind.

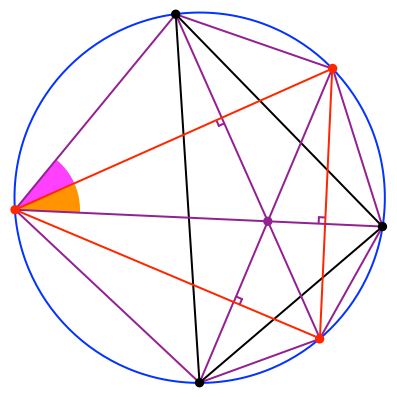
Abb. 13: Schwarzes Dreieck

Die beiden magenta markierten Winkel (Abb. 15) sind Peripheriewinkel über dem gleichen Bogen. Sie sind daher gleich.

Abb. 14: Gleiche Winkel

Die beiden orange markierten Winkel (Abb. 15) sind als Peripheriewinkel über gleichem Bogen ebenfalls gleich.

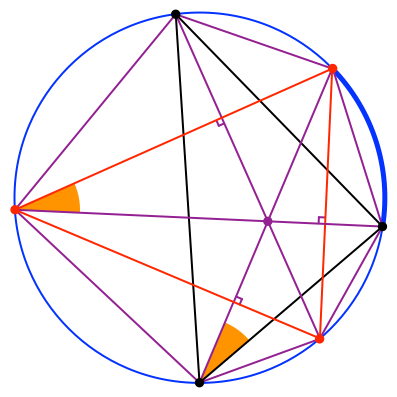
Abb. 15: Ebenfalls gleiche Winkel

Da die magenta und orange markierten Winkel gleich sind, haben wir eine Höhe des roten Dreiecks als Winkelhalbierende des schwarzen Dreiecks.

Abb. 16: Winkelhalbierende

Entsprechend für die beiden anderen Höhen des roten Dreiecks. Der Höhenschnittpunkt des roten Dreiecks ist der Inkreismittelpunkt des schwarzen Dreiecks.

Links

Hans Walser: Inkreis und Umkreis

https://walser-h-m.ch/hans/Miniaturen/I/Inkreis_und_Umkreis/Inkreis_und_Umkreis.html

Hans Walser: Vortrag: Der Inkreis

https://walser-h-m.ch/hans/Vortraege/20231118/index.html