Hans Walser, [20240313]

Inkreis und Umkreis

Anregung: Thomas Jahre, Chemnitz

1 Worum es geht

Spielerei im Dreieck mit Inkreis und Umkreis.

Zwölfpunktekreis.

Auflistung von Phänomenen. Beweise fehlen, Verifikation mit DGS.

2 Konstruktion

In einem beliebigen Dreieck zeichnen wir den Inkreis und den Umkreis (Abb. 1).

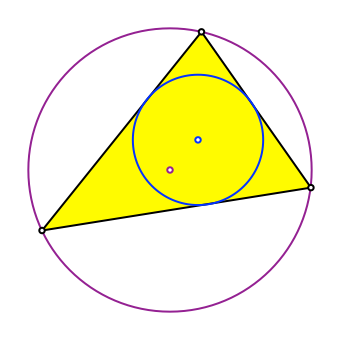
Abb. 1: Inkreis und Umkreis

Wir zeichnen die Verbindungsstrecke vom Inkreismittelpunkt zu einer Ecke und die Mittelsenkrechte dazu (Abb. 2).

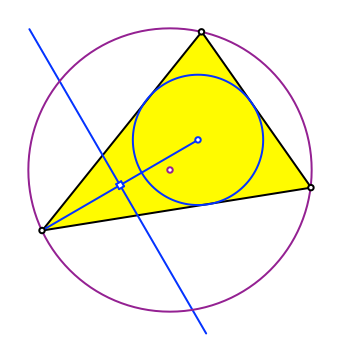
Abb. 2: Mittelsenkrechte

Dasselbe tun wir auch mit den beiden anderen Ecken (Abb. 3).

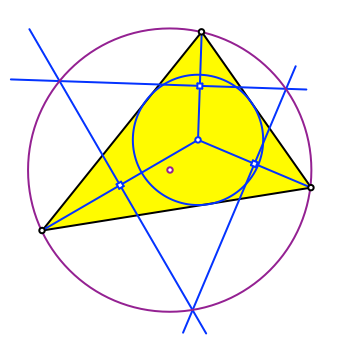
Abb. 3: Drei Mittelsenkrechte

Je zwei Mittelsenkrechte schneiden sich auf dem Umkreis (Abb. 4). Wir erhalten ein blaues Dreieck mit demselben Umkreis wie das gelbe Startdreieck.

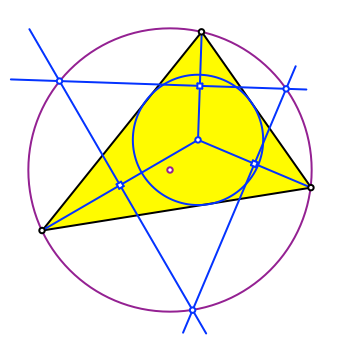
Abb. 4: Schnittpunkte auf Umkreis

Diese Schnittpunkte haben es in sich. Sie halbieren die Umkreisbögen zwischen zwei Eckpunkten des Dreiecks. Die Winkelhalbierenden des Dreiecks verlaufen durch diese Schnittpunkte (blau in Abb. 5).

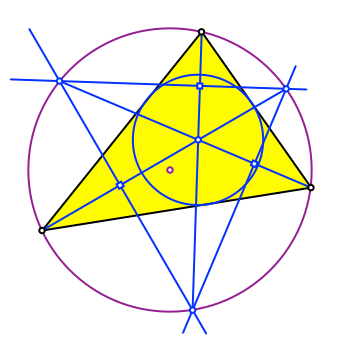
Abb. 5: Winkelhalbierende

Ebenso verlaufen die Mittelsenkrechten der Dreiecksseiten durch diese Schnittpunkte (lila in Abb. 6).

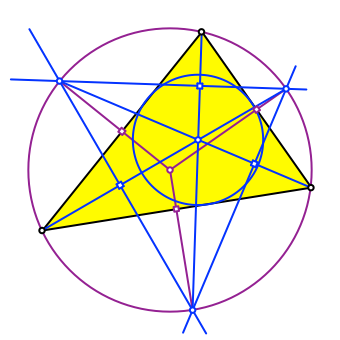
Abb. 6: Mittelsenkrechte

3 Sehnenvierecke

Das rote Viereck in der Abbildung 7 hat zwei gegenüberliegende rechte Winkel und ist daher ein Sehnenviereck mit einem Umkreis.

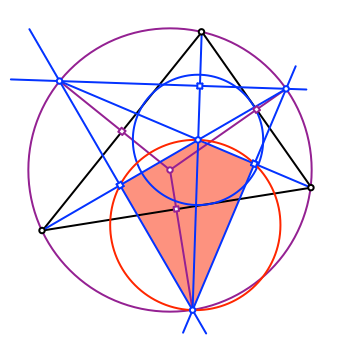
Abb. 7: Sehnenviereck

Es hat insgesamt drei solche Sehnenvierecke (Abb. 8), je mit einem Umkreis (die drei Umkreise sind rot gezeichnet).

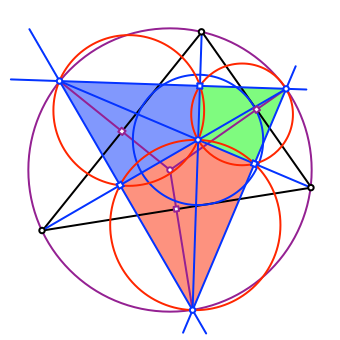
Abb. 8: Drei Sehnenvierecke

Wir lassen die Sehnenvierecke weg und schneiden deren Umkreise mit den Dreiecksseiten (Abb. 9). Dies gibt insgesamt sechs Schnittpunkte.

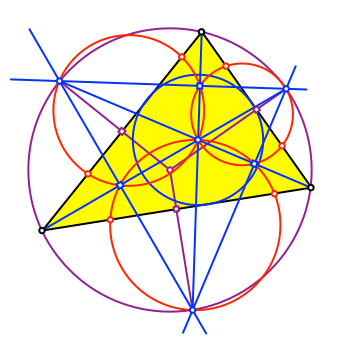
Abb. 9: Sechs Schnittpunkte

4 Sechspunktekreis

Die sechs Schnittpunkte liegen auf einem Kreis (fett schwarz in Abb. 10 und Abb. 11).

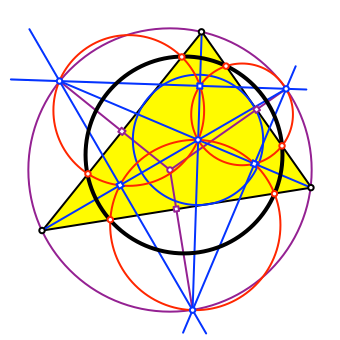
Abb. 10: Sechspunktekreis

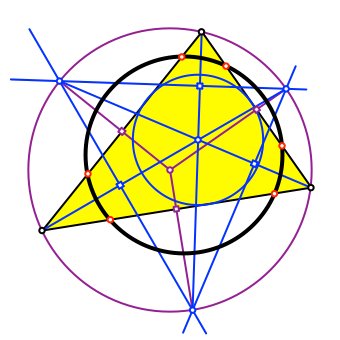
Abb. 11: Sechspunktekreis

5 Weitere Sehnenvierecke

Wir können das Dreieck mit den Mittelsenkrechten in drei weitere Sehnenvierecke zerlegen (Abb. 12). Diese Sehnenvierecke sind verschieden von denen in der Abbildung 8.

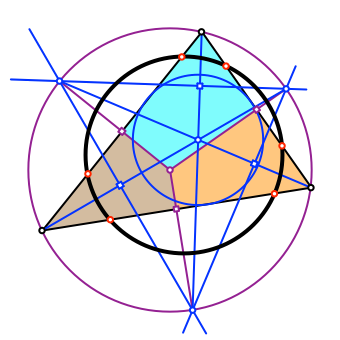
Abb. 12: Drei weitere Sehnenvierecke

Die drei Sehnenvierecke haben ebenfalls je einen Umkreis (Abb. 13).

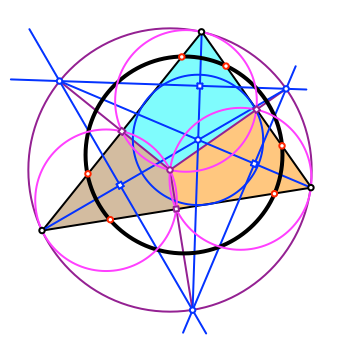
Abb. 13: Umkreise

6 Zwölfpunktekreis

Die sechs Schnittpunkte dieser Umkreise mit den Seiten des blauen Dreiecks liegen ebenfalls auf dem schwarzen Kreis (Abb. 14). Dieser ist also ein Zwölfpunktekreis.

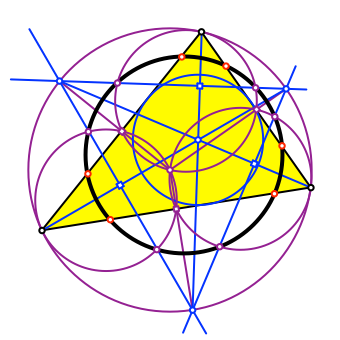
Abb. 14: Zwölfpunktekreis

Die Abbildung 15 zeigt die Umkreise von allen sechs in unserer Konstruktion verwendeten Sehnenvierecke.

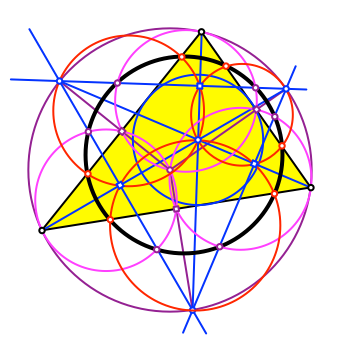
Abb. 15: Sechs Umkreise von Sehnenvierecken

7 Mittelpunkt

Wo liegt der Mittelpunkt (Abb. 16) des schwarzen Kreises?

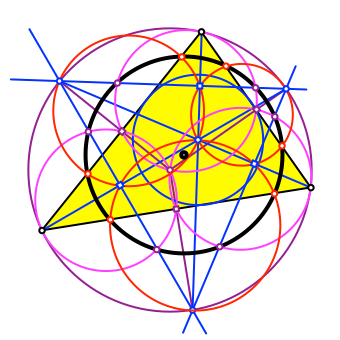
Abb. 16: Mittelpunkt?

Der Mittelpunkt des schwarzen Kreises liegt genau in der Mitte zwischen den Mittelpunkten des Inkreises und des Umkreises (Abb. 17).

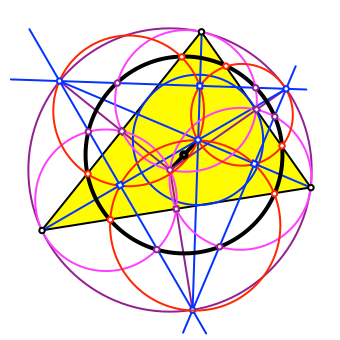
Abb. 17: Mittelpunkt in der Mitte

Links

Thomas Jahre: Aufgabe der Woche

https://www.schulmodell.eu/aufgabe-der-woche.html

Hans Walser: Flächengleichheit

https://walser-h-m.ch/hans/Miniaturen/F/Flaechengleichheit6/Flaechengleichheit6.html