Hans Walser, [20201110]

Inkreis

1 Worum geht es?

Alternative Methode zur Konstruktion des Inkreises eines Dreiecks. Mit DGS durchführbar. Benötigt werden implementierte Makros für Kegelschnitte und für Tangenten.

Fragen der Arbeitsökonomie, der logischen Schlüssigkeit und der Ästhetik.

2 Kommentiertes Vorgehen

In einem Dreieck ABC mit den Seiten a, b, c (mit in unserem Beispiel a < c < b) zeichnen wir die Hyperbel mit den Brennpunkten A und B durch C (Abb. 1.1). Die Software liefert mit dem Button „Hyperbel aus den beiden Brennpunkten und einem Hyperbelpunkt“ beide Hyperbeläste. Wir benötigen nur den durch C verlaufenden Ast h.

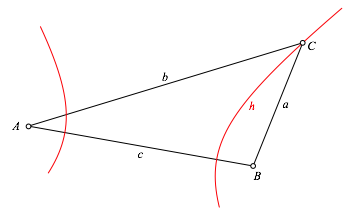
Abb. 1.1: Hyperbel

Wir schneiden den Hyperbelast h mit der Seite AB (Abb. 2). Der Schnittpunkt D ist einer der Scheitelpunkt des Hyperbelastes h. Er ist auch der Berührungspunkt des Inkreises mit der Seite AB. Dies kann wie folgt eingesehen werden: Der Hyperbelast h ist der Ort aller Punkte, deren Abstandsdifferenz zu A beziehungsweise B gleich b – a ist. Somit ist:

(1)

Andererseits ist:

(2)

Daraus ergibt sich:

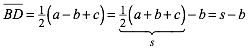(3)

Das ist aber auch der Abstand des Berührungspunktes von der Ecke B.

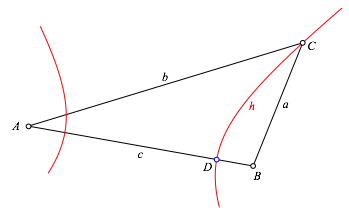
Abb. 1.2: Schnittpunkt D

In D zeichnen wir die Tangente n_c an den Hyperbelast h (Abb. 1.3). Aus Symmetriegründen ist diese Tangente normal zur Dreiecksseite AB. Wir hätten also ebensogut das Lot zu c in D zeichnen können.

Der Mittelpunkt I des gesuchten Inkreises liegt auf n_c.

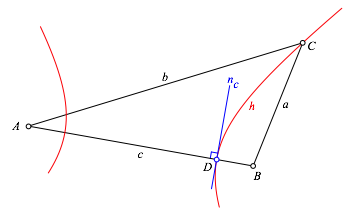
Abb. 1.3: Tangente in D

Nun zeichnen wir in C die Tangente w_C an h (Abb. 1.4). Diese Tangente ist Winkelhalbierende des Dreieckswinkels bei C. Dies folgt daraus, dass bei einem Kegelschnitt mit zwei Brennpunkten die Winkelhalbierenden der Abstandsstrecken von einem Kegelschnittpunkt die Tangente und die Normale zum Kegelschnitt sind.

Der Mittelpunkt I des gesuchten Inkreises liegt auf dieser Winkelhalbierenden.

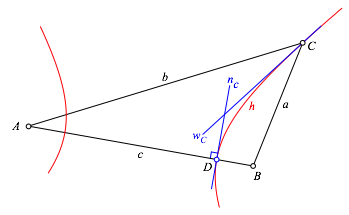
Abb. 1.4: Tangente in C

Der Schnittpunkt I von n_c und w_C ist der Mittelpunkt des Inkreises (Abb. 1.5).

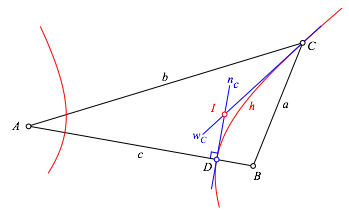
Abb. 1.5: Mittelpunkt des Inkreises

Der gesuchte Inkreis des Dreiecks hat das Zentrum I und verläuft durch D (Abb. 1.6).

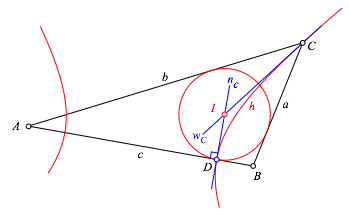
Abb. 1.6: Inkreis

Wir brauchen also sechs Schritte („Handgriffe“) für die Konstruktion des Inkreises. Die Methode ist allerdings stark asymmetrisch, da sie zum Beispiel die drei Eckpunkte oder die drei Seiten des Dreiecks ganz unterschiedlich verwendet.

Analog kann auch ein Ankreis des Dreiecks konstruiert werden. Anstelle der Hyperbel wird mit einer Ellipse gearbeitet (Abb. 2).

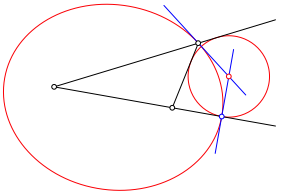
Abb. 2: Ankreis

3 Vergleich mit konventioneller Methode

In der Schule wird der Inkreis traditionellerweise mit den Winkelhalbierenden konstruiert. Man beginnt mit zwei Winkelhalbierenden und deren Schnittpunkt (Abb. 3.1 bis 3.3).

Abb. 3.1: Erste Winkelhalbierende

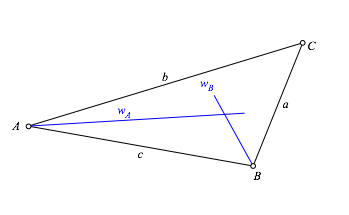
Abb. 3.2: Zweite Winkelhalbierende

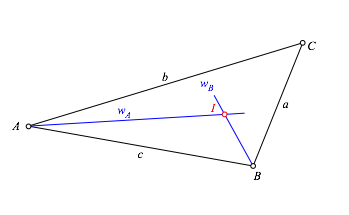
Abb. 3.3: Schnittpunkt der beiden Winkelhalbierenden

Nun wird vom Schnittpunkt aus das Lot auf eine Seite gefällt und der Schnittpunkt mit dieser Seite festgelegt (Abb. 3.4 und 3.5).

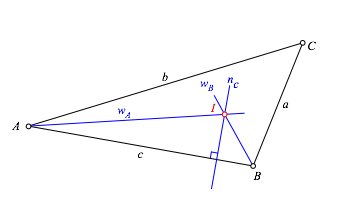
Abb. 3.4: Lot auf eine Seite

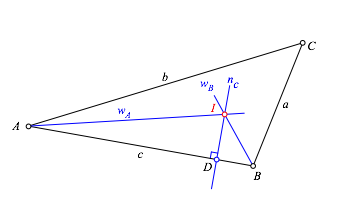
Abb. 3.5: Schnittpunkt

Jetzt kann der Inkreis gezeichnet werden (Abb. 3.6).

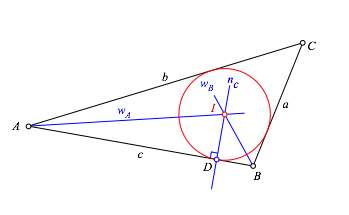
Abb. 3.6: Inkreis

Wir benötigen ebenfalls sechs Schritte zur Konstruktion des Inkreises. Auch diese Methode ist asymmetrisch bezüglich der Berücksichtigung der Dreieckselemente.

Die beiden hier geschilderten Verfahren zur Konstruktion des Inkreises sind also vom Arbeitsaufwand her gesehen gleichwertig wenn auf die Anzahl der Schritte abstellt wird. Beide Methoden sind asymmetrisch bezüglich der Dreieckselemente.

Der Kognitionsaufwand der beiden Methoden ist unterschiedlich. Das Verfahren der Abbildung 1 benötigt zum Verständnis Kenntnisse über Kegelschnitte.

4 Problematik der Ortslinien

Das Verfahren der Abbildung 1 mit der Hyperbel hat bei der Verwendung von dynamischer Geometrie Software eine weitere interessante Tücke. In der Abbildung 1 habe ich mit dem Button „Hyperbel aus Brennpunkten und einem Hyperbelpunkt“ gearbeitet und mir weiter nichts überlegt. Es hat funktioniert.

Nun lernt man aber in der Schule eine Abstandsdefinition für die Hyperbel. In unserem Kontext heißt das:

(4)

Punkte mit der Bedingung (5) können (mit Zirkel und Lineal) wie folgt konstruiert werden.

Wir tragen die Seitenlänge a von C aus auf AC ab (Abb. 4.1). Teilpunkt sei E.

Abb.4.1: Abtragen der Seite a

Nun zeichnen wir einen Kreis k um A durch E (Abb. 4.2).

Dieser Kreis hat den Radius b – a. Er wird manchmal als Leitkreis bezeichnet.

Abb. 4.2: Leitkreis k

Auf dem Leitkreis k wählen wir einen beliebigen Punkt Q und zeichnen den Strahl q von A aus über Q (Abb. 4.3).

Abb. 4.3: Beliebiger Punkt Q

Wir schneiden den Strahl q mit der Mittelsenkrechten m von EB. Der Schnittpunkt sei P (Abb. 4.4).

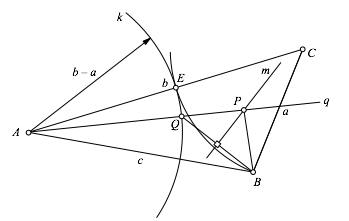
Abb. 4.4: Punkt P

Für P gilt folgendes. Zunächst ist:

(5)

Daraus ergibt sich:

(6)

Der Punkt P liegt wegen (4) auf dem Hyperbelast. Wir erhalten nun diesen Hyperbelast mit dynamischer Geometrie Software als Ortslinie von P bei Variation von Q (Abb. 4.5). Als Zugabe ergibt die Mittelsenrechte m als Hyperbeltangente in P.

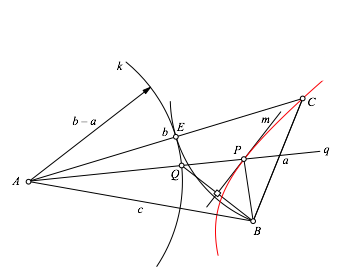
Abb. 4.5: Hyperbelast

Damit sind wir also gleich weit wie in der Abbildung 1.1.

Und nun kommt der große Frust: das System weigert sich, den Schnittpunkt D (Abb. 1.2) oder die Tangente w_C (Abb. 1.4) anzugeben.

Ortslinien sind Sackgassen (Zsákutca). Wir können damit nicht weiterarbeiten. Der Hintergrund liegt wohl darin, dass Ortslinien eine Punkt für Punkt Konstruktion mit Interpolation sind. Dies sieht auf dem Bildschirm gut aus, ist aber nicht exakt. Ortslinien sind also nur Visualisierungen, keine geometrische Elemente.

5 Schadensbegrenzung

Wir können die Ortslinie umgehen, indem wir die relevanten Positionen von Q selber wählen. Also sozusagen händisch. Wenn wir Q₁ auf AB wählen, wird m₁ = n_c (Abb. 5). Wenn wir Q₂ = E wählen, wird m₂ = n_c und wir können den Inkreis zeichnen.

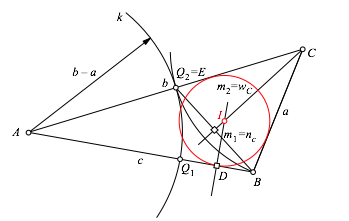
Abb. 5: Arbeiten mit Sonderfällen

Die einzelnen Arbeitsschritte sind:

(1) Kreis um C mit Radius a.

(2) Schnittpunkt E

(3) Leitkreis k

(4) Schnittpunkt Q₁

(5) Mittelsenkrechte m₁

(6) Punkt D

(7) Mittelsenkrechte m₂

(8) Schnittpunkt I

(9) Umkereis

6 Ein schöner Schnittpunkt

Gemeinsame Schnittpunkte von drei Linien werden in der Geometrie immer besonders gefeiert. In der Dreiecksgeometrie kennen wir den Seitenhalbierenden-Schnittpunkt, den Winkelhalbierenden-Schnittpunkt, den Höhen-Schnittpunkt und den Mittelsenkrechten-Schnittpunkt. Neben diesen vier Klassikern gibt es allerdings noch viele weitere Schnittpunkte (Walser 2012).

Der Legende nach war Hans Freudenthal (1905-1990) von solchen Schnittpunkten derart betroffen, dass er sich entschloss, sein Leben der Mathematik und ihrer Didaktik zu widmen.

Abb.6: Hans Freudenthal

Gemeinsame Schnittpunkte von zum Beispiel drei Geraden sind ein beliebtes Tummelfeld für die Anwendung dynamischer Geometrie Software. Meist geht es darum, vermutete Schnittpunkte entweder zu falsifizieren oder aber „empirisch“ zu erhärten. Technisch werden zwei der drei Geraden miteinander geschnitten, und dann wird untersucht, ob der so erhaltene Schnittpunkt auf der dritten Geraden liegt. Dafür gibt es einen eigenen Button. Da allerdings der Test nur numerisch arbeitet, ist er rein geometrisch nicht schlüssig.

Falls der Schnittpunkt verneint wird, können so lange hineinzoomen, bis die drei betrachteten Linien auseinanderdriften und ein Dreieck bilden.

Wenn allerdings der numerische Test ein positives Ergebnis liefert auch dem Zug-Modus standhält, fällt es schwer, an der Existenz des Schnittpunktes zu zweifeln. Schülerinnen und Schülern sind überzeugt von der Stimmigkeit des Schnittpunktes und sind schwer zu motivieren, noch einen „Beweis“ dazu zu suchen.

Die Wahrscheinlichkeit, dass ein logisch korrekter Beweis doch irgendwo einen logischen Fehler oder eine Lücke enthält, dürfte deutlich größer sein als die Wahrscheinlichkeit der Nichtexistenz eines numerisch und mit dem Zug-Modus empirisch erhärteten Schnittpunktes.

Doch zurück zu unseren Hyperbeln.

Wir zeichnen im Dreieck alle drei Hyperbeläste gemäß (vgl. Abb. 1.1) ein. Jede Hyperbel hat zwei der drei Dreiecksecken als Brennpunkte und verläuft durch die jeweilige dritte Ecke (Abb. 7).

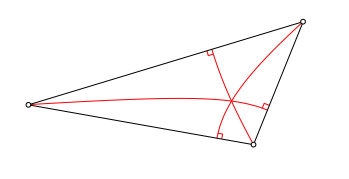
Abb. 7: Drei Hyperbeläste

Die Figur mutet etwas surrealistisch an und ist gewöhnungsbedürftig.

Unabhängig von der Frage nach dem vermuteten Schnittpunkt haben wir nun aber eine weitere Methode zur Konstruktion des Inkreises gefunden (Abb. 8).

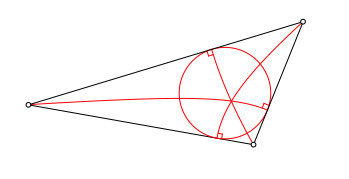
Abb. 8: Inkreis

Die Fußpunkte der drei Hyperbelbögen sind die Berührungspunkte des Inkreises. Wir brauchen also nur noch den Kreis durch diese drei Punkte zu zeichnen.

Diese Methode braucht allerdings sieben Handgriffe statt nur sechs: je drei Mal die Hyperbel und den Schnittpunkt mit der Dreiecksseite. Dann den Kreis durch die drei Schnittpunkte. Dafür ist diese Methode vollständig symmetrisch bei der Berücksichtigung der Dreieckselemente. Vom ästhetischen Standpunkt her ist sie die schönste.

Und nun zur Frage der Existenz des Schnittpunktes der drei Hyperbeläste.

Wenn wir die Hyperbeln mit dem Button „Hyperbel aus Brennpunkten und einem Hyperbelpunkt“ zeichnen, können wir problemlos den Schnittpunkt zweier Hyperbeläste generieren. Der numerische Test, ob dieser Punkt auch auf dem dritten Hyperbelast liegt, verläuft positiv. So weit so gut.

Wenn wir die Hyperbeln nach der Abstandsdefinition mit Hilfe des Leitkreises als Ortslinien generieren, weigert sich das System, einen Schnittpunkt festzulegen.

Existiert der Schnittpunkt also doch nicht?

Interessanterweise ist es nun gerade die bei dynamischer Geometrie Software unbrauchbare Abstandsdefinition, welche einen Beweis gestattet, der wohl auch die Gralshüter der reinen Lehre pädagogisch befriedigt. Wir arbeiten mit den Bezeichnungen der Abbildung 9.

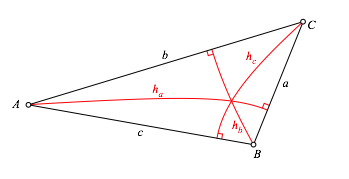
Abb. 9: Bezeichnungen

Es ist:

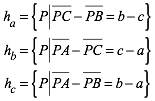(7)

Es sei nun Q der Schnittpunkt von h_a und h_b. Wegen den ersten beiden Zeilen von (7) gilt daher:

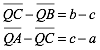(8)

Addition der beiden Zeilen von (8) ergibt:

(9)

Damit liegt Q auch auf h_c. Dies war zu zeigen.

Nachdem der Schnittpunkt also existiert, stellt sich die Frage nach seiner geometrischen Bedeutung. Dazu zeichnen wir das Kreisbogendreieck der Abbildung 10. Jeder Bogen hat eine Dreiecksecke als Zentrum und beginnt und endet bei einem Hyperbelfußpunkt. Der Schnittpunkt der drei Hyperbeläste ist das Zentrum des Inkreises dieses Kreisbogendreieckes. Der Beweis arbeitet mit der Abstandseigenschaft der Hyperbeln.

Die Konstruktion dieses Inkreises ist ein Sonderfall des Problems des Apollonios.

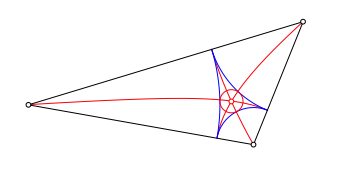
Abb. 10: Kreisbogendreieck

7 Historisches

Die Überlegungen mit den Kegelschnitten im Dreieck gehen auf den flämischen Mathematiker und Mediziner Adriaan van Roomen (1561-1615) zurück. Er löste das an sich mit Zirkel und Lineal lösbare Problem des Apollonius (zu drei gegebenen Kreisen einen vierten berührenden Kreis zu finden) mit Hilfe von Kegelschnitten.

Literatur

Walser, Hans (2012): 99 Schnittpunkte. Beispiele – Bilder – Beweise. 2. Auflage. EAGLE, Edition am Gutenbergplatz: Leipzig. ISBN 978-3-937219-95-0.

Weblink

Hans Walser: Der Inkreis. Vortrag

http://www.walser-h-m.ch/hans/Vortraege/20170209/index.html

Hans Walser: Inkreise von Bogendreiecken

http://www.walser-h-m.ch/hans/Miniaturen/I/Inkreise_Bogendreiecke/Inkreise_Bogendreiecke.htm