Hans Walser, [20110116b]
Ein hyperbolisches Zwšlfeck
In der hyperbolischen
Geometrie zeichnen wir das halbregulŠre Parkett [3,12,3,12], welches aus
regelmŠ§igen Dreiecken und Zwšlfecken besteht und zwar so, dass an jeder Ecke
zwei Dreiecke und zwei Zwšlfecke Ÿber Eck zusammensto§en.
Die Abbildung skizziert
einen Ausschnitt davon im Kreismodell von PoincarŽ. Es sind sechs Zwšlfecke
vollstŠndig gezeichnet.
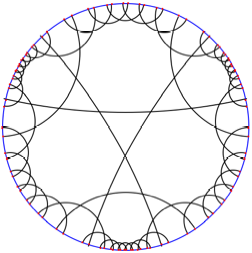
Zwšlfecke und Dreiecke
Nun zeichnen wir
exemplarisch in einem Zwšlfeck drei Diagonalen vom Typ 
ein. Das sind
Diagonalen, welche jeweils vier Ecken des Zwšlfecks Ÿberspringen und dann bei
der fŸnften Ecke wieder landen.
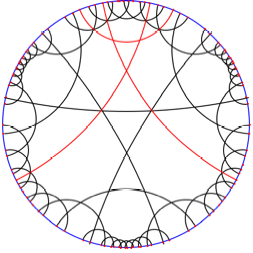
Drei Diagonalen
Diese drei Diagonalen
bilden vier gleichseitige Dreiecke, welche zu den Rasterdreiecken kongruent
sind (Verifikation CAS / DGS). Die Diagonalen sind also drei Mal so lang wie
die Seiten. Das ist erstaunlich.
Im ebenen Fall ist das
mittlere Dreieck grš§er.
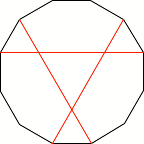
Ebene Situation
In der folgenden
Abbildung sind in sechs Zwšlfecken alle Diagonalen dieses Typs eingezeichnet.
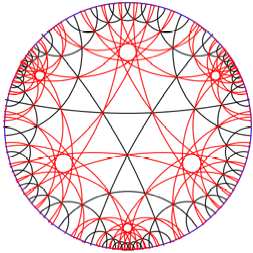
Viele Diagonalen
In einem Streifenmodell
(Einbettung in den euklidischen Raum) kšnnen also fŸr die Rasterlinien und die
Diagonalen Streifen mit derselben €quidistanz verwendet werden. Die Abbildung
zeigt ein Modell mit einem Zwšlfeck und den Diagonalen. Die FlŠche krŸmmt sich
stark, so dass das grŸne Zwšlfeck kaum erkennbar ist.
Streifenmodell