Hans Walser, [20220513]

Hüllkreis

Idee und Anregung: Thomas Jahre: Aufgabe 60 – 712

1 Worum geht es?

Zu n gegebenen Punkten wird der kleinste Kreis gesucht, der diese Punkte im Innern oder auf dem Rand enthält. Ein Minimax-Problem.

2 Vorgehen

Wir studieren zunächst den Fall n = 3 und anschließend den allgemeinen Fall.

2.1 Drei Punkte

Wir verbinden die drei Punkte zu einem Dreieck.

Nun treffen wir folgende Fallunterscheidung:

(i) Das Dreieck ist spitzwinklig. Der Hüllkreis ist der Umkreis des Dreieckes (Abb. 1).

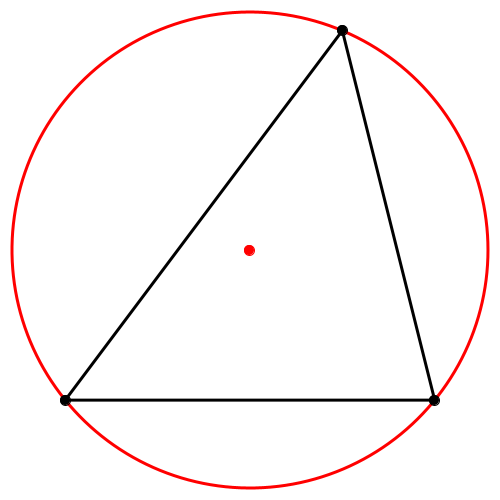
Abb. 1: Spitzwinkliges Dreieck

(ii) Das Dreieck ist rechtwinklig. Der Hüllkreis ist der Thaleskreis des rechtwinkligen Dreiecks (Abb. 2). Das ist wie im spitzwinkligen Fall der Umkreis des Dreiecks

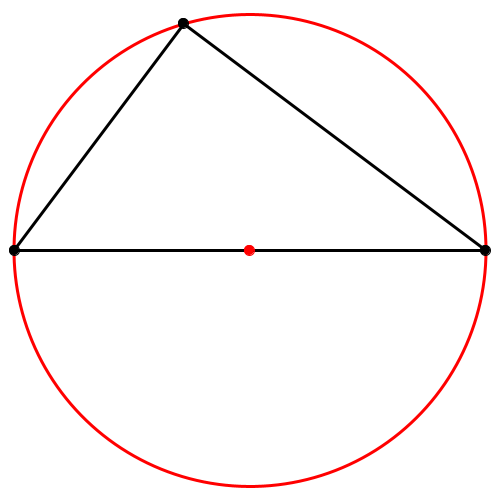
Abb. 2: Rechtwinkliges Dreieck

(iii) Das Dreieck ist stumpfwinklig. Der Hüllkreis ist der Thaleskreis über der längsten Dreiecksseite (Abb. 3). Das ist nicht mehr der Umkreis. Die Ecke mit dem stumpfen Winkel liegt innerhalb des Hüllkreises. Der Umkreis ist größer als der Hüllkreis.

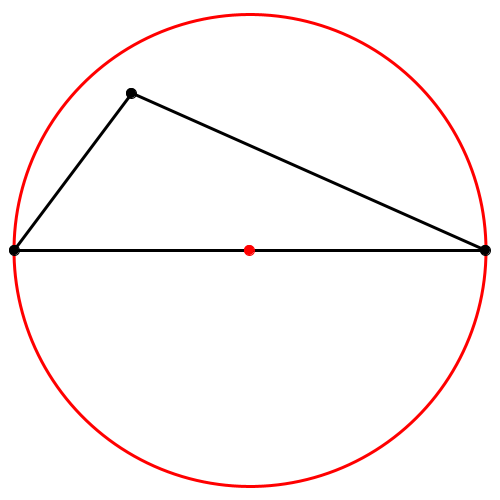
Abb. 3: Stumpfwinkliges Dreieck

Die Abbildung 4 zeigt zunächst ein stumpfwinkliges Dreieck, dann ein rechtwinkliges Übergangsdreieck, dann ein spitzwinkliges Dreieck, dann nochmals ein rechtwinkliges Übergangsdreieck und schließlich wieder ein stumpfwinkliges Dreieck.

Abb. 4: Übergänge

2.2 Mehr als drei Punkte

Bei n > 3 Punkten gibt es

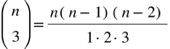
Möglichkeiten, ein (ungeordnetes) Tripel von drei Punkten auszuwählen. Zu jedem Tripel bestimmen wir den Hüllkreisradius und wählen dann dasjenige Tripel mit dem größten Hüllkreisradius (daher der Max vom Minimax). Der zugehörige Hüllkreis ist dann auch der Hüllkreis der gesamten Punktmenge.

3 Beispiele

3.1 Fünf Punkte

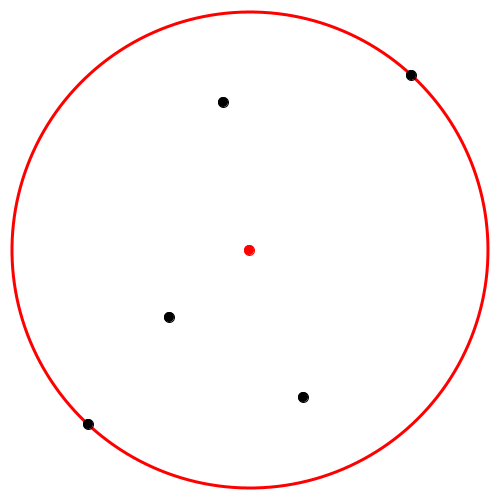
Abb. 5: Fünf Punkte in allgemeiner Lage. Zwei davon auf dem Hüllkreis

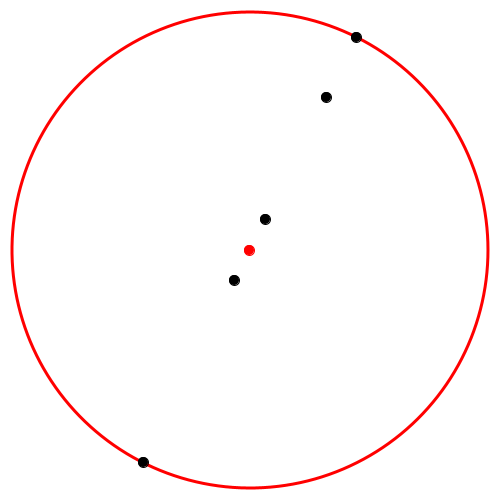
Abb. 6: In Linie

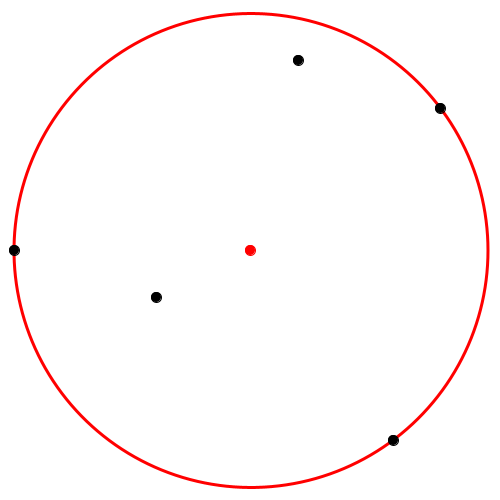
Abb. 7: Drei Punkte auf dem Hüllkreis

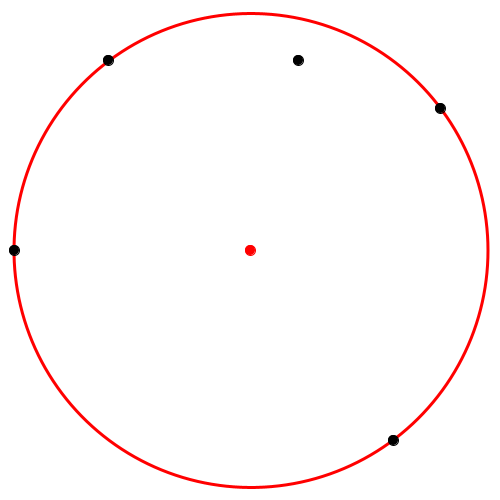
Abb. 8: Vier Punkte auf dem Hüllkreis

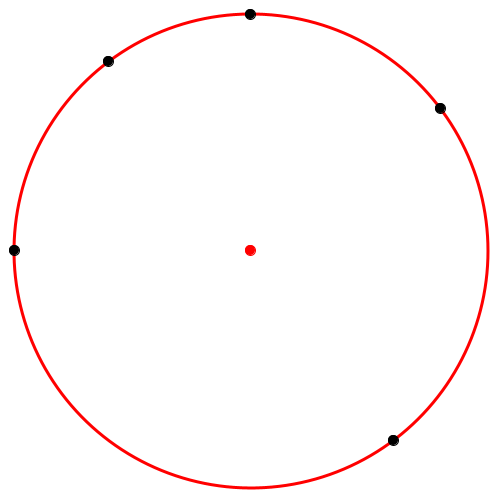
Abb. 9: Alle Punkte auf dem Hüllkreis

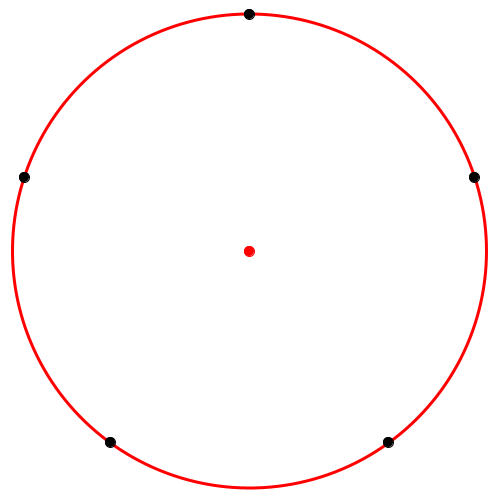
Abb. 10: Regelmäßige Verteilung

3.2 Pythagoras-Ikone

3.2.1 Pythagoreische Dreiecke

Die Abbildung 11 zeigt die 9 Punkte der Pythagoras-Ikone für das rechtwinklige Dreieck mit den Seiten 3, 4 und 5 („Lehrerdreieck“, ägyptisches pythagoreisches Dreieck). Es liegen nur drei der neun Punkte auf dem Hüllkreis. Der Hüllkreisradius ist:

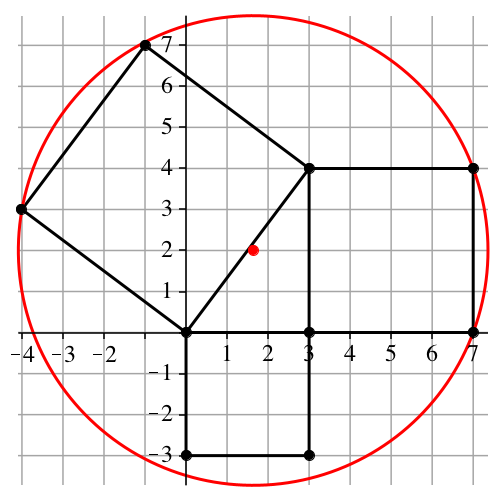
Abb. 11: Ägyptisches Dreieck

Auch beim indischen pythagoreischen Dreieck mit den Seiten 5,12 und 13 liegen nur drei Punkte auf dem Hüllkreis (Abb. 12).

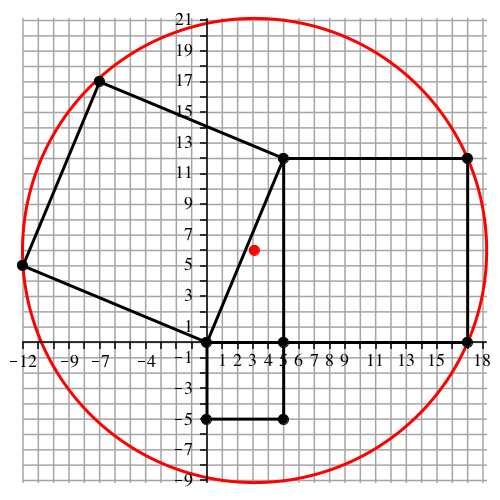
Abb. 12: Indisches Dreieck

3.2.2 Rechtwinklig gleichschenkliges Dreieck

Beim rechtwinklig-gleichschenkligen Dreieck liegen alle sechs Außenpunkt auf dem Hüllkreis (Abb. 13). Der Hüllkreisradius ist:

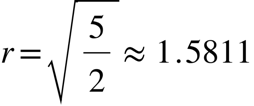
Der Hüllkreis hat dasselbe Zentrum wie der Thaleskreis des Dreieckes.

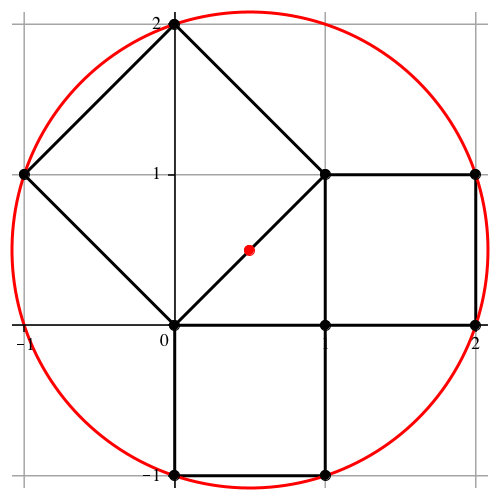
Abb. 13: Rechtwinklig-gleichschenkliges Dreieck

Und schließlich: Die in der Abbildung 14 rot und blau eingezeichneten Strecken stehen im Verhältnis des goldenen Schnittes, und zwar in der Reihenfolge Minor - Major - Minor.

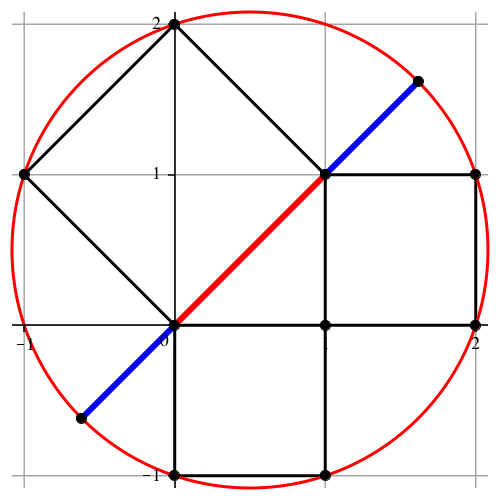
Abb. 14: Minor - Major - Minor

Weblink

Thomas Jahre: Aufgabe der Woche

https://www.schulmodell.eu/aufgabe-der-woche.html

Literatur

Walser, H. (2013a): Der Goldene Schnitt. 6., bearbeitete und erweiterte Auflage. Mit einem Beitrag von Hans Wußing über populärwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.