Hans Walser, [20170828], [20181120]
Halbregulrer Pflasterstein
Anregungen: Heinz Klaus Strick, Leverkusen; Boris Odehnal, Wien
1 Worum geht es?
Mit dem regelm§igen Fnfeck lsst sich die Ebene nicht pflastern, wohl aber mit einem daraus abgeleiteten halbregulren Fnfeck. Analog fr das Siebeneck.
2 Der Pflasterstein
Mit dem regelm§igen Fnfeck lsst sich die Ebene nicht pflastern. Es bleiben nicht schlie§bare Lcken (Abb. 1).
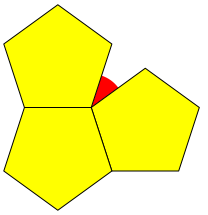
Abb. 1: Lcke
Wir modifizieren unseren Pflasterstein. Wir beginnen mit einem regelm§igen Fnfeck (Abb. 2a) und klappen eine Ecke ein (Abb. 2b). Die Restfigur ist der Umriss unseres Pflastersteins. Er ist gleichseitig, aber nicht gleichwinklig. Daher die Bezeichnung halbregulr. Weiteres zu dieser Figur siehe [1] .
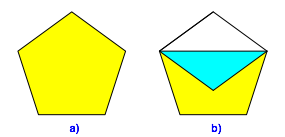
Abb. 2: Verkleinertes Fnfeck
Nun verzieren wir den Pflasterstein mit Teilen von Kreisringen. Die Geometrie dieser Kreisringteile ergibt sich aus der Abbildung 3a. Der Hintergrund ist der Goldene Schnitt (Walser 2013).
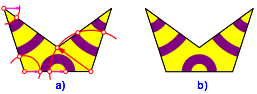
Abb. 3: Teile von Kreisringen
Die Abbildung 3b zeigt den in den folgenden Figuren verwendeten Pflasterstein.
3 Bandornamente
In der Abbildung 4 sehen wir ein Bandornament mit Schubspiegelsymmetrie.

Abb. 4: Bandornament mit Schubspiegelsymmetrie
In der Abbildung 5 glauben wir einen Mander zu erkennen. Ist es aber ein Mander?

Abb. 5: Mander?
Man beachte, dass wir keine Symmetrieachsen haben. Man beachte weiter, dass wir auch ein einem realweltlichen Mander wegen der Flie§richtung des Wassers keine Symmetrieachsen haben.
4 Parkette
Im Folgenden einige Beispiele von Parketten.

Abb. 6: Simples Parkett

Abb. 7: Parkett 2

Abb. 8: Parkett 3

Abb. 9: Parkett 4

Abb. 10: Parkett 5
5 Rosette
Die Figur der Abbildung 11 hat eine zehnteilige Rotationssymmetrie. Sie lsst sich beliebig weit in die Ebene fortsetzen.

Abb. 11: Rosette
6 Spiralen

Abb. 12: Archimedische Spirale

Abb. 13: Doppelspirale

Abb. 14: Zehnfachspirale
7 Siebeneck
Wir knnen analog mit einem regelm§igen Vieleck ungerader Eckenzahl verfahren. Dia Abbildung 15 zeigt die Situation fr ein regelm§iges Siebeneck. Die Verzierung im halbregulren Siebeneck gestattet gewissen Freiheiten.
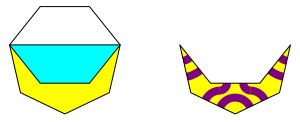
Abb. 15: Halbregulres Siebeneck
Die Abbildung 16 zeigt ein einfaches Bandornament aus halbregulren Siebenecken.

Abb. 16: Bandornament aus halbregulren Siebenecken
Die Abbildung 17 zeigt ein aus dem Bandornament abgeleitetes Flchenornament.

Abb. 17: Flchenornament
Die Abbildung 18 zeigt eine Rosette. Diese kann beliebig weit in die Ebene fortgesetzt werden.

Abb. 18: Rosette
Die Abbildung 19 ist eine Art Doppelrosette. Man kann auch von einer ovalen Anordnung reden.

Abb. 19: Doppelrosette
Die Abbildung 20 zeigt eine archimedische Spirale.

Abb. 20: Archimedische Spirale
Die Abbildung 21 zeigt eine doppelte archimedische Spirale.

Abb. 21: Doppelte archimedische Spirale
Die Abbildung 22 zeigt eine Variante der doppelten archimedischen Spirale.
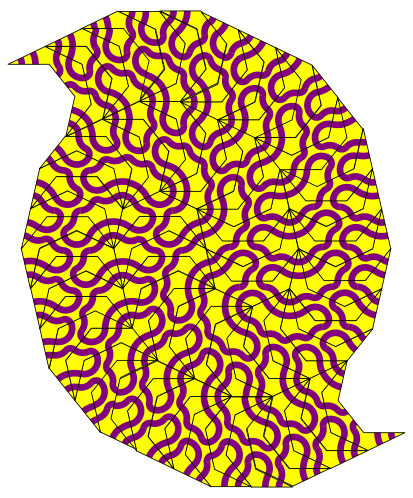
Abb. 22: Doppelte archimedische Spirale. Variante
Es ist mir nicht gelungen, eine 14-fache archimedische Spirale (analog zur Abbildung 14) zu zeichnen. Der ãAnsatzÒ an die zentrale Rosette gelingt nicht.
Literatur
Walser, Hans (6. Auflage). (2013). Der Goldene Schnitt. Mit einem Beitrag von Hans Wu§ing ber populrwissenschaftliche Mathematikliteratur aus Leipzig. Leipzig: Edition am Gutenbergplatz. ISBN 978-3-937219-85-1.
Websites
[1] Hans Walser: Halbregulr (abgerufen 29.8.2017):