Hans Walser, [20220815]

Großes Kuboktaeder

1 Kantenmitten im Würfel

Wir arbeiten mit den zwölf Kantenmittelpunkten im Würfel (Abb. 1).

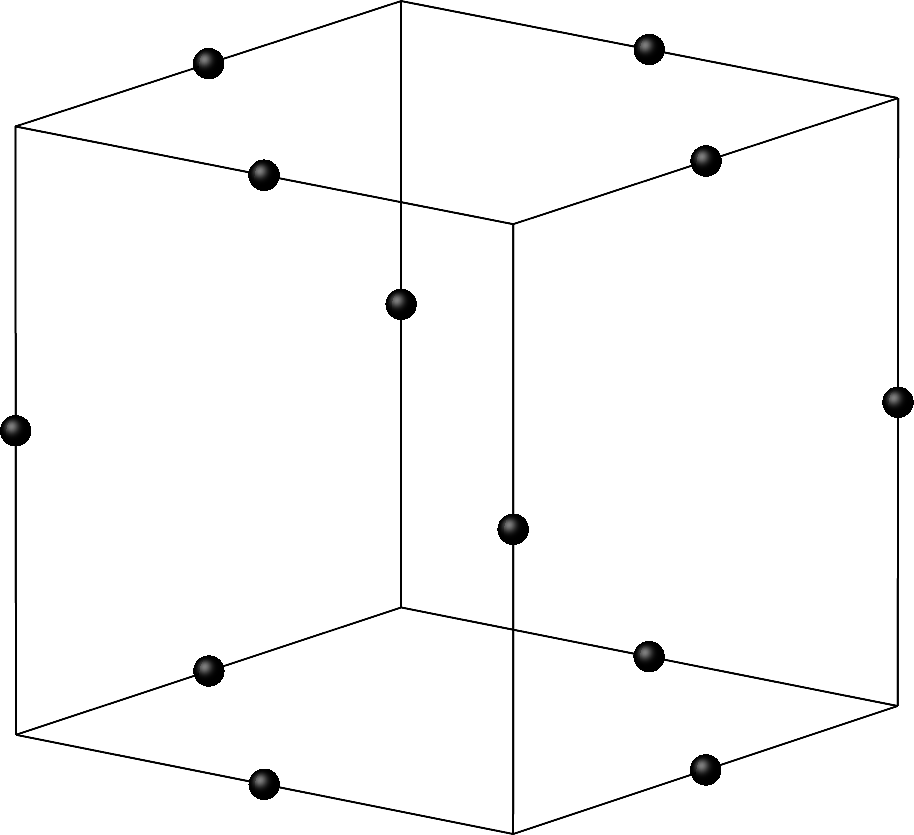
Abb. 1: Kantenmitten im Würfel

2 Das gewöhnliche Kuboktaeder

Wir können „benachbarte“ Punkte zu einem gleichseitigen Dreieck verbinden (Abb. 2). Die drei Trägerkanten der benachbarten Punkte schneiden sich in einer Würfelecke.

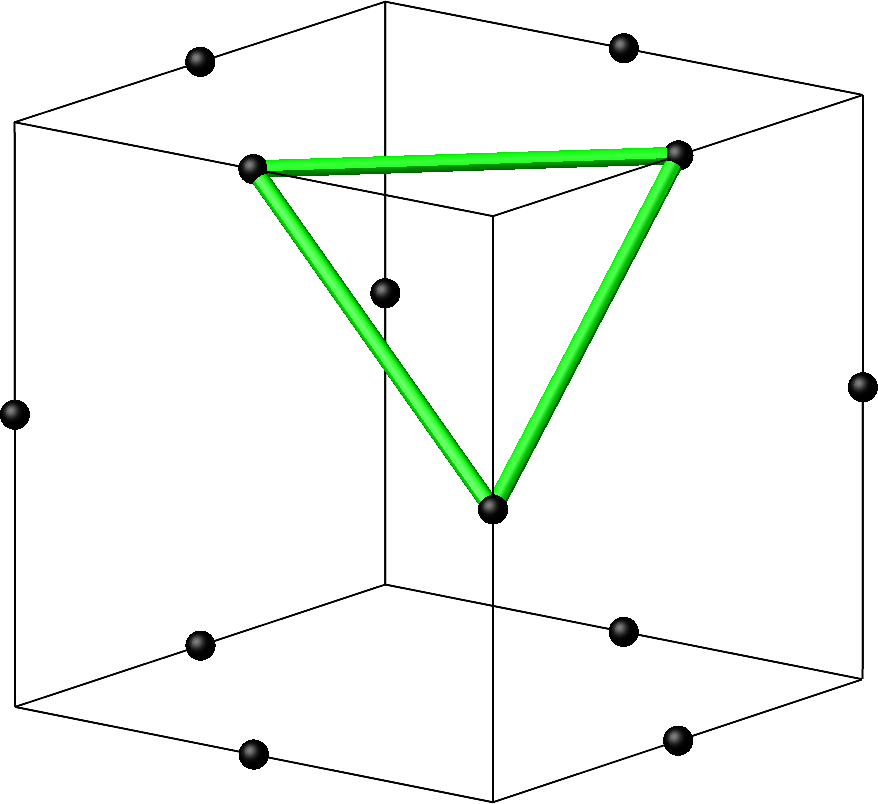
Abb. 2: Gleichseitiges Dreieck

Wenn wir mit sämtlichen Punkten so verfahren, entsteht das Kantengerüst des Kuboktaeders (Abb. 3 und 4).

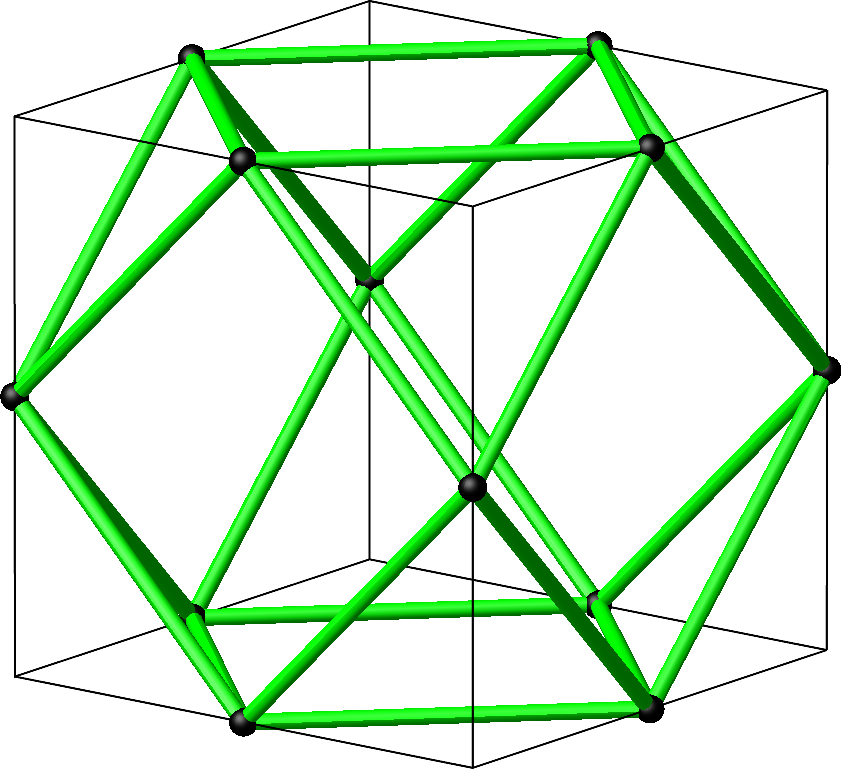
Abb. 3: Kuboktaeder

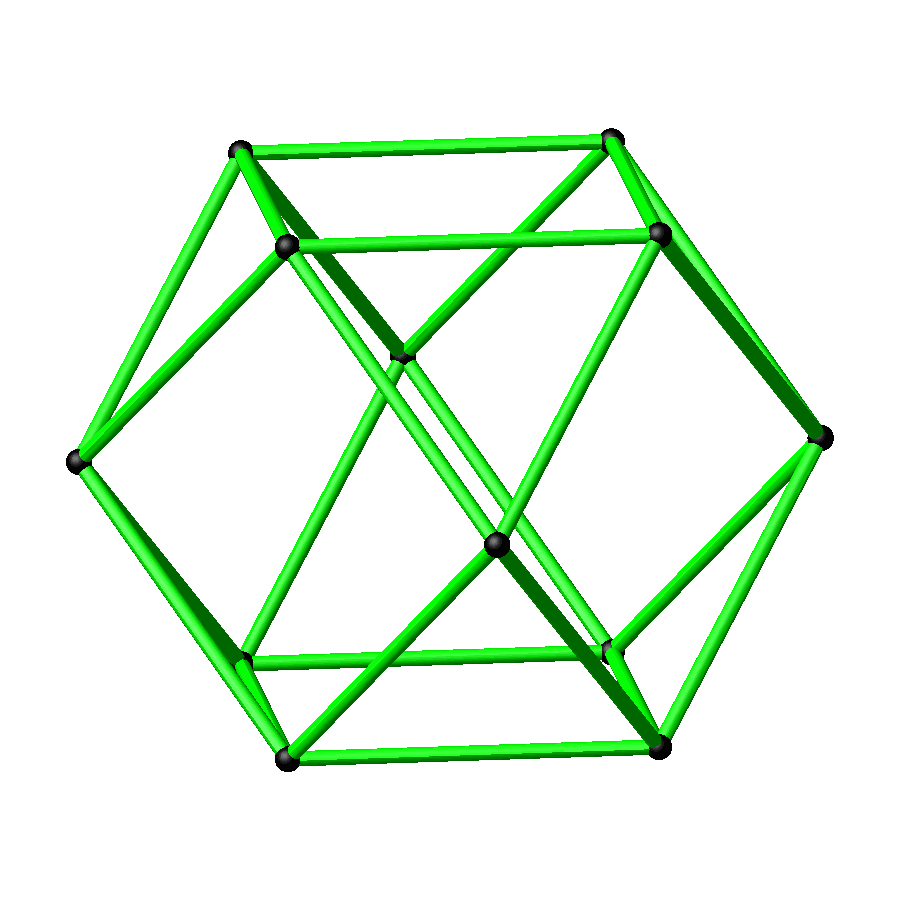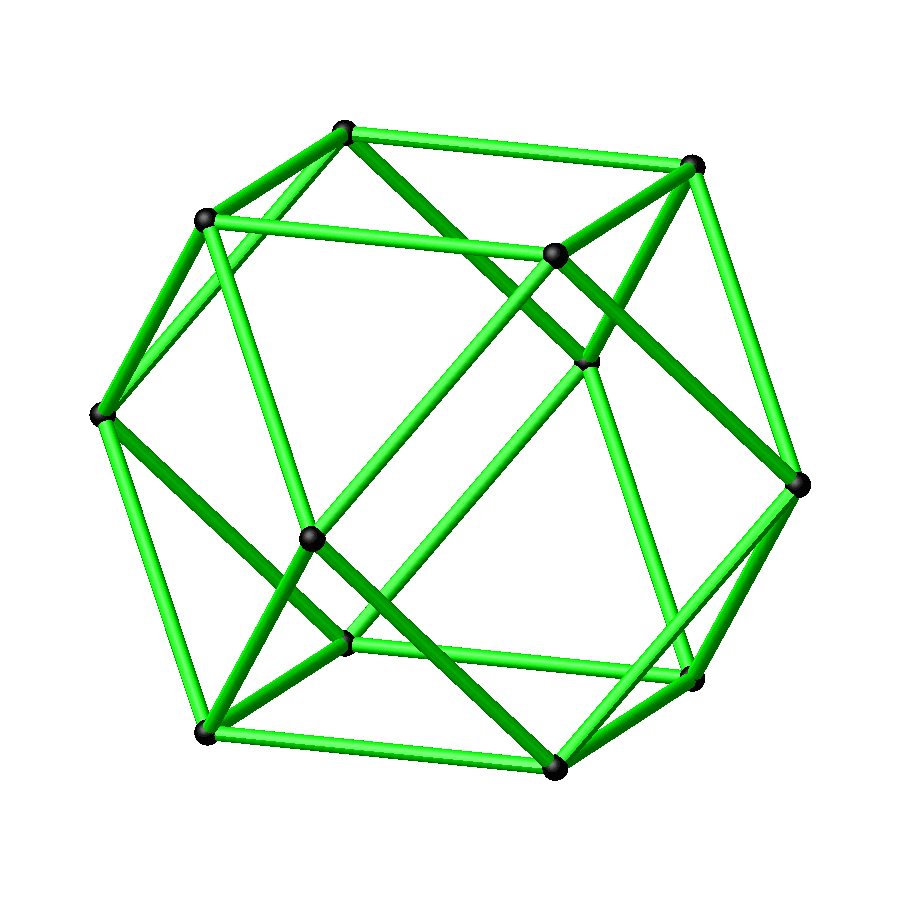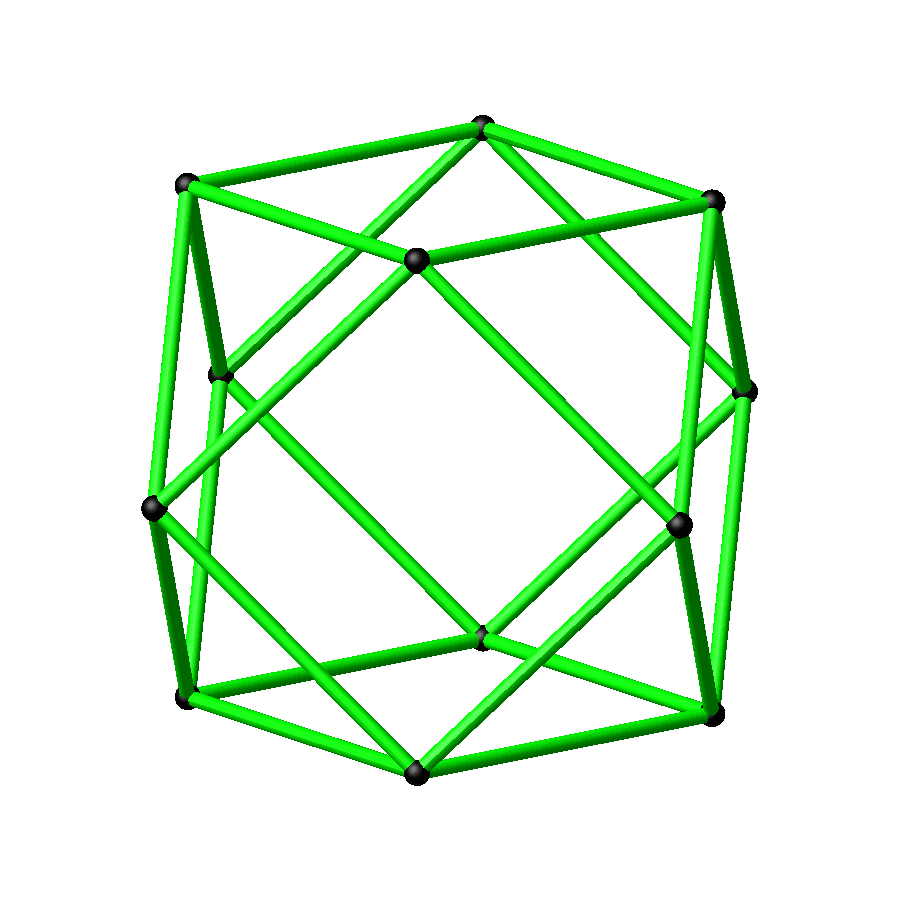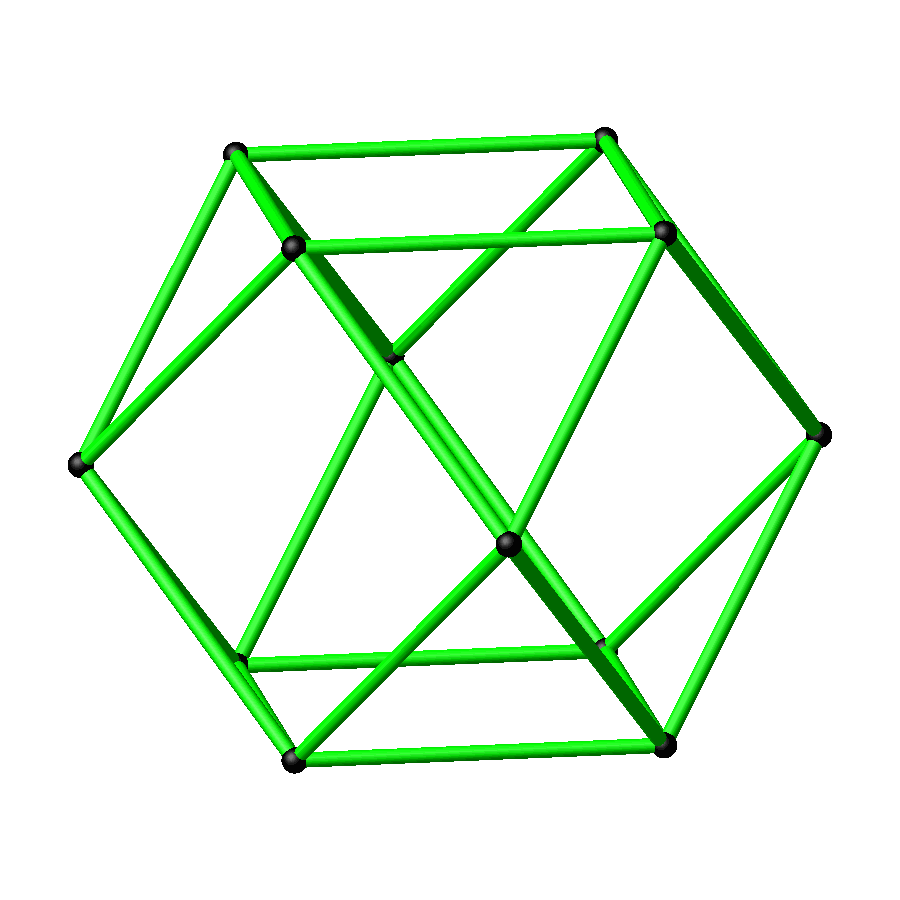
Abb. 4: Rotierendes Kuboktaeder

Die Oberfläche des Kuboktaeders besteht aus acht gleichseitigen Dreiecken und sechs Quadraten (Abb. 5).

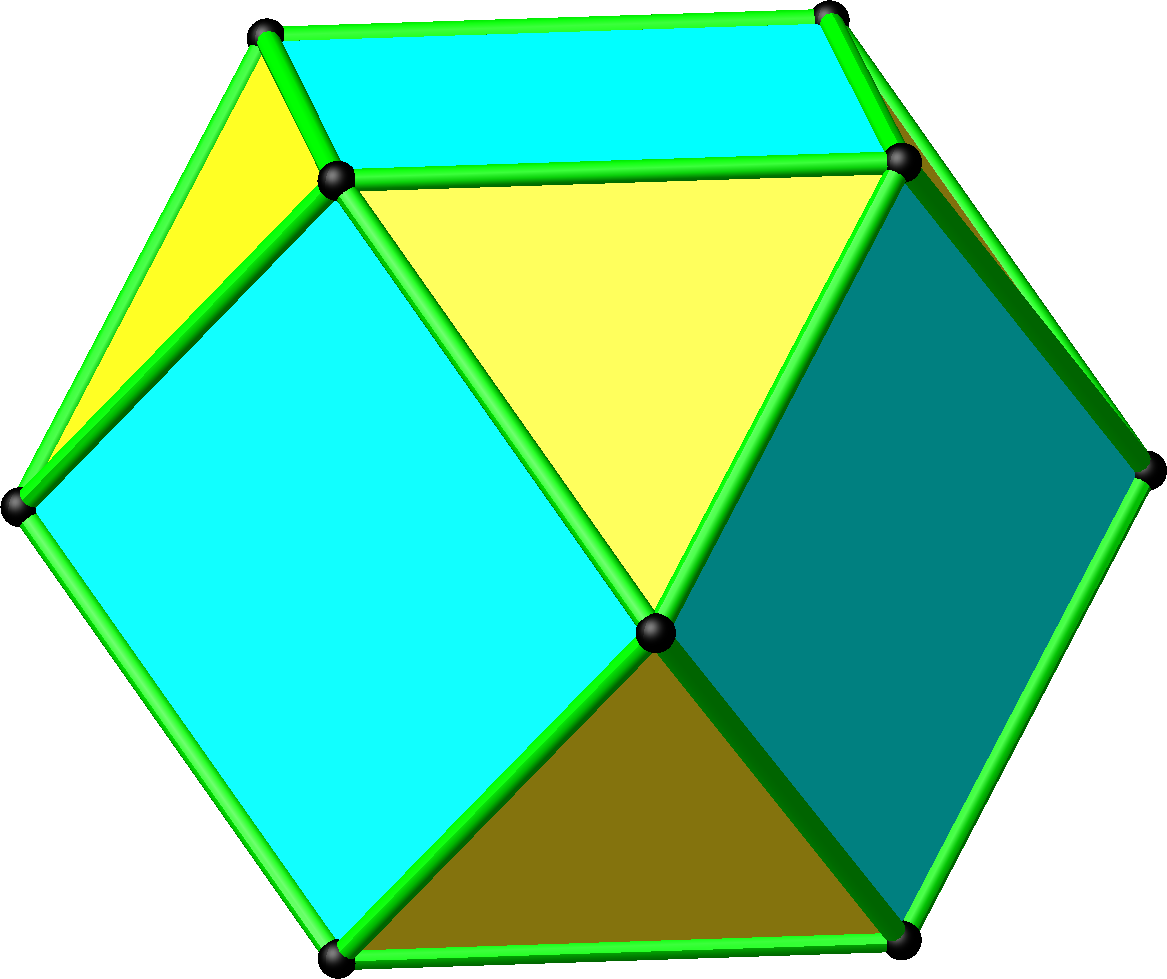
Abb. 5: Oberfläche des Kuboktaeders

3 Das große Kuboktaeder

Drei ausgewählte Punkte der Kantenmitten des Würfels (Abb. 1) lassen sich auch zu einem großen gleichseitigen Dreieck verbinden (Abb. 6). Die drei Trägerkanten der beteiligten Kantenmitten sind windschief. Die Seitenlänge des großen gleichseitigen Dreiecke ist √3-mal so groß wie jene des Dreieckes der Abbildung 2.

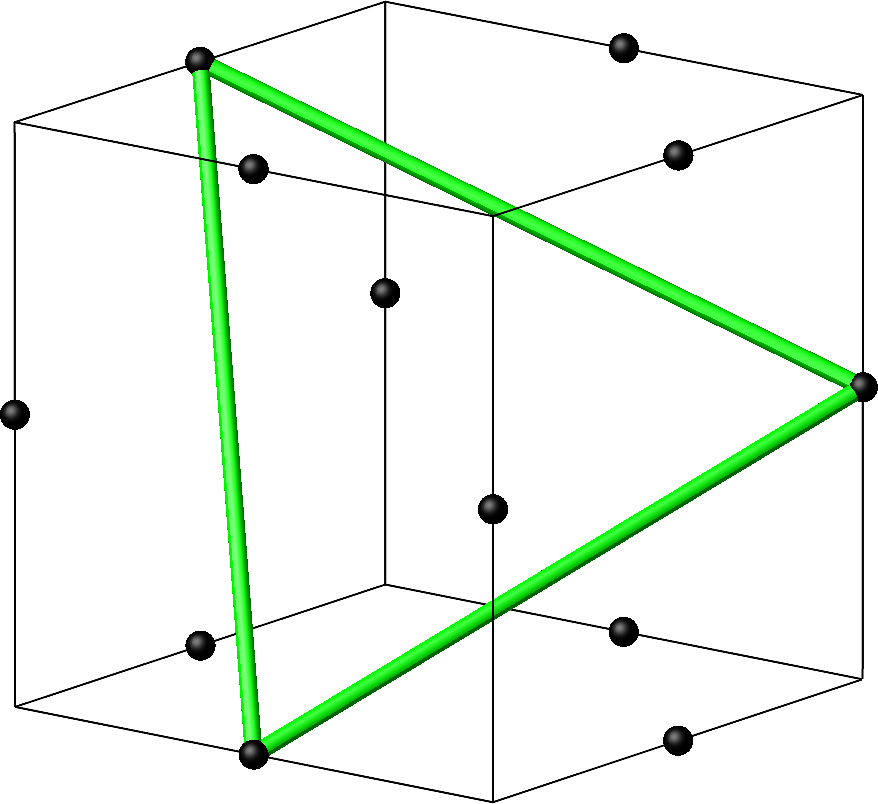
Abb. 6: Großes gleichseitiges Dreieck

Wenn wir mit sämtlichen Punkten so verfahren, entsteht das Kantengerüst des großen Kuboktaeders (Abb. 7 und 8). Die Kanten schneiden einander in den Mittelpunkten und in den Drittelpunkten.

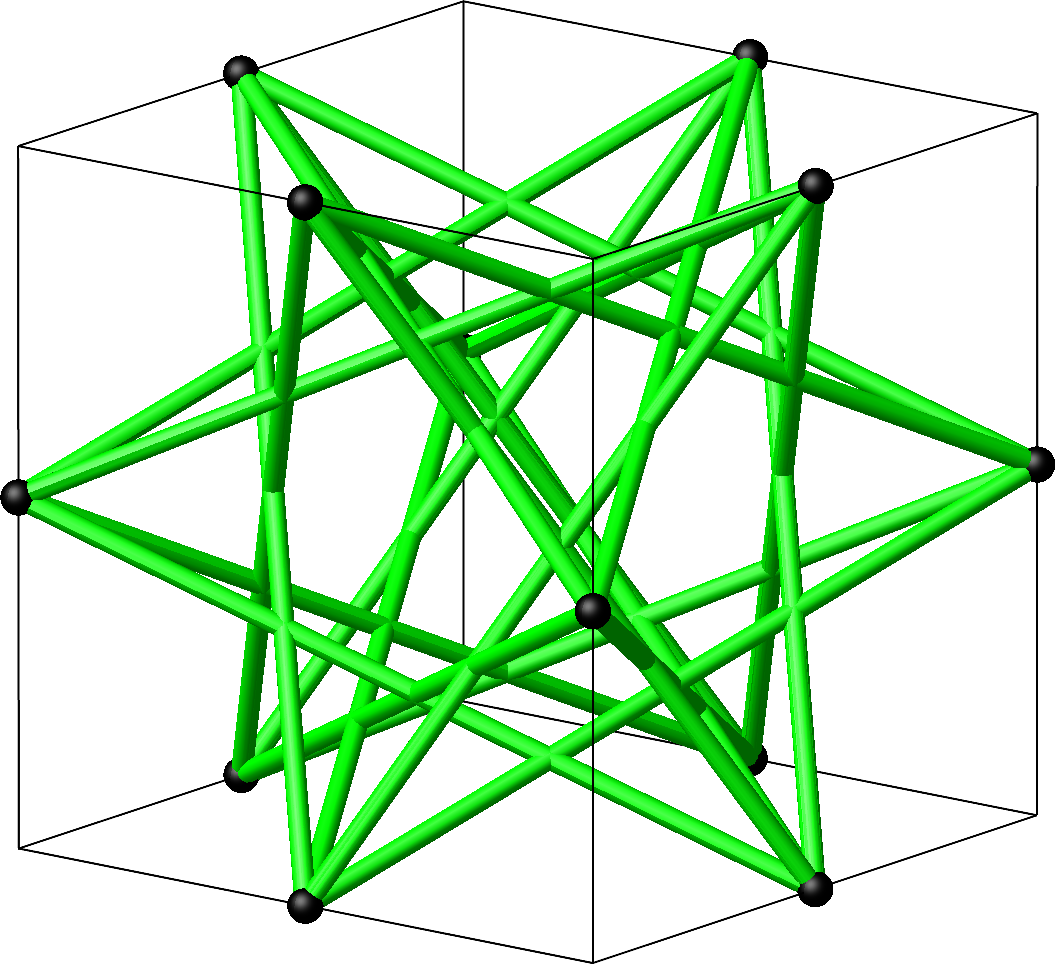
Abb. 7: Großes Kuboktaeder

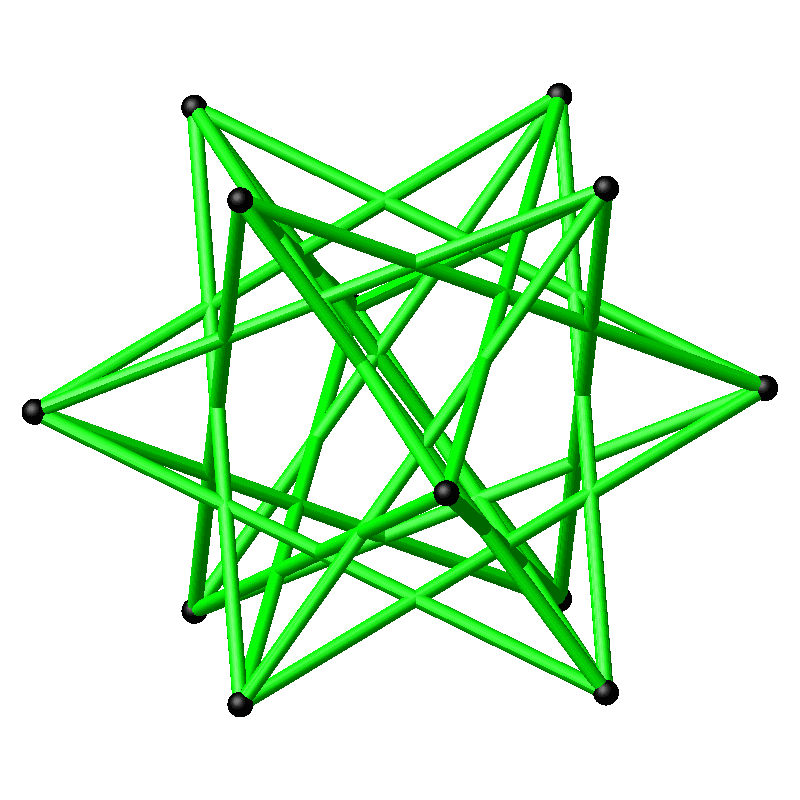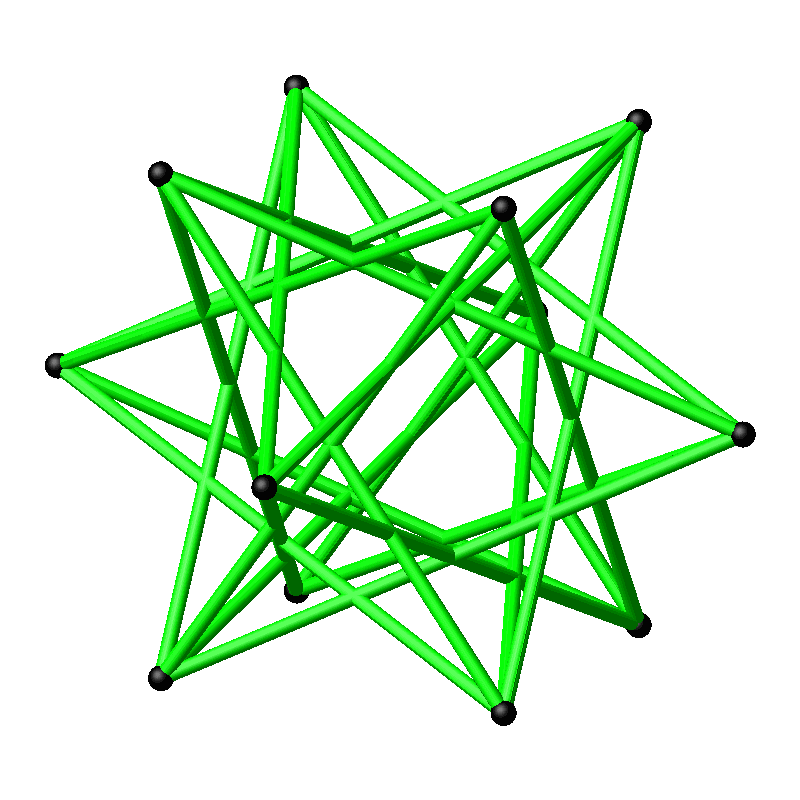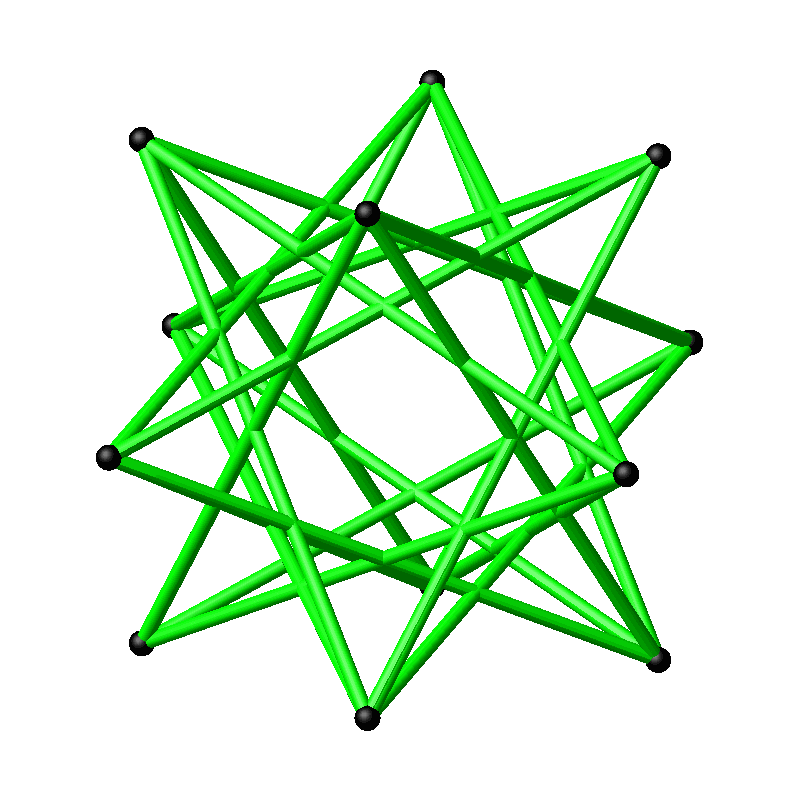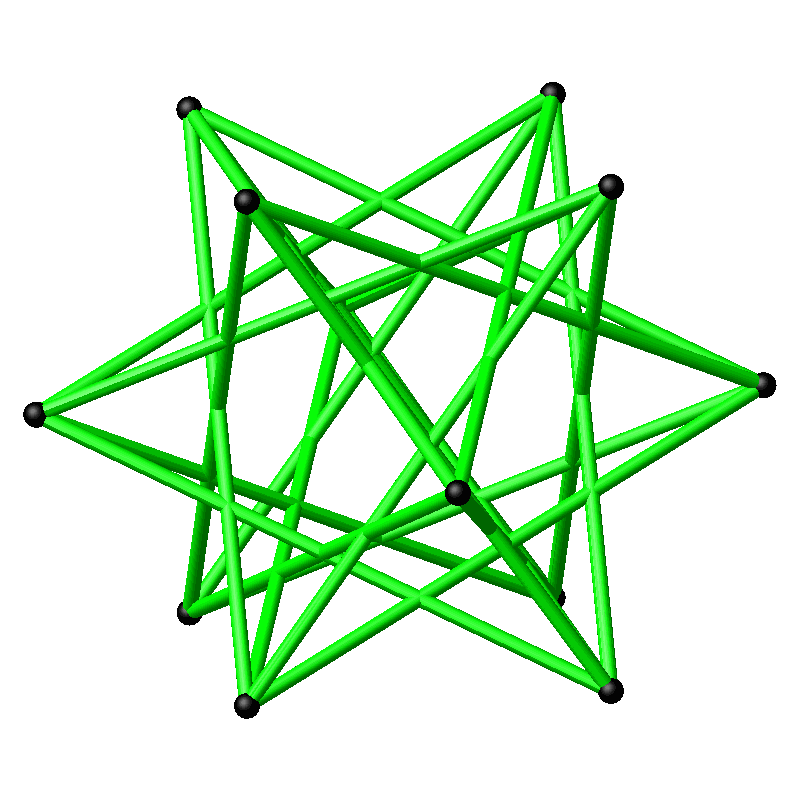
Abb. 8: Rotierendes großes Kuboktaeder

4 Oberfläche

Mit der Oberfläche ist es nun so eine Sache.

4.1 Dreiecke

Die großen gleichseitigen Dreiecke enthalten den Würfelmittelpunkt (Abb. 9).

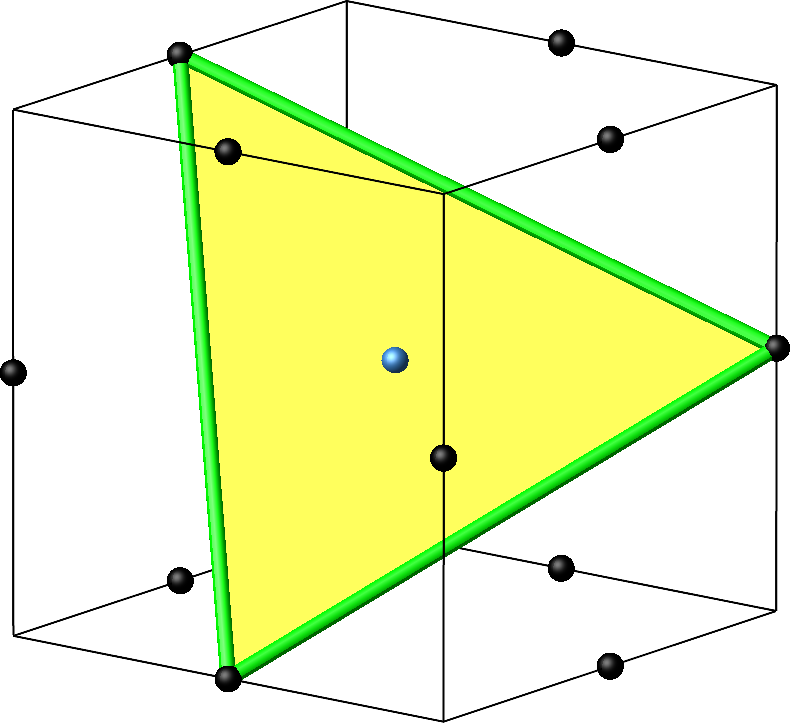
Abb. 9: Würfelmittelpunkt

Dies hat zur Folge, dass die den beiden im gewöhnlichen Kuboktaeder gegenüberliegenden parallelen Dreiecke aufeinanderfallen und einen Davidstern bilden (Abb. 10).

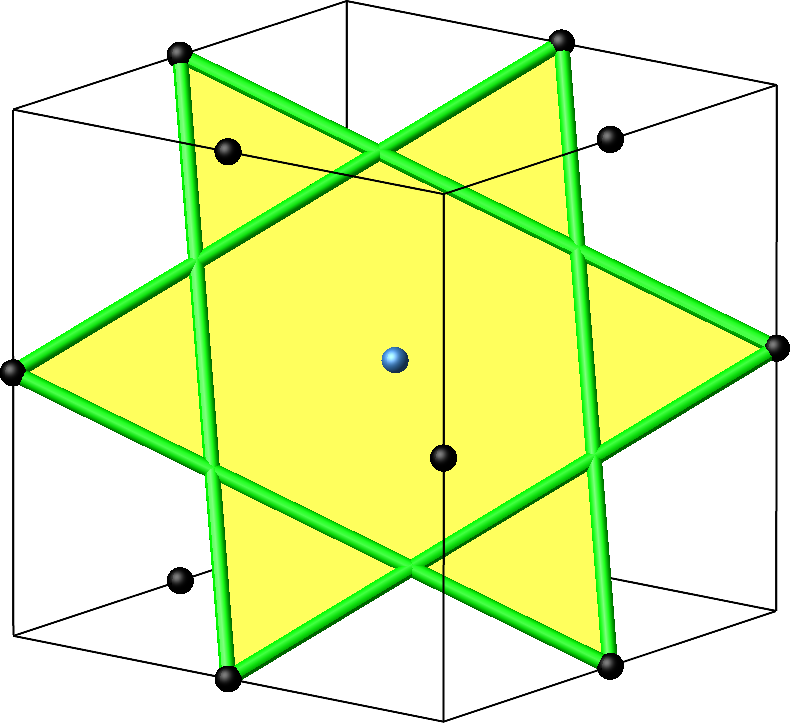
Abb. 10: Davidstern

Statt acht einzelner gleichseitiger Dreiecke wie beim gewöhnlichen Kuboktaeder haben wir im großen Kuboktaeder vier Davidsterne (Abb. 11 und 12).

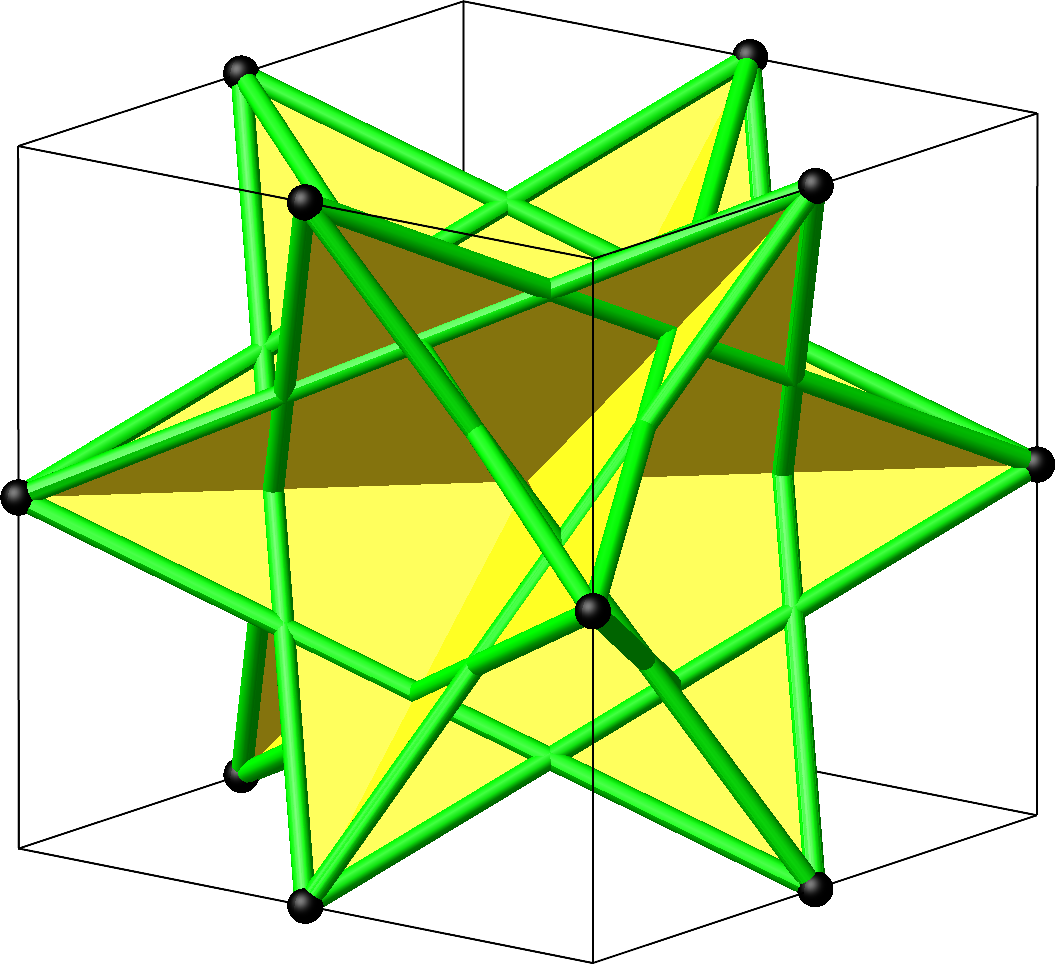
Abb. 11: Vier Davidsterne

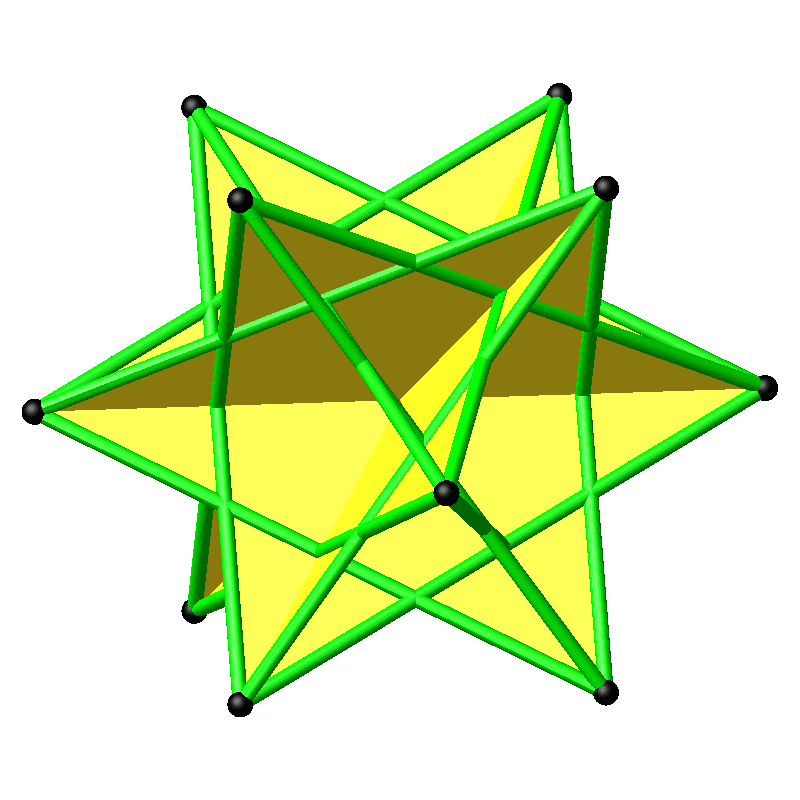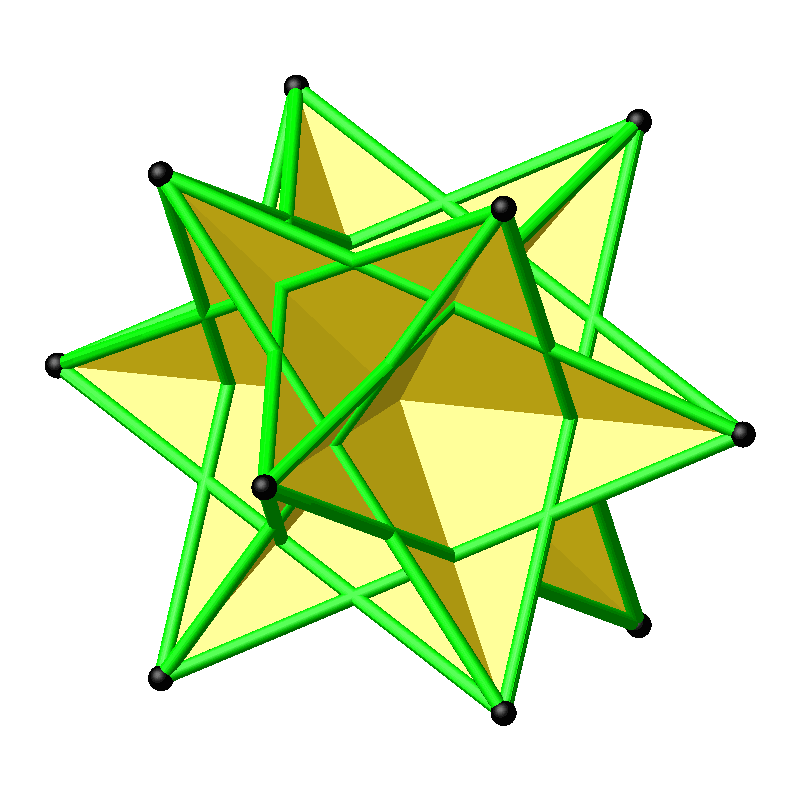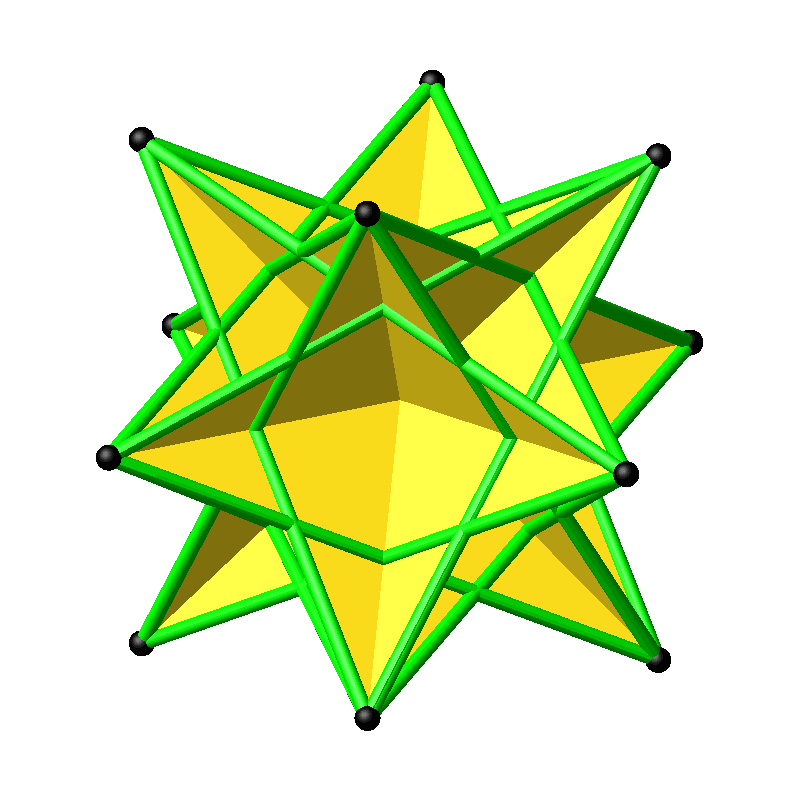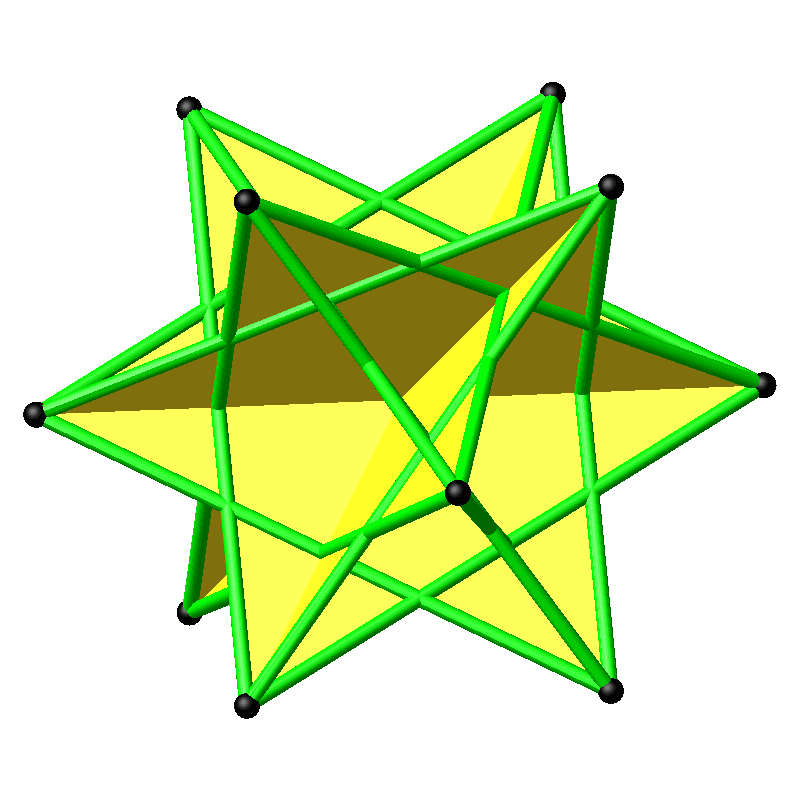
Abb. 12: Rotierende Davidsterne

4.2 Vierecke

Mit den Seitenquadraten des gewöhnlichen Kuboktaeders wird es noch spannender. Die Abbildung 13 zeigt ein solches Seitenquadrat.

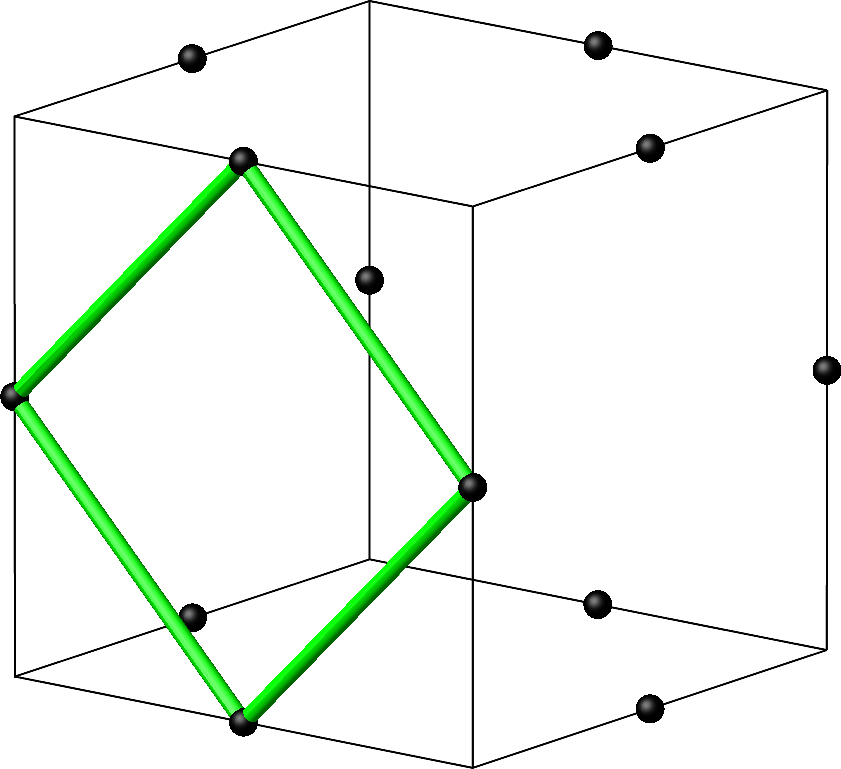
Abb. 13: Seitenquadrat des gewöhnlichen Kuboktaeders

Ich habe mich entschlossen, das entsprechende Viereck im großen Kuboktaeder gemäß Abbildung 14 zu sehen.

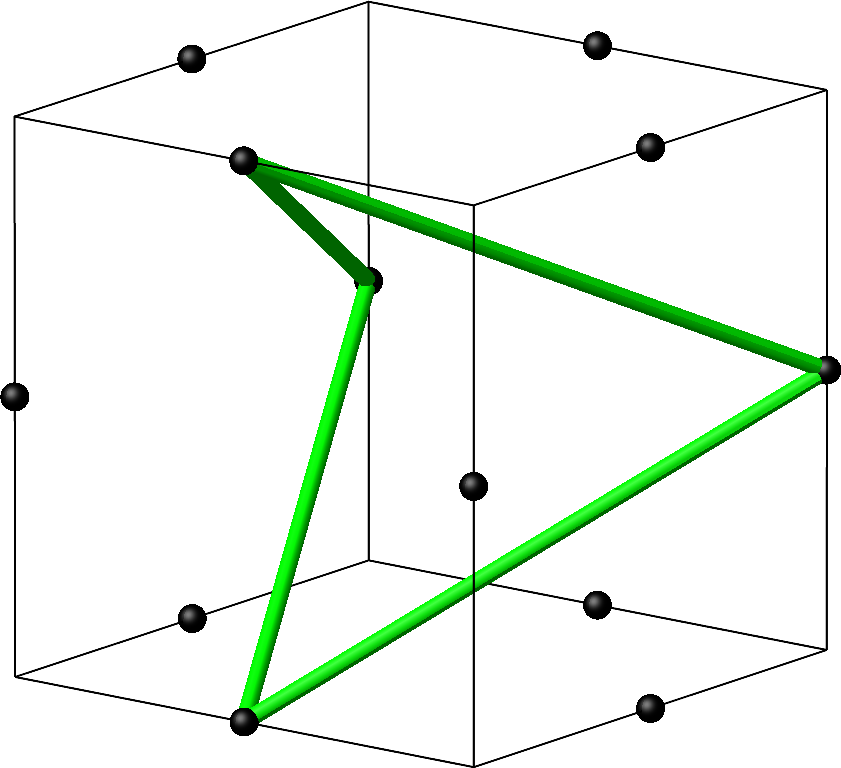
Abb. 14: Entsprechendes Viereck im großen Kuboktaeder

Das Viereck ist immer noch gleichseitig und gleichwinklig (wie das Quadrat), aber nicht mehr eben. Die Frage ist nun, wie man es hellblau ausmalt. Ich habe ein hellblaues hyperbolisches Paraboloid eingespannt (Abb. 15).

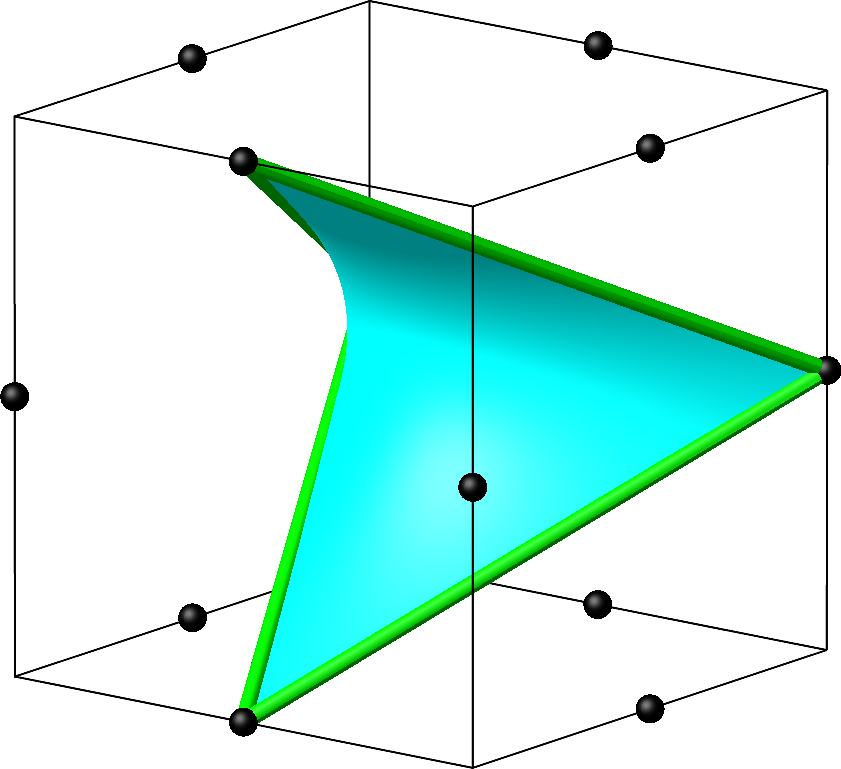
Abb. 15: Hyperbolisches Paraboloid

Es gibt insgesamt sechs solcher hyperbolischer Paraboloide (Abb. 16). Sie durchdringen sich gegenseitig.

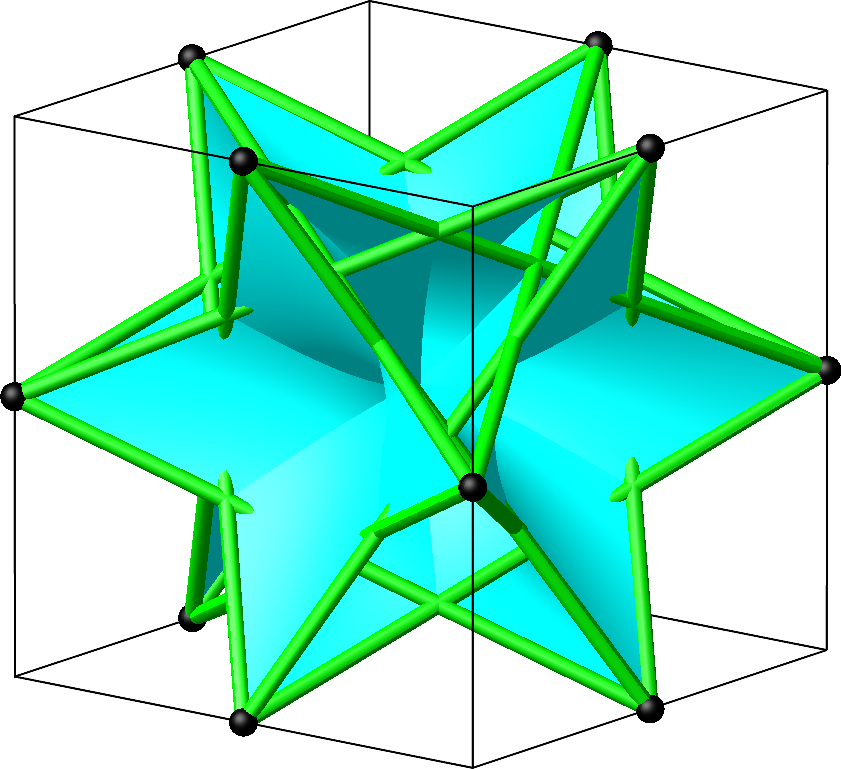
Abb. 16: Sechs hyperbolische Paraboloide

Beim Rotieren (Abb. 17) sehen wir durch das Modell hindurch. Dies wegen der fehlenden gelben Dreiecke.

Abb. 17: Rotation

4.3 Dreiecke und Vierecke

Die Abbildungen 18 und 19 zeigen das große Kuboktaeder.

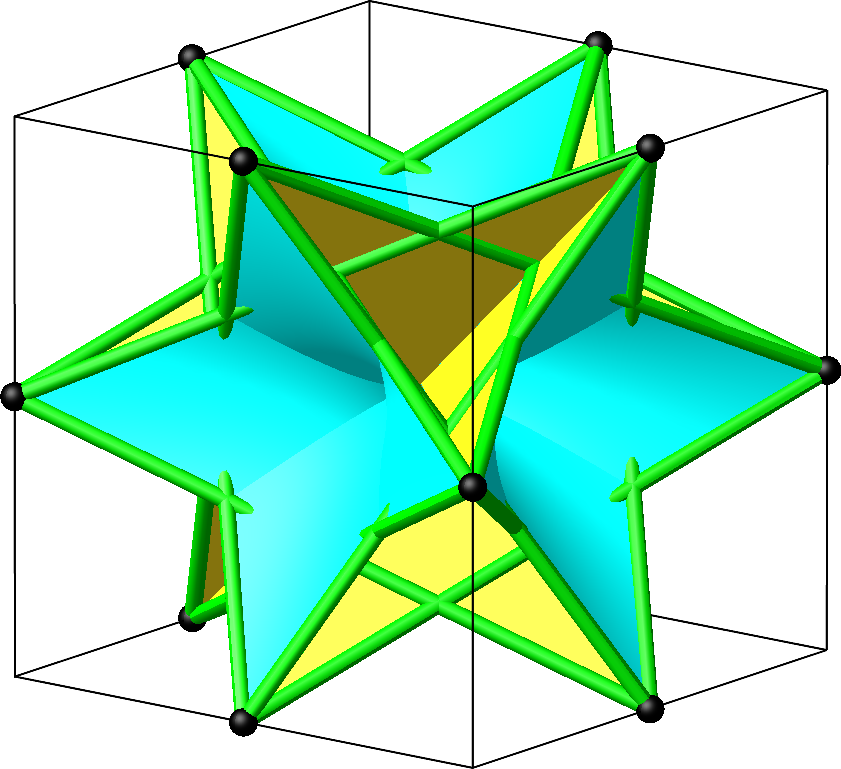
Abb. 18: Großes Kuboktaeder

Abb. 19: Rotierendes großes Kuboktaeder

Weblinks

Hans Walser: Kuboktaeder

https://www.walser-h-m.ch/hans/Miniaturen/K/Kuboktaeder/Kuboktaeder.htm

Hans Walser: Kuboktaeder-Kantenmodell

http://www.walser-h-m.ch/hans/Miniaturen/K/Kuboktaeder-Kantenmodell/Kuboktaeder-Kantenmodell.htm