1 Worum es geht

Sonderfall einer Schließungsfigur der Periodenlänge drei.

2 Die Schließungsfigur

Wir arbeiten mit der Hyperbel y = 1 – 1/x und der Geraden y = x (Abb. 1).

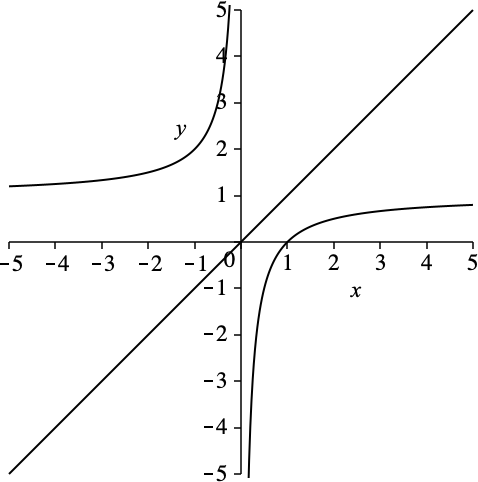
Abb. 1: Hyperbel und Gerade

Nun wählen wir auf der Hyperbel einen beliebigen Startpunkt (grün umrandet in Abb. 2). Von diesem Startpunkt aus fahren wir horizontal bis zur Geraden. Von dort vertikal bis zur Hyperbel. Dann wieder horizontal bis zur Geraden und vertikal zur Hyperbel. Dann nochmals horizontal bis zur Geraden und vertikal zur Hyperbel. Wir kommen zum Startpunkt zurück. Wir haben eine Schließungsfigur der Periodenlänge drei.

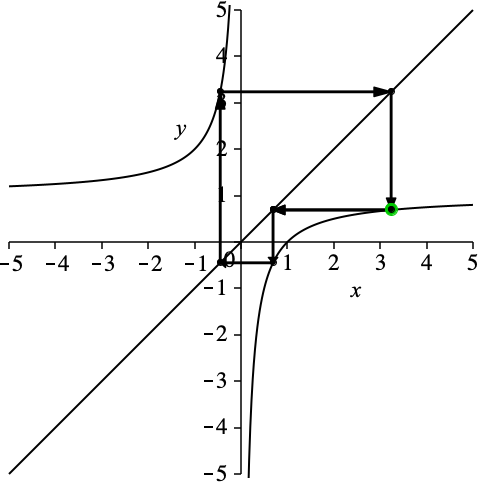
Abb. 2: Schließungsfigur

Die Schließungseigenschaft ist unabhängig von der Wahl des Startpunktes (Abb. 3).

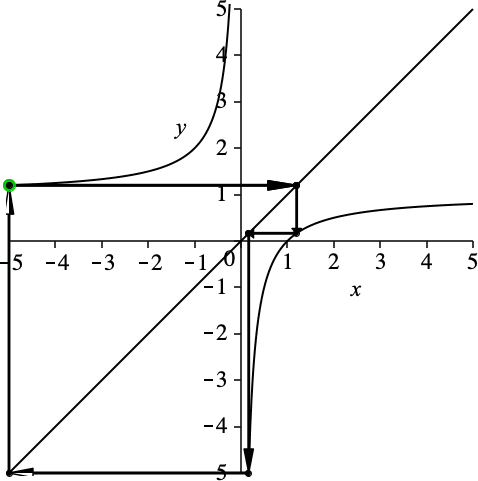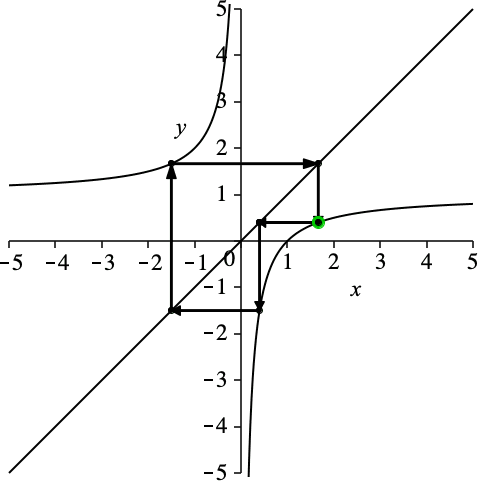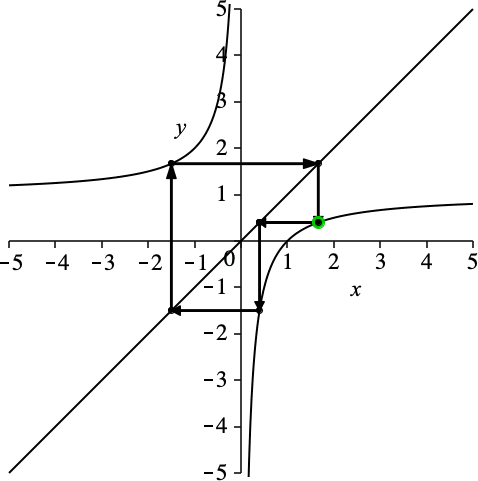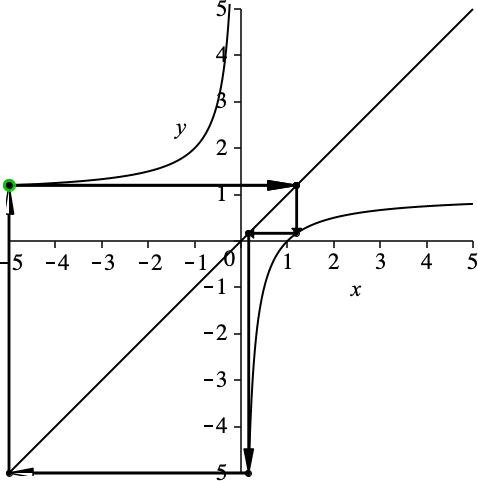
Abb. 3: Variation des Startpunktes

3 Spezielle Startpunkte

Wir schneiden die Hyperbel mit der Geraden y = –x (grün in Abb. 4). Die beiden Schnittpunkte haben Koordinaten im Kontext des Goldenen Schnittes.

Mit Φ = (1 + √5)/2 ≈ 1.618 (Goldener Schnitt) ergeben sich für die beiden Schnittpunkte die Koordinaten (–Φ, Φ) beziehungsweise (1/Φ, –1/Φ). Nachweis durch Rechnung.

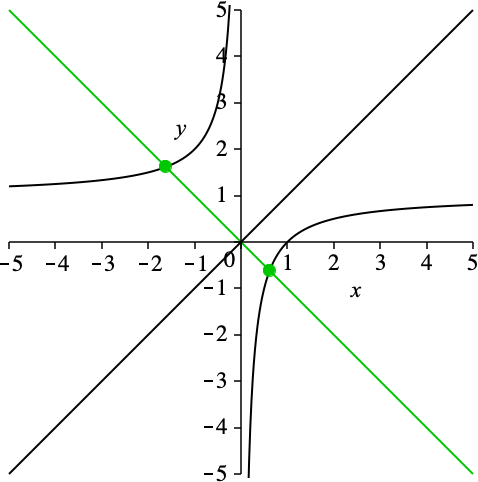
Abb. 4: Der Goldene Schnitt erscheint

Wir verwenden nun jeden dieser beiden Schnittpunkte als Startpunkt unserer Schließungsfigur (Abb. 5 und 6).

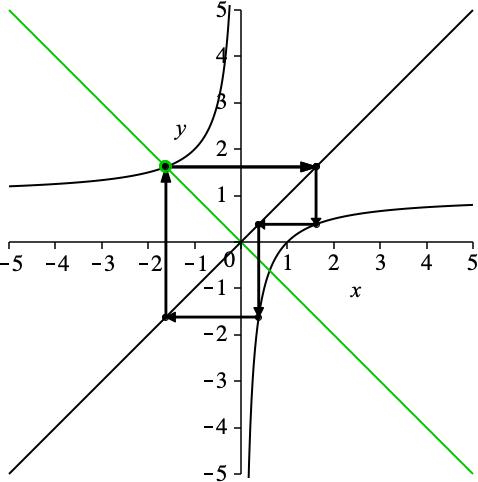
Abb. 5: Goldene Schließungsfigur

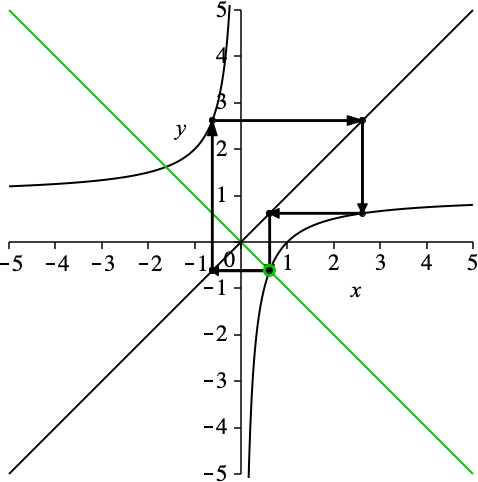
Abb. 6: Goldene Schließungsfigur

Die beiden Schließungsfiguren sind kongruent. Ihre Seitenlängen sind im Verhältnis Φ : 1 : (1/Φ).

4 Flächengleichheit

Das gelbe Quadrat und das hellblaue Rechteck sind flächengleich (Abb. 7).

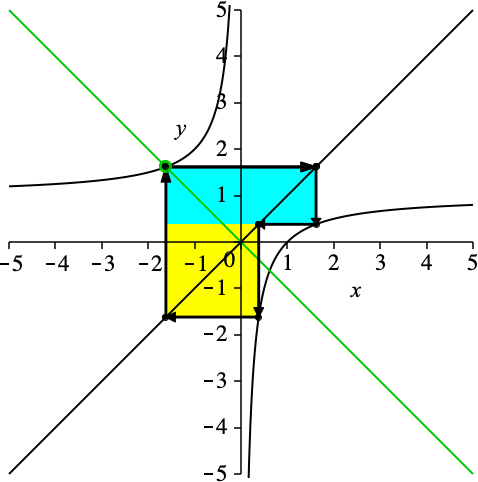
Abb. 7: Flächengleiche Vierecke

Weblinks

Hans Walser: Schließungsfigur

https://walser-h-m.ch/hans/Miniaturen/S/Schliessungsfigur4/Schliessungsfigur4.html

Hans Walser: Goldener Schnitt

https://walser-h-m.ch/hans/Miniaturen_Uebersicht/Goldener_Schnitt/index.html

Hans Walser: Schließungsfiguren

https://walser-h-m.ch/hans/Schliessungsfiguren/index.html