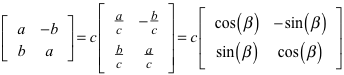Hans Walser, [20230502]

Ganzzahliges Dreieck

Anregung: Martin Lacher, PH Luzern

1 Problemstellung

Gesucht ist ein Dreieck, dessen Eckpunkte nur ganzzahlige Koordinaten haben, dessen Seitenlängen ganzzahlig sind und keine der Seiten parallel zur x- oder y-Achse liegt.

2 Pythagoreische Drehstreckung

Wir möchten ein Polygon mit ganzzahligen Eckpunktkoordinaten und ganzzahligen Seitenlängen mit einer Drehstreckung so abbilden, dass auch das Bildpolygon ganzzahlige Eckpunktkoordinaten und ganzzahligen Seitenlängen hat.

Dazu verwenden wir ein pythagoreisches Dreieck mit den Kathetenlängen a und b und der Hypotenusenlänge c. Es sind also a, b und c ganzzahlig.

Die Matrix

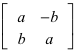
beschreibt eine Drehstreckung um den Ursprung um den Winkel β des pythagoreischen Dreiecks und dem Streckfaktor c.

Begründung: Wir können die Matrix umschreiben:

Der Faktor c beschreibt die Streckung, die verbleibende Matrix die Drehung um den Winkel β.

Entsprechend beschreibt die Matrix

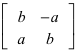
eine Drehstreckung um den Winkel α.

Die Abbildungsgleichungen sind linear und haben ganzzahligen Koeffizienten. Daher werden ganzzahlige Koordinaten auf ganzzahlige Koordinaten abgebildet. Der Streckfaktor ist ganzzahlig, daher werden ganzzahlige Längen auf ganzzahlige Längen abgebildet.

Beispiel:

Das „Lehrerdreieck“ mit den Seitenlänge 3, 4, 5 ergibt die Drehstreckung:

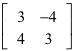
Bei dieser Drehstreckung wird um den Ursprung um den Winkel β = arctan(4/3) ≈ 53.13° gedreht und mit dem Faktor 5 gestreckt.

Die Abbildung 1 zeigt die Situation mit dem Einheitsquadrat als Startfigur.

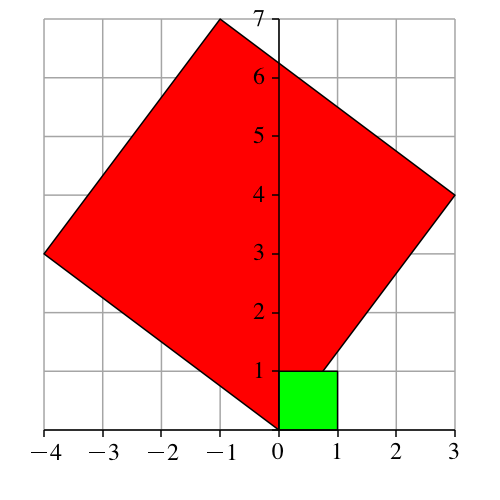
Abb. 1: Drehstreckung

3 Bearbeitung der Problemstellung

Der Trick besteht nun darin, zuerst ein Dreieck aus pythagoreischen Dreiecken zusammenzustellen. Dabei ergibt sich in der Regel eine Figur mit mindestens einer zu den Koordinatenachsen parallelen Seiten. Mit einer pythagoreischen Drehstreckung kann dies ausgehebelt werden.

3.1 Rechtwinkliges Dreieck

Es genügt, ein pythagoreisches Dreieck in der üblichen Darstellung A(b, c), B(0,0), C(b, 0) einer pythagoreischen Drehstreckung zu unterwerfen (Abb. 2).

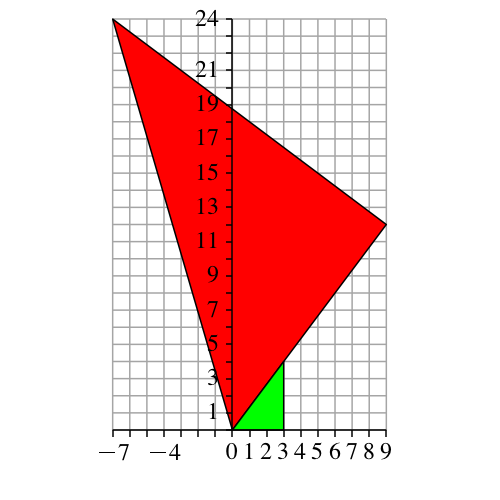
Abb. 2: Rechtwinkliges Dreieck

3.2 Gleichschenkliges Dreieck

Wir setzen aus zwei kongruenten pythagoreischen Dreiecken ein gleichschenkliges Dreieck zusammen und führen eine pythagoreische Drehstreckung durch (Abb. 3).

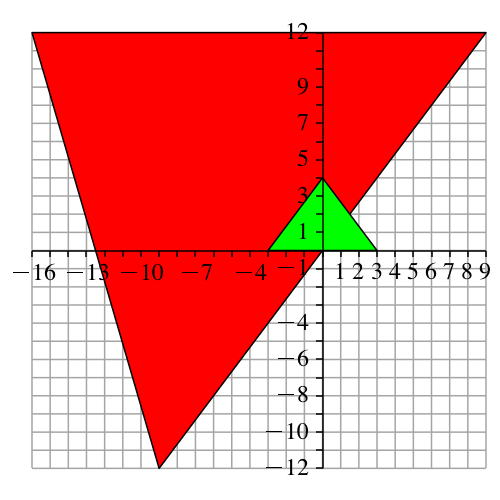
Abb. 3: Au weia!

Jetzt sind wir auf die Nase gefallen. Ein Schenkel des roten Dreiecks ist parallel zur x-Achse.

Aber wir haben ja noch eine zweite Drehstreckung zur Verfügung (Abb. 4).

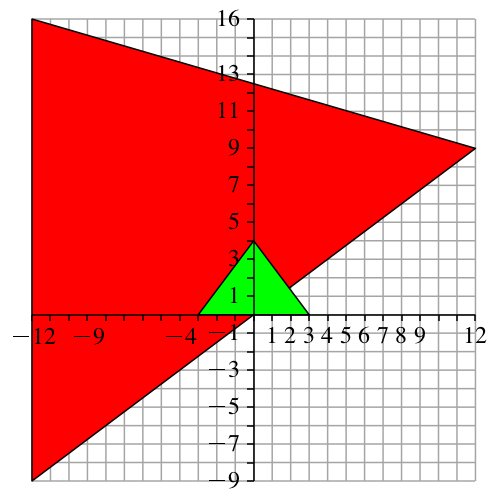
Abb. 4: Geht auch nicht

Leider geht auch dies nicht.

Nun gibt es aber unendlich viele pythagoreische Dreiecke. Statt ausschließlich mit dem Lehrerdreieck zu arbeiten, können wir zum Beispiel auch das pythagoreische Dreieck mit den Seitenlängen 5, 12, 13 ins Spiel bringen (Abb.5).

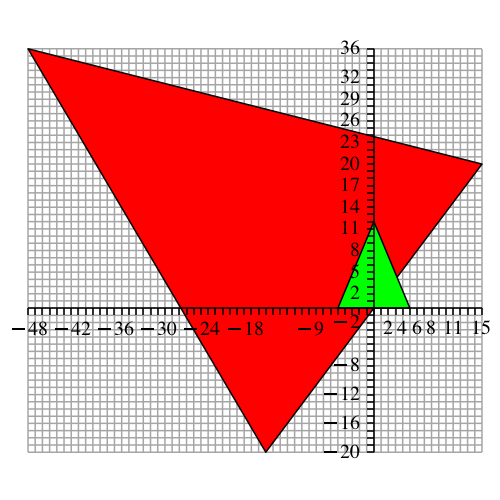
Abb. 5: Gleichschenkliges Dreieck

3.3 Allgemeines Dreieck

Wir beginnen mit zwei verschiedenen pythagoreischen Dreiecken und vergrößern sie so, dass zwei Kathetenlängen (je eine von jedem der beiden Dreiecke) übereinstimmen. Diese übereinstimmende Länge ist ein gemeinsames Vielfaches der ursprünglichen Längen. Sinnvollerweise arbeitet man mit dem kgV (kleinstes gemeinsames Vielfache).

Im Beispiel der Abbildung 6 ist im grünen Startdreieck links das Lehrerdreieck mit dem Faktor 3 vergrößert worden, damit wir rechts das Dreieck mit den Seiten 12, 5 13 ansetzen können. Für die Drehstreckung wurde wiederum das Lehrerdreieck verwendet.

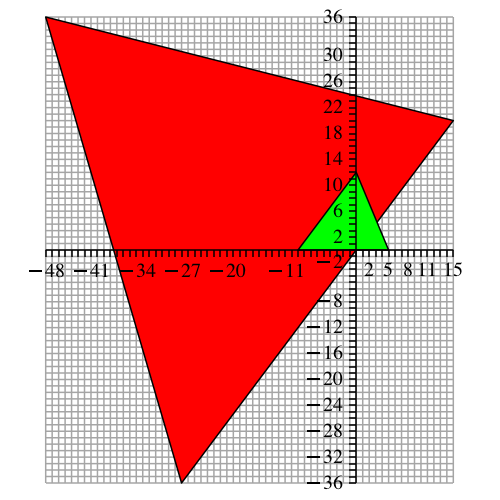
Abb. 6: Allgemeines Dreieck

Im roten Dreieck haben wir die Eckpunktkoordinaten A(–27, –36), B(15, 20), C(–48, 36) und die Seitenlängen a = 65, b = 75, c = 70.

4 Im Raum

Die Matrix

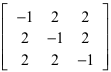
beschreibt eine Drehstreckung im Raum. Drehachse ist die Gerade durch den Ursprung und den Punkt (1, 1, 1), der Drehwinkel ist 180° und der Streckfaktor 3.

Die Abbildungsgleichungen sind linear und haben ganzzahligen Koeffizienten. Daher werden ganzzahlige Koordinaten auf ganzzahlige Koordinaten abgebildet. Der Streckfaktor ist ganzzahlig, daher werden ganzzahlige Längen auf ganzzahlige Längen abgebildet.

Im Beispiel der Abbildung 7 gehen wir aus vom grünen Lehrerdreieck mit den Eckpunktkoordinaten (3, 4, 0), (0, 0, 0), (3,0, 0). Das Dreieck liegt also in der x,y-Ebene.

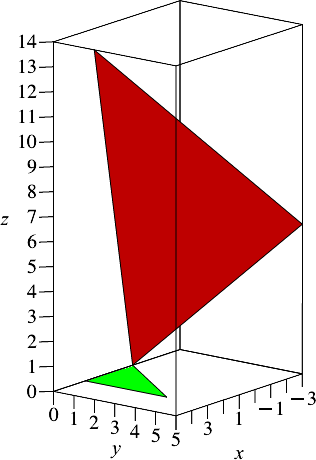
Abb. 7: Beispiel im Raum

Durch die Drehstreckung ergibt sich das rote Dreieck mit den Eckpunktkoordinaten A(5, 2, 14), B(0, 0, 0), C(–3, 6, 6). Es hat die Seitenlängen a = 9, b = 12, c = 15.