Hans Walser, [20060507a], [20131229b]

The golden section and lattice geometry

1 Working on a chessboard

Let n be an integer number such that both n and are sums of two square numbers. In this case the proportion of the golden section can be constructed in a square lattice, using circles going through lattice points.

It’s a kind of geometry on a chessboard.

Chessboard

1.1 Example

In the case of we have:

This gives the solution:

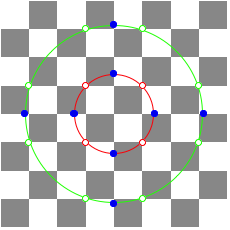
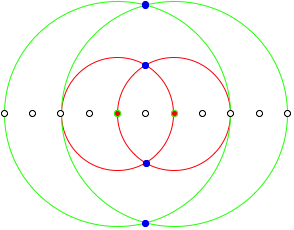
Where is the golden section?

In the labeling of the following figure the point B divides the segment AC in the proportion of the golden section.

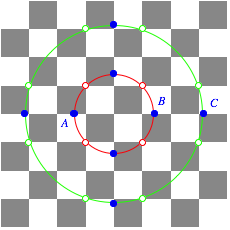
The point B divides the segment AC in the golden proportion

The red circle has its midpoint in the origin and passes through , its radius is . The green circle is also around the origin and passes through . Its radius is . Therefore we have:

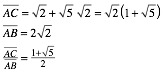
The number indicates the golden section ([Walser 2001], p. 4).

1.2 General case

This works also in general. From

we get the red circle around the origin and passing trough with radius and the green circle with the same midpoint, going through and radius . Working with the corresponding points as in the particular case above we have:

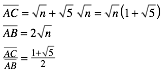
1.3 Further examples

1.3.1 n = 1

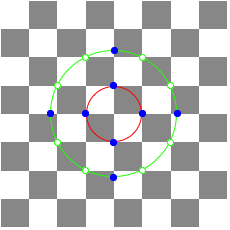
n = 1

In this case the blue points on the red circle are lattice points.

1.3.2 n = 2

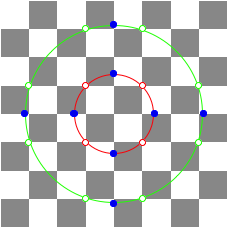
n = 2

1.3.3 n = 5

Here we have to enlarge the chessboard.

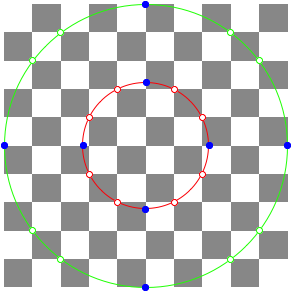
n = 5

Of course we could also work with the decomposition:

1.3.4 n = 10

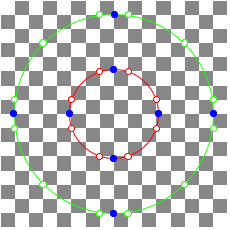
n = 10

1.3.5 n = 13

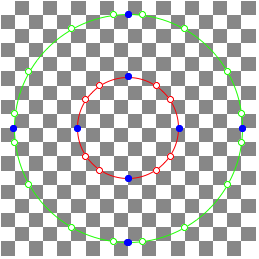
n = 13

2 Working on an integer baseline

Let n be an integer number such that both n and are differences of two square numbers. In this case the proportion of the golden section can be constructed in an integer baseline, using circles with integer radii.

2.1 Example

Where is the golden section?

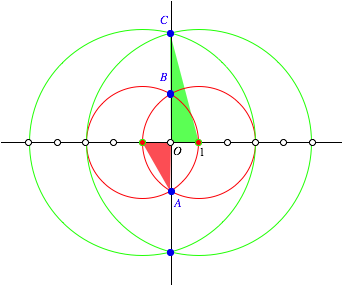
How to see it

In the red triangle we have and in the green triangle . Therefore:

This works also in general. The proof is left to the reader.

We see that in our Example only every second mark of the baseline is used. Therefore we can simplify the figure in omitting every second mark. And using a nice coloring we get the following result.

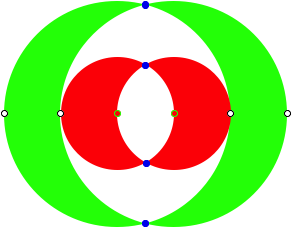
Crescents

2.2 Further examples

2.2.1 n = 3

We had already this solution:

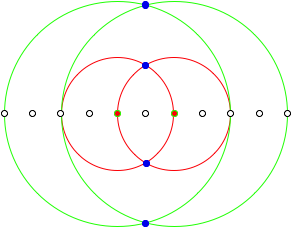
n = 3

But there is a second solution:

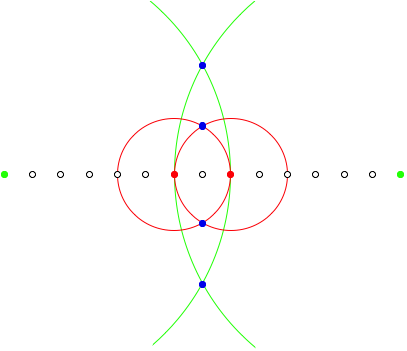
Second solution

In this case the proof uses the following triangles:

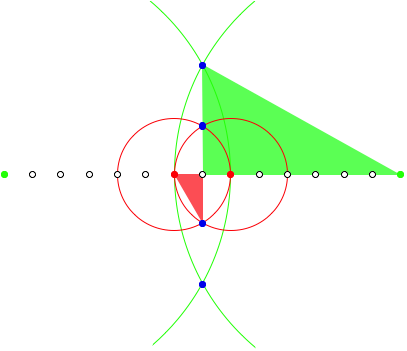
Proof Figure

2.2.2 n = 4

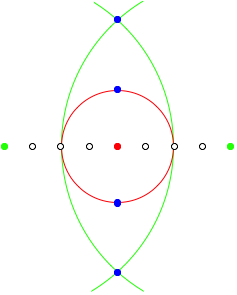
n = 4

2.2.3 n = 7

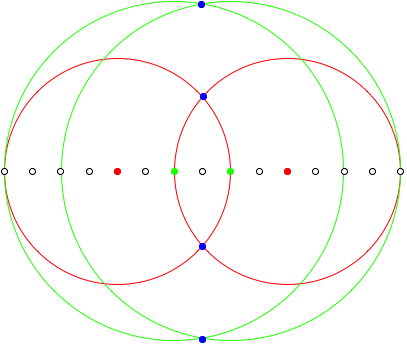
n = 7

2.2.4 n = 8

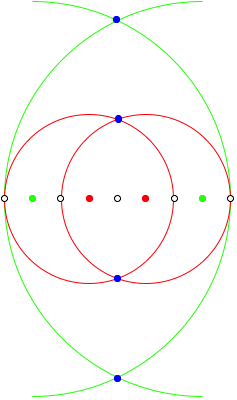
n = 8

2.2.5 n = 9

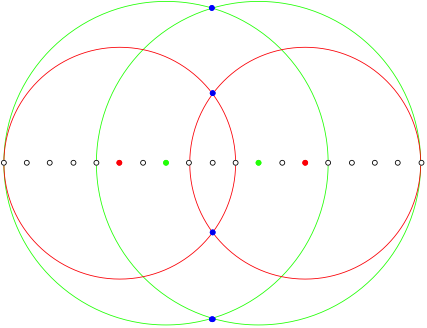
n = 9

There is of course an other solution.

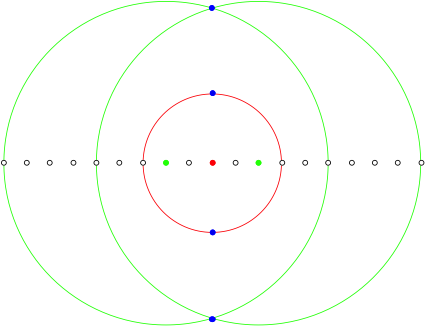
n = 9, other solution

2.2.6 n = 11

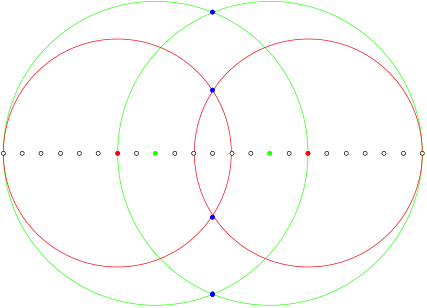
n = 11

2.2.7 n = 12

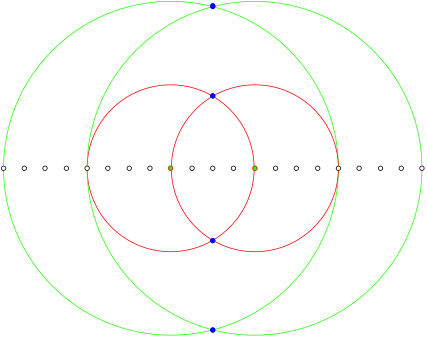
n = 12

This figure we had already in the case n = 3, but here zoomed by the factor 2. This is obvious, since

And so on. The reader will easily find other examples.

3 Chessboard an circles

3.1 Example

In the case of

we have n as difference and 5n as sum of two squares. Therefore we have to combine the two methods from above.

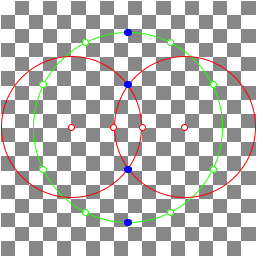
n = 9

3.2 An other example

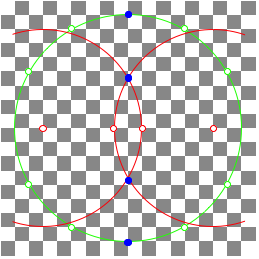
n = 13

Acknowledgment

The author would like to thank Jo Niemeyer (Schluchsee, Germany) for helpful suggestions.

Reference

[Walser 2001] Walser, Hans: The Golden Section. Translated by Peter Hilton and Jean Pedersen. The Mathematical Association of America 2001. ISBN 0-88385-534-8