Hans Walser, [20090715c]

Fibonacci in the Triangular Lattice

1 The Fibonacci Triangle

In a regular triangular lattice we draw on top a red regular unit triangle, underneath a yellow rhombus and beneath a second red triangle. Under the red triangle an other yellow rhombus and beneath a red isosceles trapezium. And now always under the red trapezium a yellow rhombus and under the yellow rhombus a red trapezium.

Filling the triangle with trapeziums and rhombuses

Now the sides of the rhombuses are the Fibonacci numbers. The top side of a trapezium, the two isosceles sides and the base are three consecutive Fibonacci numbers.

The proof is simple:

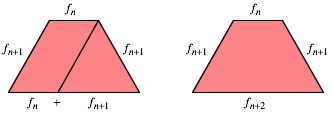
Proof

2 The Fibonacci Hexagon

Just for fun: The Fibonacci Hexagon.

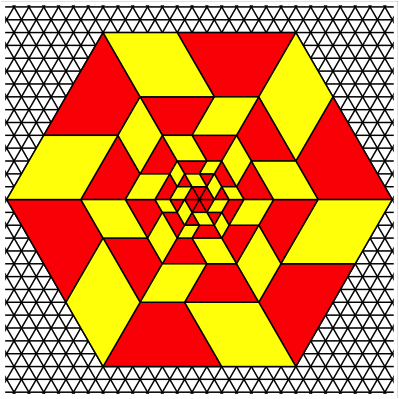
Fibonacci Hexagon

3 Stars

We can remove the rhombuses and reassemble the trapezoids to get a star.

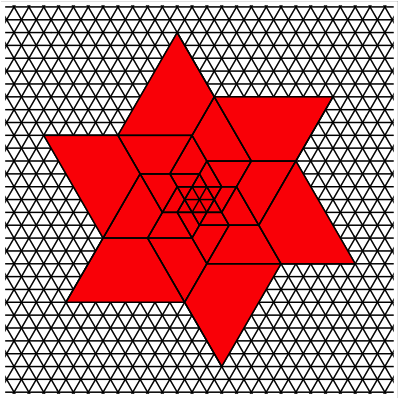
Fibonacci Star

And of course we can also reassemble the rhombuses to get another star.

Another Fibonacci Star

4 Proof without words

The Fibonacci Triangle again

Using the Fibonacci Triangle we can prove the identity:

5 Variations in the Square Lattice

We can transfer the Fibonacci triangle into a square lattice. Compare with the Matterhorn in the Swiss Alps.

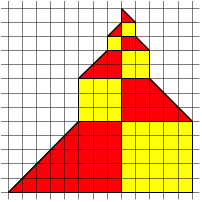
In the Square Lattice. Matterhorn

Just Lines