Hans Walser, [20090331a]

Teilfolgen der Fibonacci-Folge

1 Worum geht es?

Wir wählen aus der Fibonacci-Folge

1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	1	2	3	5	8	13	21	34	55	89	144	233	377

Teilfolgen aus und fragen nach deren Rekursionsformel.

Die Ideen gehen auf Édouard Lucas zurück.

2 Beispiele

2.1 Die Fibonacci-Folge

Die Fibonacci-Folge selber hat die Rekursion:

Es gilt die explizite Formel von Binet:

Die Fibonacci-Folge ist auch für negative Indizes definiert:

-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
-8	5	-3	2	-1	1	0	1	1	2	3	5	8

2.2 Teilfolgen mit nur jeder zweiten Fibonacci Zahl

Wir wählen aus der Fibonacci-Folge nur jede zweite Zahl aus, erhalten somit die beiden Folgen:

1	2	3	4	5	6	7	8	9	10	11	12
1	2	5	13	34	89	233	610	1597	4181	10946	28657
1	3	8	21	55	144	377	987	2584	6765	17711	46368

Beide Folgen haben dieselbe Rekursion, nämlich:

2.3 Teilfolgen mit nur jeder dritten Fibonacci Zahl

Wir wählen aus der Fibonacci-Folge nur jede dritte Zahl aus, erhalten somit die drei Folgen:

1	2	3	4	5	6	7	8	9	10	11
1	3	13	55	233	987	4181	17711	75025	317811	1346269
1	5	21	89	377	1597	6765	28657	121393	514229	2178309
2	8	34	144	610	2584	10946	46368	196418	832040	3524578

Diese drei Folgen haben dieselbe Rekursion, nämlich:

2.4 Teilfolgen mit nur jeder vierten Fibonacci Zahl

Wir wählen aus der Fibonacci-Folge nur jede vierte Zahl aus, erhalten somit die vier Folgen:

1	2	3	4	5	6	7	8	9	10
1	5	34	233	1597	10946	75025	514229	3524578	24157817
1	8	55	377	2584	17711	121393	832040	5702887	39088169
2	13	89	610	4181	28657	196418	1346269	9227465	63245986
3	21	144	987	6765	46368	317811	2178309	14930352	102334155

Die vier Folgen haben dieselbe Rekursion, nämlich:

2.5 Zusammenstellung

Wir haben der Reihe nach die Rekursionsformeln:

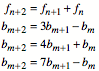
Wir vermuten, dass die Formeln im ersten Koeffizienten die Zahlen der Folge

1	2	3	4	5	6	7	8	9	10	11	12	13	14
1	3	4	7	11	18	29	47	76	123	199	322	521	843

haben und im zweiten Summanden ein alternierendes Vorzeichen. Diese Zahlen sind die Lucas-Zahlen, benannt nach Édouard Lucas (1842–1891). Die Lucas-Zahlen haben dieselbe Rekursion wie die Fibonacci-Zahlen.

Wir prüfen die Vermutung am Beispiel, in welchem wir nur jede fünfte Zahl der Fibonacci-Zahlen nehmen. Diese Teilfolgen müssten der Rekursion genügen. Das sieht so aus:

1	2	3	4	5	6	7	8	9
1	8	89	987	10946	121393	1346269	14930352	165580141
1	13	144	1597	17711	196418	2178309	24157817	267914296
2	21	233	2584	28657	317811	3524578	39088169	433494437
3	34	377	4181	46368	514229	5702887	63245986	701408733
5	55	610	6765	75025	832040	9227465	102334155	1134903170

Die Vermutung ist bestätigt.

Wie lassen sich diese Vermutungen beweisen?

3 Beweis

Der Beweis läuft in drei Schritten.

3.1 Die Formel von Binet für die Lucas-Zahlen

Die Lucas-Zahlen lassen sich mit folgender Formel explizit erzeugen:

Beweis induktiv:

(I)

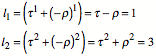
(II)

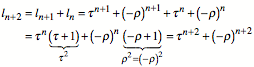
3.2 Quotientenfolge

3.2.1 Fibonacci-Zahlen

Die Quotienten aufeinander folgender Fibonacci-Zahlen streben gegen den goldenen Schnitt:

Wir können die Fibonacci-Zahlen auch rückwärts laufen lassen und erhalten:

Diese beiden Grenzwerte sind die Lösungen der quadratischen Gleichung:

3.3 Fibonacci-Teilfolgen

Wir wählen aus der Fibonacci-Folge Zahlen im Abstand k aus. Die Quotientenfolge dieser Teilfolge hat die Limites und . Dies sind die Lösungen der quadratischen Gleichung:

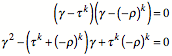
Vergleich mit liefert:

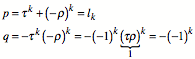
Die Teilfolge hat also die Rekursion:

Damit ist die Vermutung bewiesen.

Die Überlegungen sind unabhängig von den Startwerten der Fibonacci-Folge und gelten daher für jede Folge mit derselben Rekursion.

4 Variante

Wir arbeiten mit der abgeänderten Rekursion:

4.1 Die Folge

Aus ergibt sich mit den Stützwerten und die Folge:

-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
99	-41	17	-7	3	-1	1	1	3	7	17	41	99

Die Folge, die übrigens nur aus ungeraden Zahlen besteht, hat die explizite Formel:

Weiter ist:

4.2 Teilfolgen

Wir wählen jedes zweite Glied der Folge aus:

-5	-4	-3	-2	-1	0	1	2	3	4	5
-8119	-1393	-239	-41	-7	-1	1	7	41	239	1393
3363	577	99	17	3	1	3	17	99	577	3363

Beide Folgen haben dieselbe Rekursion, nämlich:

Wir wählen jedes dritte Glied der Folge aus:

-4	-3	-2	-1	0	1	2	3	4
114243	-8119	577	-41	3	1	17	239	3363
-47321	3363	-239	17	-1	3	41	577	8119
19601	-1393	99	-7	1	7	99	1393	19601

Diese drei Folgen haben dieselbe Rekursion, nämlich:

Wir wählen jedes vierte Glied der Folge aus:

-4	-3	-2	-1	0	1	2	3	4
-9369319	-275807	-8119	-239	-7	1	41	1393	47321
3880899	114243	3363	99	3	3	99	3363	114243
-1607521	-47321	-1393	-41	-1	7	239	8119	275807
665857	19601	577	17	1	17	577	19601	665857

Diese vier Folgen haben dieselbe Rekursion, nämlich:

4.3 Zusammenstellung und Übersicht

Wir haben der Reihe nach die Rekursionen:

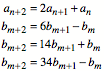
Beim Summanden mit haben wir alternierende Vorzeichen, beim Summanden mit bilden die Koeffizienten die Folge

-6	-5	-4	-3	-2	-1	0	1	2	3	4	5	6
198	-82	34	-14	6	-2	2	2	6	14	34	82	198

Diese den Lucas-Zahlen entsprechende Folge hat ebenfalls die Rekursion:

Ihre explizite Formel ist:

Sie ist das Doppelte der Folge .

Analog zur Fibonacci-Folge kann gezeigt werden, dass für eine Auswahl mit Abstand k aus unserer Folge die Rekursion

hat.

5 Verallgemeinerung

Die beiden Beispiele passen ins folgende allgemeine Schema.

5.1 Die Folge

Wir studieren eine Folge mit beliebigen Startwerten und der Rekursion:

5.2 Quotientenfolge

Wir bilden die Quotientenfolge und erhalten:

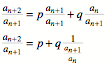
Für die Grenzwerte gilt somit:

Nun seien die Lösungen dieser Gleichung, also:

Damit gilt:

Ferner ist (Satz von Vieta):

5.3 Explizite Formel

Die Folge kann explizit angegeben werden durch:

Die Koeffizienten und ergeben sich durch Einsetzen der Startwerte.

5.4 Analogon zu den Lucas-Zahlen

Die Folge

ist das Analogon zu den Lucas-Zahlen. Diese Folge ist ein Sonderfall von und hat dieselbe Rekursion . Im Einzelnen ist:

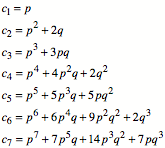
5.5 Auswahl

Wir wählen nun aus der Folge jedes k-te Element aus und bilden damit die Folge , also:

Es gibt also k verschiedene Folgen , je nach Ausgangsindex j.

Dann gilt für die Folgen die Rekursion:

5.6 Beweis

Es ist zu verifizieren:

Also:

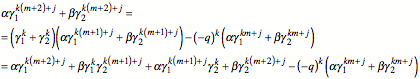
Somit bleibt noch zu verifizieren:

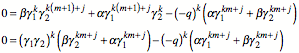
Wegen stimmt das.