Hans Walser, [20150815]

Fibonacci-erzeugende Funktion

Anregung: (Hong, 2015)

1     Worum geht es?

Wir arbeiten mit der verallgemeinerten Fibonacci-Folge  mit den Startwerten  und  und der Rekursion:

 

                                                                                                         (1)

 

Wir suchen nun eine erzeugende Funktion, also eine (formale) Potenzreihe von der Form:

 

                                                                           (2)

 

2     Folgenglieder

Die Tabelle 1 zeigt die ersten Folgenglieder.

n

0

1

2

3

4

5

Tab. 1: Folgenglieder

Fźr  und die Startwerte  ergibt sich die gewšhnliche Fibonacci-Folge.

3     Erzeugende Funktion

Die Funktion

 

                                                                                                        (3)

 

leistet das Gewźnschte, wie durch Rźckrechnen eingesehen werden kann. Zu zeigen ist:

 

                                      (4)

 

Fźr das Produkt auf der rechten Seite von (4) erhalten wir:

 

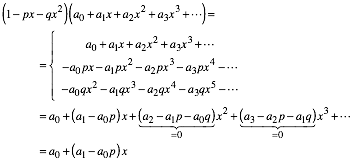                    (5)

 

 

 

 

 

 

 

 

Wegen der Rekursion (1) verschwinden die Koeffizienten fźr  und hšhere Potenzen von x. Damit sind (4) und (3) bewiesen.

3.1    Beispiele

3.1.1   Fibonacci

Fźr  und die Startwerte  ergibt sich:

 

                             (6)

 

Die Abbildung 1 zeigt den Grafen dieser Funktion.

 

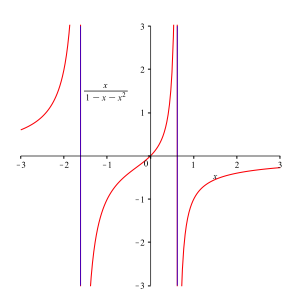
Abb. 1: Funktionsgraf

 

3.1.2   p = 2

Fźr  und die Startwerte  ergibt sich:

 

               (7)

 

Die Abbildung 2 zeigt den Grafen dieser Funktion.

 

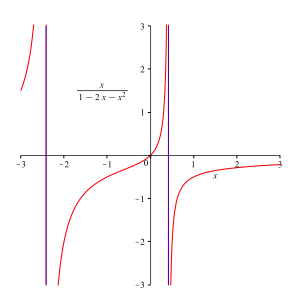
Abb. 2: Funktionsgraf

 

4     Quotientenfolge

Wir bilden nun die Quotientenfolge:

 

                                                                                                                         (8)

 

Nebenbemerkung: Es ist (nicht mit der schulischen p-q-Formel verwechseln):

 

                                                 (10)

 

Man kann sich źberlegen, was die zweite Formel von (10) bedeutet.

Weiter sei nun:

 

                                                                                                                     (11)

 

4.1    Beispiele

4.1.1   Fibonacci

Fźr  und die Startwerte  ergeben sich die Werte der Tabelle 2.

 

n

0

0

0

0

1

1

1

–1

2

1

2

3

2

–6

4

3

15

5

5

–40

Tab. 2: Fibonacci

 

4.1.2   p = 2

Fźr  und die Startwerte  ergeben sich die Werte der Tabelle 3.

 

n

0

0

0

0

1

1

–2

2

2

10

3

5

–60

4

12

348

5

29

–2030

Tab. 3

 

4.1.3   q = 2

Fźr  und die Startwerte  ergeben sich die Werte der Tabelle 4. Die Werte der Folge  sind nicht mehr ganzzahlig. Der Einfluss von q = 2 ist offensichtlich.

 

n

0

0

0

0

1

1

1

2

1

3

3

4

5

5

11

Tab. 4

 

5     Tribonacci

Die Folge  genźgt folgender Rekursion:

 

                                                                             (12)

 

Wir haben eine so genannte Tribonacci-Folge.

Beweis fehlt, experimentell erhŠrtet.

Die Startwerte  und  der ursprźnglichen Folge haben keinen Einfluss auf die Rekursion (12). Hingegen hŠngen die Startwerte der Folge  von den Starwerten der ursprźnglichen Folge ab:

 

                                 (13)

 

Fźr q = 1 und ganzzahlige Startwerte sowie ganzzahliges p sind die Werte von  ganzzahlig.

Die Folge  hat mit der Schreibweise

 

                                                                                       (14)

 

die erzeugende Funktion:

 

                                                                                 (15)

 

Literatur

Hong, Dae S. (2015): When is the Generating Function of the Fibonacci Numbers an Integer? The College Mathematics Journal. Vol. 46, No. 2, March 2015, 110-112.