Hans Walser, [20180810]
Falsche Schraubenlinie
Anregung: Wunder (2018)
1 Worum geht es?
Der Handlauf eines TreppengelŠnders konstanter Steigung, das aber ãum die Ecke gehtÒ, kann an der Ecke durch einen Bogen abgerundet werden. Was kann Ÿber die Steigung auf diesem BogenstŸck gesagt werden?
Es zeigt sich, dass die Steigung auf dem BogenstŸck grš§er ist als die konstante Steigung auf den geraden StŸcken.
Es wird exemplarisch mit dem einfachsten Fall ausgehen von der Steigung 1, gearbeitet. Dabei treffen wir auf das DIN-Format und den kristallografischen Winkel.
2 Echte Schraubenlinie
Die Abbildung 1a zeigt eine echte Schraubenlinie mit der Steigung 1 (also dem Steigungswinkel 45¡). Die Schraubenlinie liegt auf einem Kreiszylinder.
Die Abbildung 1b zeigt die zugehšrige Abwicklung.
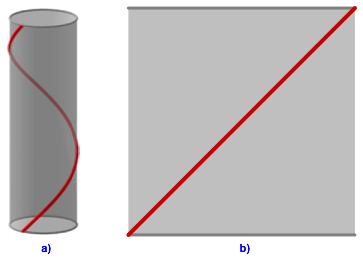
Abb. 1: Schraubenlinie und Abwicklung
3 Eckige Schraubenlinie
Die Abbildung 2 zeigt einen WŸrfel mit einer Ÿbereck laufenden roten Linie.
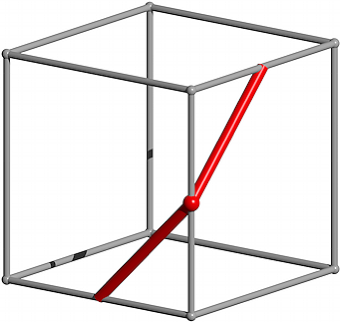
Abb. 2: WŸrfel mit roter Linie
Wenn wir vier solche Figuren der Abbildung 2 je um 90¡ verdreht aufeinandersetzen, erhalten wir eine eckige Schraubenlinie (Abb. 3a).
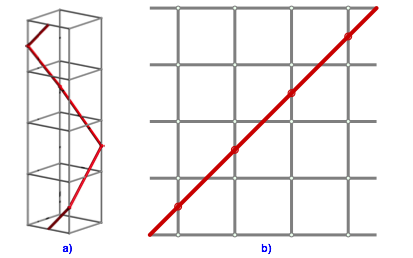
Abb. 3: Eckige Schraubenlinie. Abwicklung
Die Abbildung 3b zeigt die Abwicklung dieser eckigen Spirale. Sie ist wesentlich dieselbe Figur wie die Abwicklung der Schraubenlinie (Abb. 1b). Die Steigung ist ebenfalls konstant 1, der Steigungswinkel 45¡.
4 Abrundung durch einen Bogen
Die beiden roten Teilstrecken der Abbildung 2 schlie§en einen Winkel ein, allerdings keinen rechten Winkel. Um diesen Winkel zu bestimmen, ergŠnzen wir die Figur mit vier weiteren analogen Teilstrecken zu einem regelmŠ§igen Sechseck (Abb. 4).
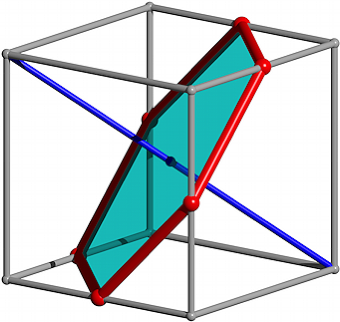
Abb. 4: RegelmŠ§iges Sechseck
Das Sechseck ist die Schnittfigur des WŸrfels mit der Mittelnormalebene der eingezeichneten WŸrfeldiagonale.
Die Au§enwinkel des regelmŠ§igen Sechsecks sind 60¡. Dies ist die RichtungsŠnderung zweier aufeinanderfolgender roten Strecken.
Wir kšnnen also die durch die beiden roten Teilstrecken der Abbildung 2 gebildete Ecke durch einen 60¡-Bogen abrunden. Der Radius dieses Bogens ist frei. Wir wŠhlen ihn gemŠ§ Abbildung 5.
In der Abbildung 5 sind zusŠtzlich das Zentrum und die Grenzradien des Bogens eingezeichnet. Der Bogen ist nicht Teil des Inkreises des regelmŠ§igen Sechseckes der Abbildung 4.
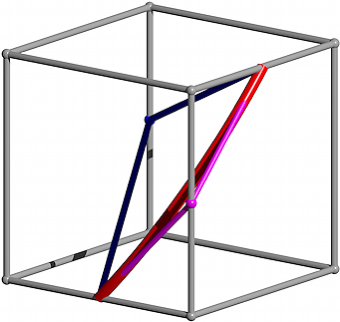
Abb. 5: Bogen
5 Falsche Schraubenlinie
5.1 Ansicht
Wenn wir vier solche Figuren der Abbildung 5 je um 90¡ verdreht aufeinandersetzen, erhalten wir eine falsche Schraubenlinie (Abb. 6b). Sie ist aus vier 60¡-Bšgen zusammengesetzt.
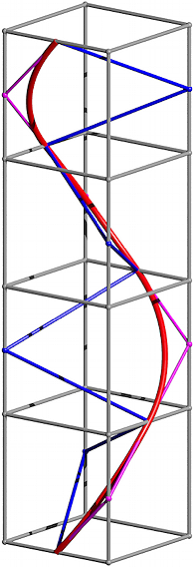
a) b)
Abb. 6: Falsche Schraubenlinie
5.2 Steigung
In der Abbildung 6a ist in magenta die eckige Schraubenlinie der Abbildung 3 sichtbar. Die falsche Schraubenlinie ist kŸrzer (sie lŠuft der eckigen Schraubenlinie den Rank ab), schafft aber dieselbe Hšhendifferenz. Sie hat daher im Mittel eine grš§ere Steigung als die eckige Schraubenlinie.
5.3 Sicht von oben
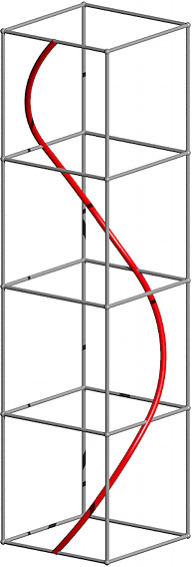
Die Abbildung 7 zeigt die Sicht von oben.
Abb. 7: Sicht von oben
Die
falsche Schraubenlinie lŠuft nicht mehr auf einem Kreiszylinder, sondern auf
einem Zylinder, dessen Leitlinie durch vier Ellipsenbšgen gebildet ist –
die Normalprojektion eines ãschrŠgenÒ Kreisbogens ist ja ein Ellipsenbogen. Die
zugehšrigen Ellipsen haben das AchsenverhŠltnis 
. Solche Ellipsen treten in vielen ZusammenhŠngen auf
und haben einige bemerkenswerte geometrische Eigenschaften [1]
, [2]
, [3].
Die Abbildung 8 zeigt die vier Ellipsen in extenso. Von blossem Auge ist die Innenfigur kaum von einem Kreis zu unterscheiden.
Abb. 8: Die vier Ellipsen
FŸr die Berechnung des Umfanges der Leitlinie des TrŠgerzylinders benštigen wir daher elliptische Integrale. Dies macht die Konstruktion der Abwicklung zu einer spannenden Angelegenheit.
5.4 Abwicklung
Die Abbildung 9b zeigt die Abwicklung des TrŠgerzylinders der falschen Schraubenlinie. Die falsche Schraubenlinie wird nicht auf eine Quadratdiagonale abgebildet. Ihre Steigung ist im Mittel grš§er als 1. Die Steigung ist nicht mehr konstant. Es geht wie beim Radetzky Marsch ŸberÕs Waschbrett ab.
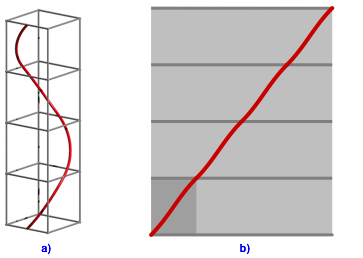
Abb. 9: Abwicklung der falschen Schraubenlinie
Die Abbildung 10 zeigt den in der Abbildung 9b etwas dunkler markierten Ausschnitt.
Am Anfang
und am Ende haben wir die Steigung 1 und den Steigungswinkel 45¡. An der
steilsten Stelle haben wir die Steigung 
und den
zugehšrigen Steigungswinkel:
(1)
Dies ist auch die Steigung einer Diagonale in einem DIN A4-Papier im Hochformat. †ber das DIN-Format siehe Walser (2013).
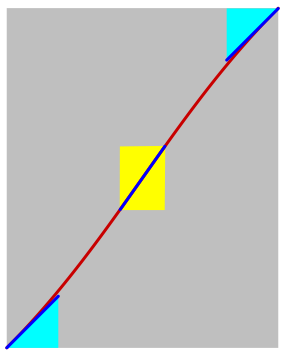
Abb. 10: Abwicklung, Ausschnitt
5.5 Torsion
Ein einzelner Bogen der falschen Schraubenlinie ist natŸrlich eine ebene Figur. Beim †bergang von einem Bogen zum nŠchsten werden die TrŠgerebenen der Bogen verdreht (Abb. 11). Wir haben eine Torsion.
Der Torsionswinkel ist der Spitzenwinkel im gleichschenkligen Dreieck der Abbildung 11. Wir erhalten:
(2)
Dieser Winkel tritt auch im kristallografischen Kontext auf. Er ist auch der Diederwinkel im regulŠren Tetraeder. Ebenso ist es der Schnittwinkel der beiden Diagonalen in einem DIN A4-Papier.
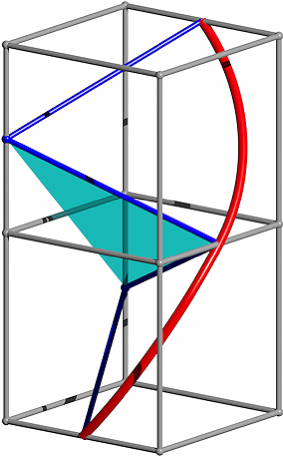
Abb. 11: Torsion
Diese sprunghafte Torsion macht die falsche Schraubenlinie als Approximation der Schraubenlinie unbrauchbar. Die Schraubenlinie muss eine konstante KrŸmmung und eine konstante Torsion haben. Sonst klemmt es beim Schrauben.
Literatur
Walser, Hans (2013): DIN A4 in Raum und Zeit. Silbernes Rechteck – Goldenes Trapez – DIN-Quader. Leipzig: EAGLE, Edition am Gutenbergplatz. ISBN 978-3-937219-69-1.
Wunder, Michael A. (2018): TreppengelŠnder und analytische Geometrie. MNU Journal 4.2018, 233-237.
Websites
[1] Hans Walser: Orthogonale Gro§kreise in isometrischer Darstellung
www.walser-h-m.ch/hans/Miniaturen/O/Orth_Grosskreise/Orth_Grosskreise.htm
[2] Hans Walser: Kreise und Ellipsen
www.walser-h-m.ch/hans/Miniaturen/K/Kreise_u_Ellipsen/Kreise_u_Ellipsen.htm
[3] Hans Walser: Rochelle-Ellipse