Hans Walser, [20100618a]

Euler-Gerade

Anregung: W. G.

1        Worum geht es?

Es werden einige geometrische Eigenschaften vorgestellt, die auf einem beliebigen Punkt auf der Euler-Geraden basieren.

2        Ein Schnittpunkt

Zwei Geraden in allgemeiner Lage schneiden sich in einem Punkt. Wenn sich aber drei Geraden in demselben Punkt schneiden, ist das bemerkenswert. Spezielle Beispiele sind die drei Hšhen eines Dreiecks oder die drei Schwerlinien oder die drei Winkelhalbierenden.

Einen weiteren Schnittpunkt kšnnen wir wie folgt finden: Wir zeichnen im Dreieck  mit dem Umkreismittelpunkt U die drei Kreise  durch  (Indizes immer aus  und modulo 3) sowie deren Mittelpunkte . Dann schneiden sich die drei Geraden  in einem gemeinsamen Punkt K. Verifikation durch DGS.

 

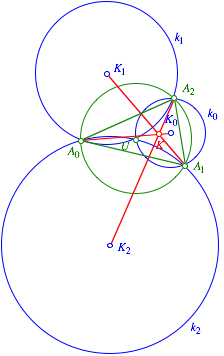
Ein Schnittpunkt

 

3        Ecktransversalen

Unter einer Ecktransversalen verstehen wir eine durch eine Dreiecksecke verlaufende Gerade. Spezielle Beispiele dazu sind Hšhen, Schwerlinien und Winkelhalbierende.

In unserem Dreieck  sei  eine durch die Ecke  verlaufende Ecktransversale.

3.1      Zuordnung eines Punktes

Zu einer beliebigen Ecktransversalen  eines Dreieckes  definieren wir einen Punkt  wie folgt: Wir zeichnen Parallelen zu  durch  und  und spiegeln diese an den Dreiecksseiten  beziehungsweise . Der Schnittpunkt der gespiegelten Gerden ist . Der Punkt  liegt im allgemeinen nicht auf der Ecktransversalen . Entsprechend kšnnend die Punkte  und  konstruiert werden.

 

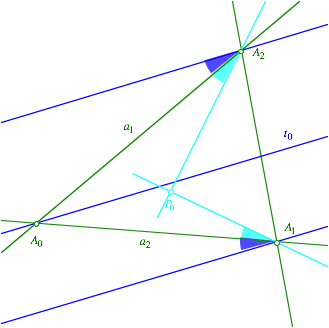
Konstruktion des Punktes

 

3.2      Vierpunkte-Kreise

Durch drei Punkte in allgemeiner Lage geht ein Kreis. Wenn aber vier Punkte auf einem Kreis liegen, ist das bemerkenswert. Das klassische Beispiel ist der Feuerbach-Kreis, auf dem sogar neun Punkte liegen.

Der Punkt  liegt auf dem Kreis  durch ,  und den Umkreismittelpunkt U. Der Kreis  ist also ein Vierpunkte-Kreis. Dies ergibt sich aus PeripheriewinkelsŠtzen. Entsprechend fźr  und .

 

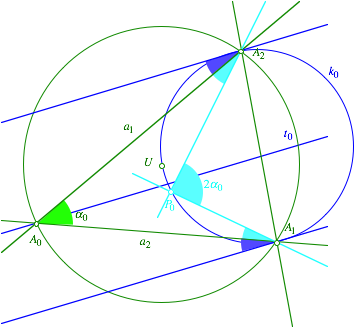
Kreis durch den Umkreismittelpunkt

 

4        Die Euler-Gerade kommt ins Spiel

Die Euler-Gerade e ist die Gerade durch den Umkreismittelpunkt U und den Hšhenschnittpunkt H. Auf ihr liegen auch der Schwerpunkt S und das Zentrum des Feuerbach-Kreises.

Fźr die folgenden Zeichnungen wŠhlen wir einen Punkt P auf der Euler-Gerade e. Wenn wir den Punkt P au§erhalb e wŠhlen, gelten die Resultate nicht.

4.1      Drei Ecktransversalen

Wir zeichnen nun drei Ecktransversalen  durch P und die zugehšrigen Punkte .  

 

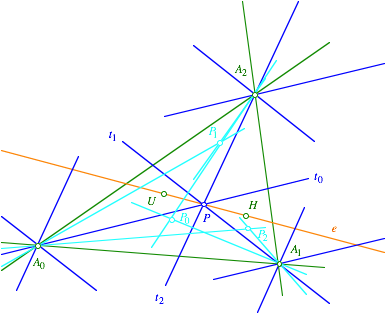
Die Euler-Gerade kommt ins Spiel

 

Im Folgenden lassen wir die Konstruktionslinien fźr die drei Punkte  weg.

 

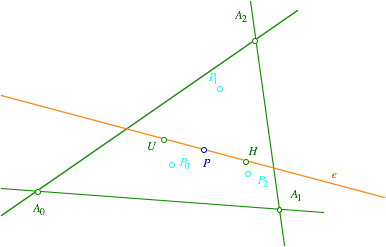
Die drei Punkte

 

4.2      Ein Vierpunkte-Kreis

Die vier Punkte  liegen auf einem Kreis. Verifikation DGS. Wenn wir P auf der Eulergeraden e bewegen, bewegt sich der Mittelpunkt dieses Kreises auf einer Hyperbel. Die Hyperbel verlŠuft durch U. Verifikation DGS.

 

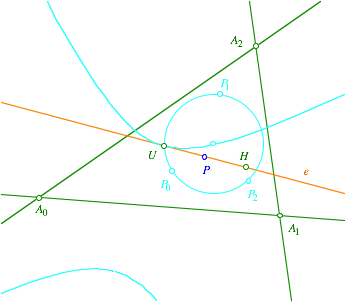
Kreis und Hyperbel

 

4.3      Ein Schnittpunkt

Die drei Geraden ,  und  verlaufen durch einen gemeinsamen Punkt. Verifikation DGS. Wenn wir P auf der Eulergeraden e bewegen, variiert dieser Punkt vermutlich auf einer Ellipse durch U.

 

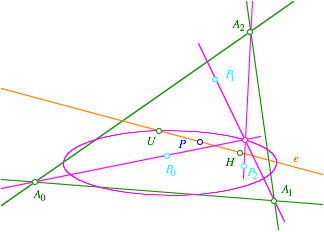
Schnittpunkt und Ellipse