Hans Walser, [20181212]
Ellipseneigenschaft
Eine Aufgabe von Thomas Jahre, Chemnitz
1 Problemstellung
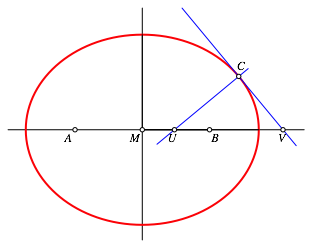
Abb. 1: Problemstellung
Eine Ellipse hat den Mittelpunkt M und die beiden Brennpunkte A und B (Abb. 1). Die Ellipsennormale und die Ellipsentangente in einem Ellipsenpunkt C schneiden die Gerade AB und U beziehungsweise V. Zu zeigen ist:
![]() (1)
(1)
Die Abbildung 2 illustriert den Sachverhalt. ZusŠtzlich sind die Strecken AC und BC eingezeichnet. Die Ellipsennormale und die Ellipsentangente sind die innere beziehungsweise Šu§ere Winkelhalbierende des Winkels ACB. Dies ist der Schlźssel fźr den Beweis von (1). Es wird sich zeigen, dass es sich um eine reine Dreiecksaufgabe handelt. Die Geschichte mit der Ellipse dient nur zur Verschleierung.
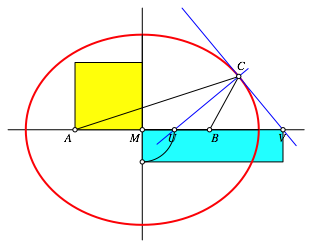
Abb. 2: Illustration
2 Randbemerkungen
Die Beziehung (1) beschreibt die Inversion am Thaleskreis źber AB (Abb. 3).
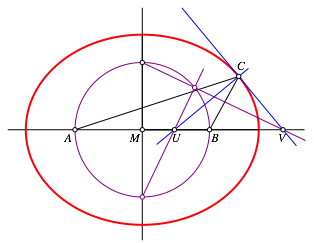
Abb. 3: Inversion am Kreis
Das Dreieck UVC ist rechtwinklig bei C. In der Abbildung 4 ist der zugehšrige Thaleskreis eingetragen.
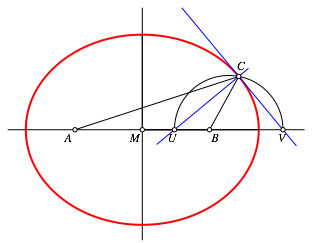
Abb. 4: Thaleskreis
Die Abbildung 2 erinnert an den Hšhensatz. In der Abbildung 5 ist das zugehšrige rechtwinklige Dreieck mitsamt Thaleskreis eingetragen.
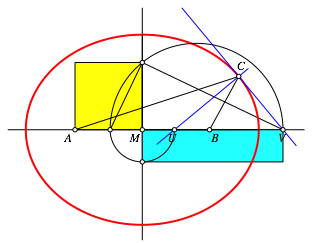
Abb. 5: Hšhensatz
Die Abbildung 6 zeigt eine †berlagerung der Abbildungen 3 bis 5.
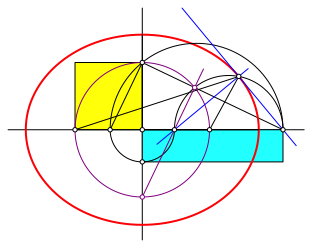
Abb. 6: †berlagerung
3 Beweis
Das Problem ist Šquivalent zu folgendem: In einem Dreieck ABC schneiden die innere und die Šu§ere Winkelhalbierende bei C die Gerade AB in U beziehungsweise V. Weiter sei M der Mittelpunkt der Strecke c = AB (Abb. 7).
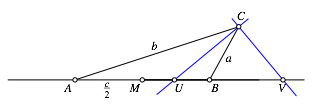
Abb. 7: Winkelhalbierende im Dreieck
Zu zeigen ist:
![]() (2)
(2)
Aus dem Satz, dass die Winkelhalbierenden die Gegenseite im VerhŠltnis der anliegenden Seiten teilen, ergibt sich:
![]() (3)
(3)
Der Rest ist Rechnung:
![]() (4)
(4)
Und damit:
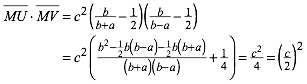 (5)
(5)
Damit sind (2) und (1) bewiesen.
Die Abbildung 8 illustriert nochmals den Sachverhalt.
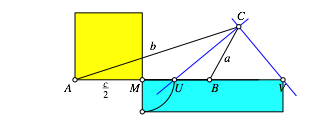
Abb. 8: Sachverhalt