Ellipse als Enveloppe von Kreisen
Inhalt
1 Zentralprojektion........................................................................................................ 1
2 Die Kugeln von
Dandelin.......................................................................................... 3
3 Sonderfall.................................................................................................................. 4
3.1 Disposition........................................................................................................ 4
3.2 Bezeichnungen................................................................................................... 6
3.3 Bilder der
Breitenkreise..................................................................................... 7
3.3.1 Kurvenschar............................................................................................... 7
3.3.2 Au§en
liegende Kreise............................................................................. 11
3.4 Bilder der
Meridiane........................................................................................ 16
3.5 Vorgehen
bei gegebener Umrissellipse............................................................ 16
1 Zentralprojektion
Wir projizieren eine Kugel mit Zentralprojektion auf eine Šquatorparallele Ebene.
Zentralprojektion der Kugel
SchrŠgbild
Sicht von oben
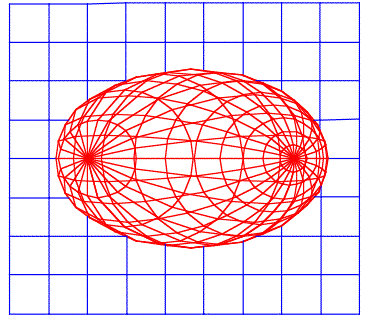
Bild der Kugel
Der Umriss des Kugelbildes ist eine Ellipse (Ellipse als Kegelschnitt).
Die Bilder der Breitenkreise sind wiederum Kreise; die Bilder der Meridiane sind Ellipsen. Die Umrissellipse kann als Enveloppe einerseits der Bilder der Breitenkreise und andererseits der Bilder der Meridiane gesehen werden.
Die Bilder von Nordpol und SŸdpol sind die Brennpunkte der Umirssellipse; wir kšnnen dies mit Hilfe der Kugeln von Dandelin beweisen.
2 Die Kugeln von Dandelin
Wenn wir die Kugel vom Projektionszentrum aus strecken, Šndert sich nichts am Kugelbild. Wir kšnnen nun zum Beispiel so strecken, dass der Nordpol oder der SŸdpol die Projektikonsebene berŸhrt. Diese beiden Kugeln sind die beiden Kugeln von Dandelin im Projektionskegel und berŸhren daher die Ellipseneben je in einem Brennpunkt.
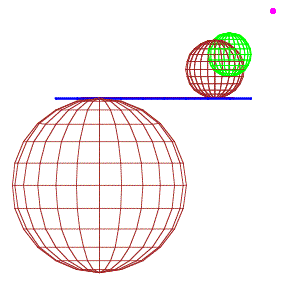
Geeignete Streckung der Urbildkugeln ergibt die Dandelinkugeln
Alle drei Kugeln haben dasselbe Bild
3 Sonderfall
3.1 Disposition
Wir denken uns das Projektionszentrum ins Unendliche verschoben, statt einer Zentralprojektion ergibt sich nun eine Parallelprojektion, welche zeichnerisch und rechnerisch einfacher zu handhaben ist. Ferner projizieren wird direkt auf die €quatorebene.
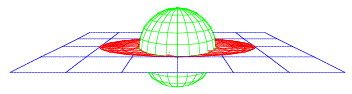
Spezielle Disposition
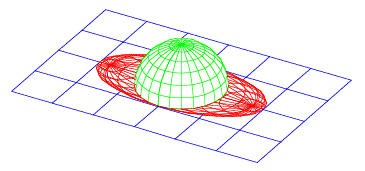
SchrŠgbild
Im Kugelbild erscheint die Umrisslinie wieder als Ellipse, die Bilder der Breitenkreise sind Kreise und die Bilder der Meridiane sind Ellipsen.
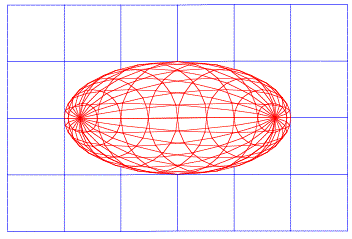
Bild der Kugel
Die Bilder der Meridiane, die Ellipsen also, berŸhren alle die Umrissellipse je in zwei diametralen Linien.
Die Bilder der Breitenkreise, welche selber Kreise sind, berŸhren aber nicht alle die Umrissellipse. Einige berŸhren die Umrissellipse in zwei Punkten, welche spiegelbildlich zur langen Ellipsenachse liegen. Dann gibt es zwei Kreise, welche die Umrissellipse genau einmal berŸhren, nŠmlich in den so genannten ãspitzenÒ Scheiteln der Ellipse, den Endpunkten der langen Ellipsenachse. Schlie§lich gibt es Kreise, welche im Innern der Ellipse liegen und den Umriss nicht berŸhren. Dies sind die Bilder von Breitenkreisen, welche ãin der NŠheÒ der Pole liegen.
3.2 Bezeichnungen
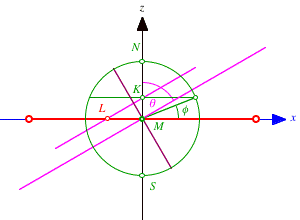
FŸr die weitere Bearbeitung sind einige Bezeichnungen praktisch. ZunŠchst bezeichnen wir den Kugelradius mit r und wie Ÿblich die lange und die kurze Halbachse der Ellipse mit a beziehungsweise b. Dann gilt zunŠchst:
Die LŠnge der langen Halbachse a hŠngt natŸrlich vom Einfallswinkel der Projektionsstrahlen
der Parallelprojektion ab. Wir bezeichnen den Winkel zwischen diesen Strahlen
und der Erdachse mit 
.
Schlie§lich fŸhren wir ein kartesisches Koordinatensystem ein mit dem Ursprung im Kugelmittelpunkt und der z-Achse auf der Erdachse. Die Projektionsstrahlen sollen parallel zur x,z-Ebene liegen.
Es seien die beiden Brennpunkte 
und 
die Bilder des
SŸdpols S beziehungsweise des Nordpols N.
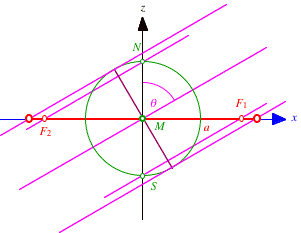
Bezeichnungen und Koordinatensystem
Mit diesen Bezeichnungen fŸr die lange Halbachse:
Die Brennpunkte haben die Koordinaten 
mit 
.
Somit ist:
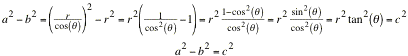
Der Gro§kreis auf der Kugel, dessen Ebene senkrecht zur Projektionsrichtung steht, ist das Urbild der Umrissellipse bei der Projektion.
3.3 Bilder der Breitenkreise
Der Breitenkreis zur geografischen Breite 
hat den Radius 
. Sein Mittelpunkt K
hat die Koordinaten 
. Das Bild dieses Breitenkreises hat ebenfalls den
Radius 
; fŸr das Bild L von
K erhalten wir 
.
Breitenkreis
3.3.1 Kurvenschar
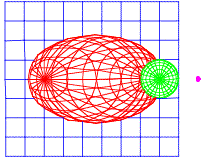
Die Kurvenschar
mit dem Scharparameter 
beschreibt also
die Bilder der Breitenkreise. In der folgenden Figur ist 
und 
.
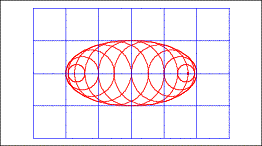
Kurvenschar
In der folgenden Figur ist 
und 
.
Kurvenschar, kleinerer Schritt
Wenn wir in den Netzvierecken ãhorizontaleÒ Diagonalen einzeichnen, entsteht eine Schar von konfokalen Ellipsen, zu der auch die Umrissellipse gehšrt.
Die Fresse ist offen
Es versteht sich von selbst, dass wir bei den ãvertikalenÒ Diagonalen eine Schar von konfokalen Hyperbeln mit denselben Brennpunkten wie die Umrissellipse erhalten.
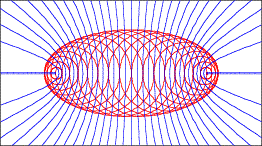
Konfokale Hypberbelschar
3.3.1.1 Drei FŠlle
Wir haben schon festgestellt, dass einige Kreise die
Umrissellipse zwei Mal berŸhren; das sind die Kreise fŸr 
. Die zugehšrigen Breitenkreise schneiden das Urbild der
Umrissellipse zwei Mal.
Im Grenzfall 
erhalten wir
zwei Breitenkreise, welche das Urbild der Umrissellipse berŸhren; die Bilder
dieser Breitenkreise sind die KrŸmmungskreise an die Ellipse in den beiden
spitzen Scheiteln. Diese beiden KrŸmmungskreise haben also den Radius 
. Dabei gilt folgende Beziehung:
Wir kšnnen also den Radius dieser KrŸmmungskreise durch die Halbachsen ausdrŸcken.
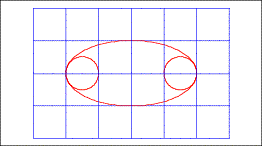
KrŸmmungskreise
FŸr 
schlie§lich
berŸhren die Kreise die Umrissellipse nicht.
3.3.1.2 BerŸhrpunkte
In welchen beiden Punkten berŸhren die Kreise fŸr 
die
Umrissellipse?
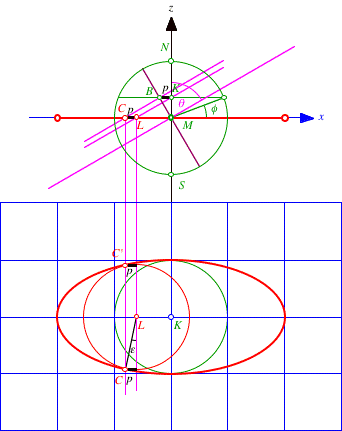
BerŸhrpunkte?
FŸr die eingezeichnete Strecke p finden wir aus der oberen Figur:
Daraus ergibt sich fŸr den eingezeichneten Winkel 
:
Damit lassen sie die BerŸhrungspunkte berechnen. Sie haben
die Koordinaten 
.
3.3.2 Au§en liegende Kreise
Die Idee ist nun, zu zwei symmetrischen innen liegenden Kreisen zwei au§en liegende Kreise zu finden, welche die Ellipse in denselben Punkten berŸhren.
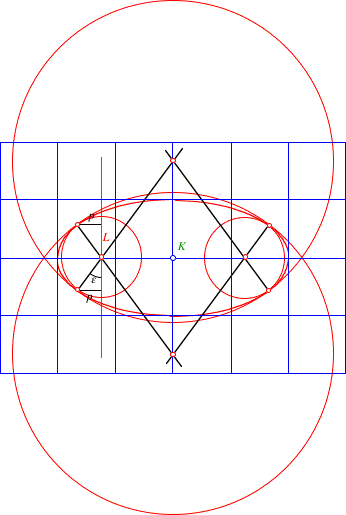
Au§en liegende Kreise
3.3.2.1 Korbbogen
Wenn wir von den vier Kreisen nur geeignete Bšgen nehmen, erhalten wir eine Approximation der Ellipse durch einen so genannten Korbbogen. Diese Approximation ist in den vier BerŸhrpunkten exakt, auch mit exakter Tangente.
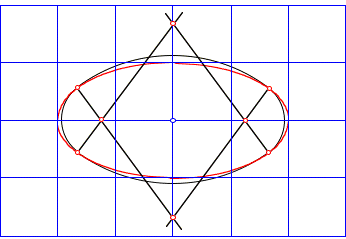
Approximation der Ellipse durch einen Korbbogen
3.3.2.2 Schar von au§en liegenden Kreisen
Nach einiger Rechung erhŠlt man fŸr die au§en liegenden Kreise die Radien:
FŸr die Schar au§en liegender Kreise ergibt sich die Parameterdarstellung:
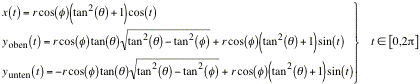
Wegen dem Wurzelausdruck besteht fŸr den Scharparameter 
die Bedingung:
Die folgende Figur zeigt die Situation fŸr 
und 
.
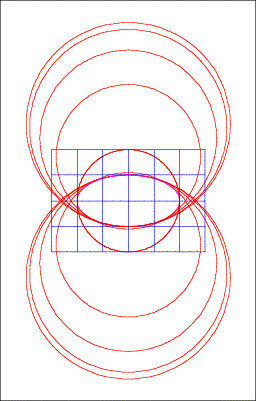
Kurvenschar
Die Umrissellipse erscheint als innere Enveloppe der Kreisschar.
Die folgende Figur zeigt die Situation fŸr 
und 
.
Kleinerer Schritt
3.3.2.3 KrŸmmungskreisee
FŸr 
ergibt sich der
Radius 
. Dabei gilt die Beziehung:
Wir erhalten fŸr 
die
KrŸmmungskreise an den so genannten stumpfen Scheiteln der Ellipse.
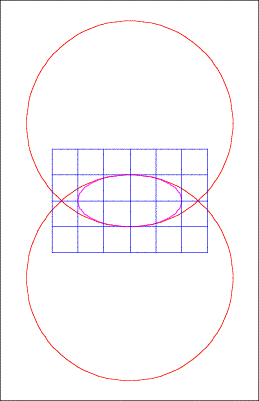
KrŸmmungskreise in den stumpfen Scheiteln
3.4 Bilder der Meridiane
Die Kurvenschar
mit dem Scharparameter 
beschreibt die
Bilder der Meridiane. In der folgenden Figur ist 
und 
.
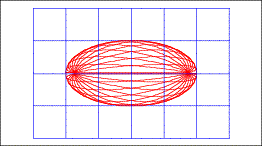
Ellipsenschar
3.5 Vorgehen bei gegebener Umrissellipse
Es seien a und b die Halbachsen der vorgegebenen Umrissellipse.
Dann ist 
und 
, also 
. Daraus ergibt sich:
Die Parameterdarstellung
beschreibt bei festem 
das Bild eines
Breitenkreises, also einen Kreis, und bei festem 
das Bild eines
Meridians, also eine (halbe) Ellipse.